Собственные электрические колебания в колебательном контуре. Логарифмический декремент затухания и добротность колебания
Колебания электрических величин — заряда, напряжения, тока — можно наблюдать в цепи, состоящей из последовательно соединённых сопротивления (R), ёмкости (C) и катушки индуктивности (L)
Колебания, происходящие только за счёт внутренних энергетических ресурсов системы, называются собственными. Первоначально энергия была сообщена конденсатору и локализована в электростатическом поле. При замыкании конденсатора на катушку, в цепи появляется разрядный ток, а в катушке — магнитное поле. Э.д.с. самоиндукции катушки будет препятствовать мгновенной разрядке конденсатора. Через четверть периода конденсатор полностью разрядится, но ток будет продолжать течь, поддерживаемый электродвижущей силой самоиндукции. К моменту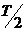 
эта э.д.с. перезарядит конденсатор. Ток в контуре и магнитное поле уменьшатся до нуля, заряд на обкладках конденсатора достигнет максимального значения.
Эти колебания электрических величин в контуре будут происходить неограниченно долго, если сопротивление контура R = 0. Такой процесс называют собственные незатухающие колебания.
Если сопротивлением резистора R (силой сопротивления в механическом осцилляторе) пренебречь нельзя, то в подобных системах будут происходить собственные затухающие колебания.
Характер затухающих колебаний меняется с увеличением сопротивления резистора R. Когда сопротивление превысит определённое критическое значение Rк, колебания в системе не возникают. Происходит монотонный апериодический разряд конденсатора
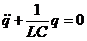. Это линейное дифференциальное уравнение второго порядка — дифференциальное уравнение собственных незатухающих электрических колебаний. Решением этого уравнения является следующая гармоническая функция: q = Acos(w0t + j). частота собственных незатухающих колебаний гармонического осциллятора: 
.
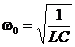Окончательно закон изменения заряда конденсатора во времени принимает следующий вид:
q = q0cos(w0t). Ток в цепи при этом меняется так: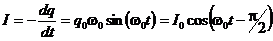 
Собственные затухающие колебания происходят в колебательном контуре RLC
Эти колебания можно описать следующим дифференциальным уравнением (правило напряжений Кирхгофа): IR – UC = eСИ.Здесь по-прежнему: I =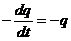 
; UC = 
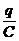; eСИ = 
= 
= 
.
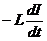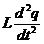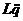Учитывая эти соотношения, уравнению придадим следующий вид:
; 
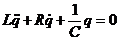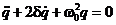(11.7). есь d = 
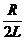— коэффициент затухания; 
= 
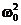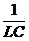— частота собственных незатухающих колебаний. Уравнение 11.7— дифференциальное уравнение собственных затухающих электрических колебаний.
Важной характеристикой затухающего процесса является логарифмический декремент затухания — логарифм отношения амплитуд двух соседних колебаний :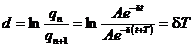 
. Логарифмический декремент затухания равен произведению коэффициента затухания d на время одного полного колебания (период) Т. Процесс затухания колебания до нуля продолжается бесконечное время, поэтому условно принято считать, что процесс затух, если амплитуда колебаний уменьшилась в е раз.
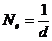и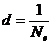 
.
Логарифмический декремент затухания d обратен числу колебаний, по истечению которых амплитуда падает в е раз. В радиотехнике для энергетической характеристики затухания часто используют величину, которая получила название добротность контура: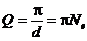 
.