Закон сохранения полной механической энергии

Векторный способ

в векторном способе положение материальной точки задаёт радиус-вектор r
радиус-вектор – вектор, соединяющий начало координат системы отсчета и положение точки в данный момент времени t

радиус-вектор выражается через проекции этого вектора на соответствующие оси координат

r = xe_x + ye_y + ze_z

уравнение движения в векторной форме

r = r(t) = {x(t), y(t), z(t)}

Координатный способ

в этом способе с выбранным телом отсчета жестко связывают определённую систему координат. Положение точки характеризуют три проекции радиус-вектора

x = x(t), y = y(t), z = z(t)

«естественный» способ

этот способ описания движения используется когда заранее известна траектория точки. Положение точки определяют дуговой координатой – расстоянием вдоль траектории от выбранного начала отсчета О.

Траектория – линия, которую описывает тело при своем движении. (геометрическое место концов радиус-вектора)

Путь – длина траектории, пройденной телом за определённый промежуток времени.

Перемещение – вектор, соединяющий два последовательных положения точки на траектории.

Средняя скорость перемещения – отношение перемещения dr к промежутку времени dt, за которое произошло приращение радиус-вектора

Средняя путевая скорость – отношение пройденного пути к интервалу времени

Мгновенная скорость – физ величина, характеризующая быстроту изменения радиус-вектора со временем и направление движения материальной точки и определяемая как первая производная радиус-вектора.

Среднее ускорение – физ величина, характеризующая быстроту изменения скорости с течением времени по модулю и направлению.

Мгновенное ускорение - -||-

Вращательное движениематериальной точки в общем случае можно определить как движение её по замкнутой траектории.

Мгновенная скорость тела при криволинейном движении направлена в любой точке траектории по касательной к траектории в этой точке.

Ускорения при криволинейном движении всегда направлены в сторону вогнутости траектории (центростремительное ускорение).

Прямая задача кинематики заключается в определении кинематических характеристик движения по заданному уравнению движения путём дифференцирования радиус-вектора по времени для определения скорости или путем дифференцирования скорости по времени для нахождения ускорения

Обратная задача кинематики сводится к определению скорости и уравнения движения по заданному ускорению.

Первый закон Ньютона

Существую такие системы отсчета относительно которых тело сохраняет состояние покоя или равномерное и прямолинейное движение, пока внешнее воздействие не выведет его из этого состояния.

Системы отсчета, в которых свободное тело покоится или движется прямолинейно и равномерно наз. инерциальными.

Сила – физическая величина, определяющая общую меру различных видов механического взаимодействия между телами, в результате чего тела деформируются или приобретают ускорение.

Если с рассматриваемой частицей взаимодействуют сразу несколько других частиц, то каждое из парных взаимодействий не искажается другими взаимодействиями и, следовательно, результирующая сила, действующая на данную частицу, равна векторной сумме сил, связанных со всеми её парными взаимодействиями в отдельности.

Масса – мера инертности тела.

Импульс тела– динамическая характеристика движения.

Второй закон Ньютона

Равнодействующая сил, действующих на данное тело равна произведению массы тела на его ускорение.

Третий закон Ньютона

Силы взаимодействия двух материальных точек в инерциальной системе отсчета равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей точки.

Система тел – совокупность тел, выделенная для рассмотрения, т.е. совокупность тел, движение которых необходимо описать.

Закон сохранения импульса

Векторная (геометрическая) сумма импульсов замкнутой системы материальных точек сохраняется, т.е. не изменяется со временем.

Работа силы - мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения.

Мощность– физическая величина, равная отношению работы ко времени, за которое была совершена эта работа.

Энергия – общая мера всех форм движения.

Кинетическая энергия– это часть полной энергии, характеризующая движение.

Силовое поле – часть пространства (ограниченная или неограниченная), в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила, зависящая или только от координат x, y, z этой точки, или же от координат x, y, z и времени t.

Консервативные силы– силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил).

Потенциальная энергия - часть полной механической энергии системы, зависящая от взаимного расположения частиц, составляющих эту систему, и от их положений во внешнем силовом поле.

Градиент скалярной функции –вектор, направленный в сторону максимально быстрого возрастания этой функции и численно равный скорости её возрастания в указанном направлении.

Связь силы с потенциальной энергией – сила равна градиенту потенциальной энергии, взятого с обратным знаком.

Работа консервативной силы равна изменению потенциальной энергии частицы, взятому с обратным знаком.

Полная механическая энергия -сумма кинетической и потенциальной энергии тела.

Теорема Штейнера

Момент инерции тела J_zO относительно произвольной оси равен сумме его момента инерции J_zC относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния d между осями.

J_zO = J_zC + md²

Момент импульса твердого тела относительно оси – сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси.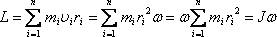

Взаимосвязь энергии и массы

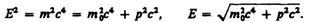
при U = 0 полная энергия называется энергией покоя тела W₀:

W₀ = mc²

Энергия покоя представляет собой внутреннюю энергию частицы или тела, не связанную с движением тела как целого и его взаимодействием с внешними силовыми полями.

Потенциальная энергия частиц во внешнем поле в энергию покоя W₀ не включается, так же как и в полную энергию W.

Полная энергия – сумма энергии покоя и кинетической энергии.

Кинетическая энергия тела определяется как разность между полной энергией и энергией покоя:

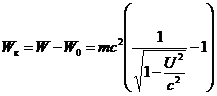
Закон Гука

Относительное растяжение (сжатие) ε пропорционально растягивающему (сжимающему) напряжению d

d = E ε

E – коэффициент пропорциональности (модуль Юнга)

Способ Лагранжа

Способ эквивалентен обычному кинематическому описанию движения частиц. Выбирается совокупность «жидких» частиц, и движение жидкости описывается как движение таких частиц. При этом вводятся понятия скорости и ускорения частиц. Способ Лагранжа редко применяется при решении гидродинамических задач. Это связано с осложнениями из-за того, что форма «жидкой» частицы в процессе движения может изменяться самым причудливым образом и это трудно учесть в теории.

Используя способ Лагранжа, мы следим за поведением отдельных «жидких» частиц, отмечая их кинематические характеристики в последовательные моменты времени в разных точках пространства, через которые проходят частицы в процессе своего движения.

Способ Эйлера.

Способ является общеупотребительным при описании движения жидкости. Он заключается в задании векторного поля скоростей движения жидкости. Иными словами, мы изучаем зависимости скорости движения жидкости от координат и времени: U_x = U_x (x, y, z, t), U_y = U_y (x, y, z, t), U_z = U_z (x, y, z, t), т.е. фиксируем как ведёт себя скорость течения жидкости в точках её объема с течением времени.

Используя способ Эйлера, мы следим за кинематическими характеристиками жидкости в фиксированных точках пространства, не интересуясь тем, какие именно «жидкие» частицы проходят через эти точки.

Уравнение непрерывности

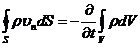
Уравнение движения жидкости

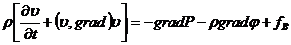
Уравнение Бернулли

В установившемся движении идеальной жидкости полное давление, слагающееся из динамического, гидростатического и статического, одинаково для всех поперечных сечений трубки тока.

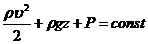
Молекулярно-кинетическая теория (МКТ)устанавливает связи между макро- и микропараметрами идеального газа. Основное уравнение МКТ выражает связь давления газа со средней кинетической энергией поступательного движения молекул.

Формулировка

давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Макроскопические параметры

- количество вещества

- объем

- температура

- давление

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

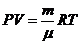
Число степеней свободы

Число степеней свободы – наименьшее число независимых координат, определяющих положение и конфигурацию молекулы в пространстве

Число степеней свободы:

- для одноатомной молекулы -3 (поступательное движение в направлении трех координатных осей),

- для двухатомной - 5 ( три поступательных и две вращательных, т.к. вращение вокруг оси Х возможно только при очень высоких температурах),

- для трехатомной -6 ( три поступательных и три вращательных).

теорема о равнораспределении кинетической энергии по степеням свободы позволяет связать температуру системы с её средней энергией.

Содержание теоремы:

на все степени свободы статистической системы приходится одна и та же энергия .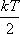

Изобарический процесс

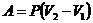
Изотермический процесс

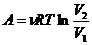
Изохорический процесс

Первое начало термодинамики

Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии.

Формулировка:

1. теплота, переданная системе, и работа, совершенная над системой, направлены на изменение внутренней энергии системы
2. при переходе системы между двумя состояниями изменение внутренней энергии не зависит от вида процесса, посредством которого произведен этот переход.

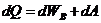
Изобарический процесс

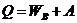
Изохорический процесс

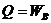
Изотермический процесс

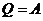
Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температуры δT, которое при этом произошло

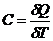
Тепловая машина

Тепловые машины подразделяются на тепловые двигатели и холодильные установки. Работа тепловой машины может быть сведена к взаимодействию трех элементов: нагревателя, холодильника и рабочего тела. Тепловые двигатели предназначены для преобразования теплоты в работу.

При выполнении цикла рабочее тело получает от нагревателя теплоту Q₁, отдаёт холодильнику теплоту Q₂ и разность этих теплот преобразует в полезную работу
A = Q₁ – Q₂

Эффективность двигателя характеризуется его коэффициентом полезного действия, определяемым как отношение полезной работы к полученной теплоте:

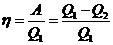
Холодильные установки предназначены для производства холода. При выполнении цикла рабочее тело забирает от холодильника теплоту Q₂, получает из внешней среды работу A и передаёт нагревателю теплоту Q₁ = Q₂ + A

Цикл Карно

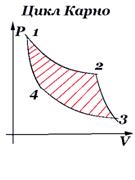Состоит из двух изотерм и двух адиабат. В двигателе этот цикл проходит по часовой стрелке, в холодильной установке – в противоположном направлении. В точке 1 рабочее тело приводится в контакт с нагревателем и, находясь в этом контакте, изотермически расширяется при температуре T₁ до состояния 2. При этом от нагревателя забирается теплота и совершается положительная работа расширения. В точке 2 прекращается контакт с нагревателем и рабочее тело адиабатически расширяется до состояния 3. При этом совершается положительная работа, убывает внутренняя энергия и уменьшается температура тела. В точке 3 рабочее тело приводится в контакт с холодильником и, находясь в этом контакте, изотермически сжимается действием внешних сил при температуре T₂. При этом совершается отрицательная работа сжатия и холодильнику передаётся часть полученной от нагревателя теплоты. В точке 4 прекращается контакт с холодильником и рабочее тело адиабатически сжимается действием внешних сил до исходного состояния 1. При этом совершается отрицательная работа сжатия и увеличивается внутренняя энергия и температура тела.

КПД цикла Карно

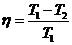
Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Формулировки

Существуют несколько эквивалентных формулировок второго начала термодинамики:

- Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему»[1] (такой процесс называется процессом Клаузиуса).

- Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

- «Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Энтропией называется функция состояния, изменение которой при обратимом переходе между состояниями выражается как интеграл 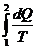, взятый по любой кривой, характеризующей обратимый переход между этими состояниями.

Свойства энтропии:

1. Энтропия изолированной системы при протекании необратимого процесса возрастает.

2. Энтропия системы, находящейся в равновесном состоянии, максимальна.

Векторный способ

в векторном способе положение материальной точки задаёт радиус-вектор r
радиус-вектор – вектор, соединяющий начало координат системы отсчета и положение точки в данный момент времени t

радиус-вектор выражается через проекции этого вектора на соответствующие оси координат

r = xe_x + ye_y + ze_z

уравнение движения в векторной форме

r = r(t) = {x(t), y(t), z(t)}

Координатный способ

в этом способе с выбранным телом отсчета жестко связывают определённую систему координат. Положение точки характеризуют три проекции радиус-вектора

x = x(t), y = y(t), z = z(t)

«естественный» способ

этот способ описания движения используется когда заранее известна траектория точки. Положение точки определяют дуговой координатой – расстоянием вдоль траектории от выбранного начала отсчета О.

Траектория – линия, которую описывает тело при своем движении. (геометрическое место концов радиус-вектора)

Путь – длина траектории, пройденной телом за определённый промежуток времени.

Перемещение – вектор, соединяющий два последовательных положения точки на траектории.

Средняя скорость перемещения – отношение перемещения dr к промежутку времени dt, за которое произошло приращение радиус-вектора

Средняя путевая скорость – отношение пройденного пути к интервалу времени

Мгновенная скорость – физ величина, характеризующая быстроту изменения радиус-вектора со временем и направление движения материальной точки и определяемая как первая производная радиус-вектора.

Среднее ускорение – физ величина, характеризующая быстроту изменения скорости с течением времени по модулю и направлению.

Мгновенное ускорение - -||-

Вращательное движениематериальной точки в общем случае можно определить как движение её по замкнутой траектории.

Мгновенная скорость тела при криволинейном движении направлена в любой точке траектории по касательной к траектории в этой точке.

Ускорения при криволинейном движении всегда направлены в сторону вогнутости траектории (центростремительное ускорение).

Прямая задача кинематики заключается в определении кинематических характеристик движения по заданному уравнению движения путём дифференцирования радиус-вектора по времени для определения скорости или путем дифференцирования скорости по времени для нахождения ускорения

Обратная задача кинематики сводится к определению скорости и уравнения движения по заданному ускорению.

Первый закон Ньютона

Существую такие системы отсчета относительно которых тело сохраняет состояние покоя или равномерное и прямолинейное движение, пока внешнее воздействие не выведет его из этого состояния.

Системы отсчета, в которых свободное тело покоится или движется прямолинейно и равномерно наз. инерциальными.

Сила – физическая величина, определяющая общую меру различных видов механического взаимодействия между телами, в результате чего тела деформируются или приобретают ускорение.

Если с рассматриваемой частицей взаимодействуют сразу несколько других частиц, то каждое из парных взаимодействий не искажается другими взаимодействиями и, следовательно, результирующая сила, действующая на данную частицу, равна векторной сумме сил, связанных со всеми её парными взаимодействиями в отдельности.

Масса – мера инертности тела.

Импульс тела– динамическая характеристика движения.

Второй закон Ньютона

Равнодействующая сил, действующих на данное тело равна произведению массы тела на его ускорение.

Третий закон Ньютона

Силы взаимодействия двух материальных точек в инерциальной системе отсчета равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей точки.

Система тел – совокупность тел, выделенная для рассмотрения, т.е. совокупность тел, движение которых необходимо описать.

Закон сохранения импульса

Векторная (геометрическая) сумма импульсов замкнутой системы материальных точек сохраняется, т.е. не изменяется со временем.

Работа силы - мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения.

Мощность– физическая величина, равная отношению работы ко времени, за которое была совершена эта работа.

Энергия – общая мера всех форм движения.

Кинетическая энергия– это часть полной энергии, характеризующая движение.

Силовое поле – часть пространства (ограниченная или неограниченная), в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила, зависящая или только от координат x, y, z этой точки, или же от координат x, y, z и времени t.

Консервативные силы– силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил).

Потенциальная энергия - часть полной механической энергии системы, зависящая от взаимного расположения частиц, составляющих эту систему, и от их положений во внешнем силовом поле.

Градиент скалярной функции –вектор, направленный в сторону максимально быстрого возрастания этой функции и численно равный скорости её возрастания в указанном направлении.

Связь силы с потенциальной энергией – сила равна градиенту потенциальной энергии, взятого с обратным знаком.

Работа консервативной силы равна изменению потенциальной энергии частицы, взятому с обратным знаком.

Полная механическая энергия -сумма кинетической и потенциальной энергии тела.

Закон сохранения полной механической энергии

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.