Движение тела переменной массы.Реактивное движение.

Механика тел переменной массы-раздел теоретической механики, в котором изучаются движения материальных тел, масса которых изменяется во время движения. Основоположники Механика тел переменной массы — И. В. Мещерский и К. Э. Циолковский. Изменение массы тела (точки) во время движения может обусловливаться отделением (отбрасыванием) частиц или их присоединением (налипанием). Основное векторное дифференциальное уравнение движения точки переменной массы для случая присоединения и отделения частиц (впервые полученное в 1904 Мещерским) имеет вид:

ma=F+F_P,где F_P-реактивная сила

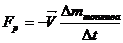
Реактивное движение - движение тела, обусловленное отделением от него с некоторой скоростью какой-то его части.

Все виды движения, кроме реактивного, невозможны без наличия внешних для данной системы сил, т. е. без взаимодействия тел данной системы с окружающей средой, а для осуществления реактивного движения не требуется взаимодействия тела с окружающей средой. Первоначально система покоится, т. е. ее полный импульс равен нулю. Когда из системы начинает выбрасываться с некоторой скоростью часть ее массы, то (так как полный импульс замкнутой системы по закону сохранения импульса должен оставаться неизменным) система получает скорость, направленную в противо-положную сторону. Действительно, так как m₁v₁+m₂v₂=0, то m₁v₁=-m₂v₂, т. е.

v₂=-v₁m₁/m₂.

8.Постулаты специальной теории относительности.Преобразования Лоренца и следствия из них:относительность одновременности,промежутков времени и длин.

Специа́льная тео́рия относи́тельности (СТО)- теория, описывающая движение, законы механики и пространственно-временные отношения, определяющие их, при скоростях движения, близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей образует общую теорию относительности.

СТО полностью выводится на физическом уровне строгости из трёх постулатов (предположений):

1.Справедлив принцип относительности Эйнштейна — расширение принципа относительности Галилея. (все физ. процессы в ИСО протекают одинаково)

2.Скорость света не зависит от скорости движения источника во всех инерциальных системах отсчёта.

3.Пространство и время однородны, пространство является изотропным.

Преобразованиями Лоренца в физике, в частности в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты (x,y,z,t) каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой. Аналогично преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.

Классические преобразования Галилея несовместимы с постулатами СТО и, следовательно, должны быть заменены. Эти новые преобразования должны установить связь между координатами (x, y, z) и моментом времени t события, наблюдаемого в системе отсчета K, и координатами (x', y', z') и моментом времени t' этого же события, наблюдаемого в системе отсчета K'.Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:

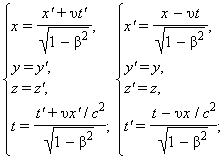
Из преобразований Лоренца вытекает целый ряд следствий. В частности, из них следует релятивистский эффект замедления времени и лоренцево сокращение длины. Пусть, например, в некоторой точке x' системы K' происходит процесс длительностью τ0 = t'2 – t'1 (собственное время), где t'1 и t'2 – показания часов в системе K' в начале и конце процесса. Длительность τ этого процесса в системе K будет равна

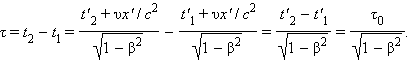
Аналогичным образом, можно показать, что из преобразований Лоренца вытекает релятивистское сокращение длины. Одним из важнейших следствий из преобразований Лоренца является вывод об относительности одновременности. Пусть, например, в двух разных точках системы отсчета K' (x'1 ≠ x'2) одновременно с точки зрения наблюдателя в K' (t'1 = t'2 = t') происходят два события. Согласно преобразованиям Лоренца, наблюдатель в системе K будет иметь

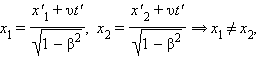
Следовательно, в системе K эти события, оставаясь пространственно разобщенными, оказываются неодновременными. Более того, знак разности t2 – t1 определяется знаком выражения υ(x'2 – x'1), поэтому в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшествует первому. Этот вывод СТО не относится к событиям, связанным причинно-следственными связями, когда одно из событий является физическим следствием другого. Можно показать, что в СТО не нарушается принцип причинности, и порядок следования причинно-следственных событий одинаков во всех инерциальных системах отсчета.