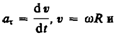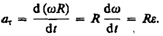Уравнение поступательного движения материальной точки.

Линейная скорость точки

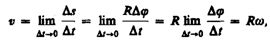
Если ( 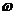= const, то вращение равномерное и его можно характеризовать периодомвращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени Dt = T соответствует 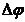=2p, то 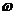=2p/T, откуда

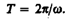
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

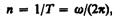
откуда

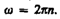
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

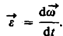
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 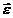сонаправлен вектору 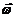(рис.8), при замедлен­ном — противонаправлен ему (рис.9).

Тангенциальная составляющая ускорения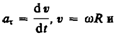

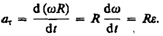
Полная механическая энергия. Закон сохранения механической энергии. Работа в замкнутой системе и работа под действием внешних сил.

1. Полная механическая энергия. Закон сохранения механической энергии.

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии взаимодействия этих тел друг с другом и с внешними телами:

Е = Е_к+ Е_п.

Закон сохранения механической энергии: механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.

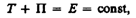
2.Работа в замкнутой системе и работа под действием внешних сил.

Замкнутая система тел в механике — совокупность физических тел, у которых взаимодействия с внешними телами отсутствуют. В этой системе работа равна нулю.

Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил :

Авн = ΔЕ = Е – Е0, (20)

где Е и Е0 – полные механические энергии системы в конечном и начальном состояниях соответственно.

Теорема Гюйгенса-Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

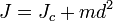
Если 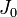— момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии 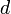от неё, равен

,

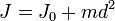где 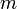— полная масса тела.

Поверхностная энергия и натяжение. Капиллярные явления.

Поверхностная энергия

Молекулы поверхностного слоя жидкости обладают дополнительной потенциальной энергией по сравнению с молекулами внутри жидкости. Эту энергию называют поверхностной энергией. Величина поверхностной энергии тем больше, чем больше площадь свободной поверхности

.

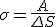Единицей коэффициента поверхностного натяжения в СИ является джоуль на квадратный метр (Дж/м²).

Поверхностное натяжение

Равнодействующая сил, действующих на все молекулы, находящиеся на границе свободной поверхности, и есть сила поверхностного натяжения. В целом она действует так, что стремится сократить поверхность жидкости.

.

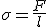Согласно этой формуле единицей коэффициента поверхностного натяжения в СИ является ньютон на метр (Н/м).

Коэффициент поверхностного натяжения σ численно равен силе поверхностного натяжения, действующей на единицу длины границы свободной поверхности жидкости. Коэффициент поверхностного натяжения зависит от природы жидкости, от температуры и от наличия примесей. При увеличении температуры он уменьшается.

Капиллярные явления, физические явления, обусловленные действием поверхностного натяжения на границе раздела несмешивающихся сред. К К. я. относят обычно явления в жидких средах, вызванные искривлением их поверхности, граничащей с др. жидкостью, газом или собственным паром. Искривление поверхности ведёт к появлению в жидкости дополнительного капиллярного давления Dp, величина которого связана со средней кривизной r поверхности уравнением Лапласа: Dp = p₁— p₂. = 2s₁₂/r, где (s₁₂ — поверхностное натяжение на границе двух сред; p₁ и p₂— давления в жидкости 1 и контактирующей с ней среде.

Статические и термодинамические методы исследования вещества. Состояние, процесс, термодинамические параметры. Термодинамическое решение. Модель идеального газа. Газовые законы. Основное уравнение молекулярно-кинетической теории.

Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конеч­ном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц. Термодинамика не рассматривает микропроцессы, кото­рые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных за­конах, установленных в результате обобщения опытных данных.

Переход из одного термодинамического состояния в другое называется термодинамическим процессом. Равновесным состоянием - состоянием термодинамического равновесия - называется такое состояния термодинамической системы, в котором отсутствуют всякие потоки (энергии, вещества, импульса и т. д.), а макроскопические параметры системы являются установившимися и не изменяются во времени. Если какая-либо термодинамическая система находится в термодинамическом равновесии с двумя другими системами, то и эти две системы находятся в термодинамическом равновесии друг с другом.

Модель идеального газа

1. Число молекул в газе велико: N>> 1, среднее расстояние между отдельными молекулами много больше их размеров (l>>a).
2. Молекулы газа совершают неупорядоченное, хаотическое движение.
3. Движение отдельных молекул подчиняется законам механики, молекулы рассматриваются как материальные точки, совершающие только поступательное движение. Величина потенциальной энергии взаимодействия мала по сравнению со средней кинетической энергией.
4. Все соударения молекул друг с другом и со стенками сосуда, в котором находится газ, являются абсолютно упругими При ударе о стенку компонента импульса молекулы, перпендикулярная стенке, меняет знак. Выполняются законы сохранения импульса и энергии для молекул газа.

Произведение давления идеального газа на его объем пропорционально плотности числа молекул в газе и средней кинетической энергии поступательного движения отдельной молекулы,т.е.

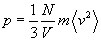
Изотермический процесс. Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре .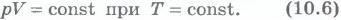

Изобарный процесс. Процесс изменения состояния термодинамической системы при постоянном давлении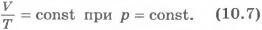

Изохорный процесс. Процесс изменения состояния термодинамической системы при постоянном объеме.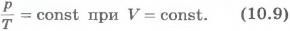

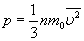-основное уравнение мкт.

Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа 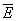: 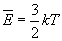, получим .

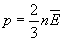Паровой двигатель

Это двигатель, приводимый в действие силой пара. Пар, получаемый путем нагрева воды, используют для движения. В некоторых двигателях сила пара заставляет двигаться поршни, расположенные в цилиндрах. Т.о. создается возвратно-поступательное движение. Подсоединенный механизм обычно преобразует его во вращательное движение. В паровозах (локомотивах) используются поршневые двигатели. В качестве двигателей используют также паровые турбины, которые дают непосредственно вращательное движение, вращая ряд колес с лопатками. Паровые турбины приводят в действие генераторы электростанций и винты кораблей. В любом паровом двигателе происходит превращение тепла, вырабатываемого при нагреве воды в паровом котле (бойлере) в энергию движения. Тепло может подаваться от сжигания топлива в печи или от атомного реактора.

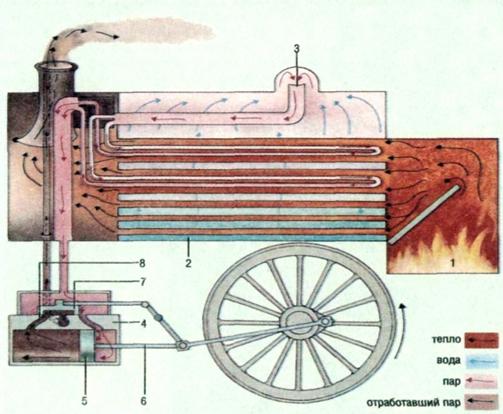
Паровые двигатели, такие как раньше использовались в локомотивах, работают на производимом при нагревании воды паре. Угольная или дровяная топка (1) нагревает котел, напол-ненный водой (2), который производит пар. Пар поднимается и через сухопарник(3) выталкивается через трубы в цилиндр (4), где он вызывает обратное движение поршня (5). Связанный с поршнем рычаг (6) это золотниковый клапан (7), который сначала позволяет пару попасть в цилиндр (как показано), закрывая выпускное окно (8). Это создает давление, которое двигает поршень вперед и приводит к тому, что золотниковый клапан становится в такое положение, когда выпускное окно открывается и пар выходит наружу. Движение колес заставляет поршень двигаться назад, и все начинается снова.

Уравнение поступательного движения материальной точки.

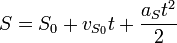
Инерциа́льнаясисте́ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся.

Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета.

Неинерциа́льнаясисте́ма отсчёта — система отсчёта, не являющаяся инерциальной. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.

При рассмотрении уравнений движения тела в неинерциальной системе отсчета необходимо учитывать дополнительные силы инерции. Законы Ньютона выполняются только в инерциальных системах отсчёта. Для того, чтобы найти уравнение движения в неинерциальной системе отсчёта, нужно знать законы преобразования сил и ускорений при переходе от инерциальной системы к любой неинерциальной.

Преобразова́нияГалиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой. Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время») и выполнение принципа относительности (принцип относительности Галилея (см. ниже)).

Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.

Если ИСО S движется относительно ИСО S' с постоянной скоростью 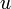вдоль оси 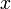, а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:

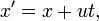
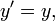
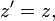
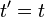
или, используя векторные обозначения,

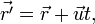
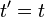
(последняя формула остается верной для любого направления осей координат).

Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).

Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:

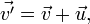
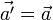
3)Угол поворота, угловые скорость и ускорение. Уравнение вращательного движения. Полное ускорение, центростремительное, тангенсальное. Связь вращательных их линейных величин.

Угол поворота - это физическая величина, характеризующая поворот тела, или поворот луча, исходящего из центра вращения тела, относительно другого луча, считающегося неподвижным.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

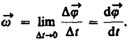
Линейная скорость точки

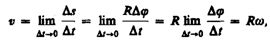
Если ( 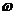= const, то вращение равномерное и его можно характеризовать периодомвращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени Dt = T соответствует 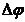=2p, то 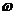=2p/T, откуда

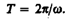
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

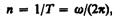
откуда

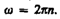
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

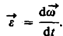
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор 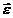сонаправлен вектору 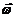(рис.8), при замедлен­ном — противонаправлен ему (рис.9).

Тангенциальная составляющая ускорения