Квадратура круга, удвоение куба, трисекция угла, теорема Ферма, проблема четырех красок.

Что такое закон природы?

Основные взаимосвязи между силами в природе описываются с помощью физических законов и принципов. К ним относятся:

v Принцип общей относительности (все законы физики должны быть одинаковы в любых системах отсчета)

v Принцип постоянства скорости света в вакууме в любых системах отсчета

v Принцип эквивалентности (никакими экспериментами невозможно отличить движение с ускорением от нахождения в однородном поле тяжести)

v К этому списку следует добавить фундаментальные соотношения квантовой механики, описывающие микромир. К наиболее важным относится:

v принцип неопределенности Гейзенберга, запрещающий одновременное точное измерение положения частицы в пространстве и ее импульса (количества движения)

v принцип Паули, запрещающий иметь в одном и том же месте пространства более двух частиц с полуцелым спином (т. н. фермионов электронов, нейтронов, нейтрино) с одним и тем же импульсом.

v Кроме того, для любой замкнутой системы должны выполняться первое и второе начало термодинамики (закон сохранения энергии и закон неубывания энтропии). По своей сути законы физики являются феноменологическими, то есть представляют собой обобщение опытных данных. В этом смысле космос часто по праву называют уникальной природной лабораторией, которой надо только умело пользоваться.

Попытки классификации взаимодействий привели к идее выделения минимального набора фундаментальных взаимодействий, при помощи которых можно объяснить все наблюдаемые явления. По мере развития естествознания этот набор менялся. В ходе экспериментальных исследований периодически обнаруживались новые явления природы, не укладывающиеся в принятый фундаментальный набор, что приводило к его расширению (например, открытие структуры ядра потребовало введения ядерных сил).

Теоретическое осмысление, стремящееся к единому, экономному описанию наблюдаемого многообразия, неоднократно приводило к «великим объединениям» внешне совершенно несхожих явлений природы. Так Ньютон понял, что падение яблока и движение планет вокруг Солнца являются результатами проявления гравитационных взаимодействий, Эйнштейн установил единую природу электрических и магнитных взаимодействий, Бутлеров опроверг утверждения о различной природе органических и неорганических веществ. В настоящее время принят набор из четырех типов фундаментальных взаимодействий: гравитационные, электромагнитные, сильное и слабое ядерные. Все остальные, известные на сегодняшний день, могут быть сведены к суперпозиции перечисленных.

Гравитационные взаимодействия обусловлены наличием у тел массы и являются самыми слабыми из фундаментального набора. Они доминируют на расстояниях космических масштабов (в мега-мире).

Электромагнитные взаимодействия обусловлены специфическим свойством ряда элементарных частиц, называемым электрическим зарядом. Играют доминирующую роль в макромире и микромире вплоть на расстояниях, превосходящих характерные размеры атомных ядер.

Ядерные взаимодействия играют доминирующую роль в ядерных процессах и проявляются лишь на расстояниях, сравнимых с размером ядра, где классическое описание заведомо неприменимо.

Наблюдения астрономических явлений привело человечество к ряду важнейших открытий. Самый известный и важный пример—закон всемирного тяготения. Этот закон был сформулирован И. Ньютоном на основе законов планетных движений, выведенных И. Кеплером в начале XVII в. Закон всемирного тяготения Ньютона используется до настоящего времени для изучения движения естественных и искусственных космических тел в Солнечной системе, так как релятивистские поправки к движению тела со скоростью в десятки км/с, очевидно, малы.

2. Причина и следствие.

Закон отрицания указывает направление развития является выражением поступательного прогрессивного движение осуществляемого по спирали, каждый следующий виток которой как бы повторяет предыдущий, но на более высокой основе. Все формы развития в своей основе содержат механизм возникновения и уничтожения всего существующего в результате действия определенных причин. Причинность есть связь, которая всегда вызывает появление нового качества. Причинность имеет всеобщий характер. Это значит, что у любого явления или события есть своя причина, беспричинных явлений не бывает. Причиной называют взаимодействие между телами или элементами одного и того же тела, вызывающее определенные изменения во взаимодействующих телах или элементах. Причина генетически связана со следствием, производит следствие. Следствие - это изменения, появляющиеся во взаимодействующих телах или элементах в результате их взаимодействия. Причинно-следственная связь является необходимой, т.е. определенная причина при наличии соответствующих условий вызывает одно и то же следствие. Итак, причина может вызывать соответствующее следствие лишь при наличии определенных условий. От характера условий зависят способ действия данной причины и природа следствия. Причину необходимо отличить от повода. Повод сам по себе не рождает следствие. Он является лишь внешним толчком, который способствует проявлению причины. Так, общепризнанным историческим фактом считается, что убийство австрийского эрцгерцога в Сараево привело в действие причины первой мировой войны. Причина и следствие находятся в диалектическом взаимодействии. Они постоянно меняются местами. Причина сама есть следствие какого-либо явления, а вызванное ею к жизни следствие становится причиной других явлений. Но этим не ограничивается диалектика причины и следствия. Причина играет определяющую роль по отношению к следствию. Однако в реальных процессах следствие не является пассивным и в свою очередь оказывает воздействие на свою причину.
Категории "причина" и "следствие" имеют большое значение для познания и практической деятельности. Физика, биология и другие науки добились значительных результатов, вскрывая механизм причинности в изучаемых областях действительности. Однако история философии знает мыслителей, которые ставили под сомнение возможность обнаружения причин. Например, Д. Юм утверждал, что опыт по части причинности свидетельствует лишь о связи во времени. Мы только наблюдаем, что во времени, следствие появляется за причиной. И это лишь психологическая привычка ума создает иллюзию логически необходимой связи между причиной и следствием, из которой никак нельзя делать вывод о том, что после этого значит поэтому. Согласно Юму, идея причинности имеет исключительно субъективное значение. Субъективная причинность существует в виде порождения идей чувственными впечатлениями. Из привычки видеть те или иные явления повторяющимися у людей возникает уверенность в наличии закономерностей. Всеобщий и объективный характер причинности утверждается детерминизмом. Он позволял на основе знания скорости и положения объекта в одно время вычислить скорость и его положение в другое время. Такой детерминизм применим при некоторых инженерных расчетах машин, мостов и других технических сооружений. Однако современная наука установила, что механическая причинность, действующая в мире макротел, не может быть реализована в микромиру, в объяснении психических и социальных явлений. Например, природа микрочастицы не позволяет в одно и то же время точно определить ее положение и скорость и исключает возможность на основании знания состояния объекта в настоящее время однозначно предсказать его поведение в будущем. Чем точнее установлено место микрочастицы, тем неопределеннее становится ее скорость и импульс. И, наоборот, чем точнее определена скорость, тем более неопределеннее становится ее положение. В итоге у некоторых философов и физиков возникла тенденция к абсолютизации этой неопределенности, и был сделан вывод о неприменимости принципа причинности к микромиру. Поэтому основные законы квантовой теории пытались объяснить в духе индетерминизма. Проблема неопределенности явно обнаруживается при рассмотрении эволюции хаотического движения. Однако синергетика утверждает, что детерминизм здесь вовсе не исключен, ибо в движении от хаоса к порядку в самом хаотическом движении существует конечный набор параметров, детерминирующих движение к порядку.
Развитие квантовой механики, выводы синергетики позволили иначе интерпретировать принцип детерминизма. Выяснилось, что сущность детерминизма заключается не в возможности однозначно предсказывать поведение объекта в будущем на основе знания его координат и импульса в настоящем, а в признании объективной закономерной взаимосвязи и взаимообусловленности вещей, явлений и процессов реального мира. Таким образом, противоположность детерминизма и индетерминизма снимается в диалектическом принципе всеобщей связи, который допускает связь, несводимую к силовому взаимодействию. С категориями "причина" и "следствие" генетически связаны категории "необходимость" и "случайность", которые представляют собой непосредственно следующую за причинностью ступень углубления человеческого познания в мир явлений.

3. Закон Архимеда. Закон всемирного тяготения.

«Эврика!» («Нашел!») — именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Архимед открыл принцип плавучести. Твердое тело погруженное в жидкость/газ, подвержено действию выталкивающей силы, равной весу жидкости, вытесненной телом. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело останется наплаву; в противном случае оно пойдет ко дну. Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено. Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории. В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, — и корабль плывет.

Закон всемирного тяготения

Исаак Ньютон выдвинул предположение, что между любыми телами в природе существуют силы взаимного притяжения. Эти силы называют силами гравитации, или силами всемирного тяготения. Сила всемирного тяготения проявляется в Космосе, Солнечной системе и на Земле. Ньютон обобщил законы движения небесных тел и выяснил,
что сила F равна: 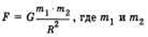- массы взаимодействующих тел, R — расстояние между ними, G — коэффициент пропорциональности, который называется гравитационной постоянной. Численное значение гравитационной постоянной опытным путем определил Кавендиш, измеряя силу взаимодействия между свинцовыми шарами. В результате закон всемирного тяготения звучит так: между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки.

Физический смысл гравитационной постоянной вытекает из закона всемирного тяготения. Если m1 = m2 = 1 кг, R = 1 м, то G = F, т. е. гравитационная постоянная равна силе, с которой притягиваются два тела по 1 кг на расстоянии 1 м. Численное значение: 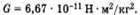Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах (или если хотя бы масса одного из тел велика). Закон же всемирного тяготения выполняется только для материальных точек и шаров (в этом случае за расстояние принимается расстояние между центрами шаров).
Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свободного падения. В соответствии со вторым законом Ньютона g = Ft*m следовательно, Ft = mg. Сила тяжести всегда направлена к центру Земли. В зависимости от высоты h над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с2.
В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете. Вес тела обозначается Р. Единица веса — Н. Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры.
Когда тело вместе с опорой не движется, сила реакции опоры, а следовательно, и вес тела равен силе тяжести.
Р = N = mg.
При движении вертикально вверх с ускорением вес тела увеличивается и находится по формуле Р = m(g + a).
Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают на себе космонавты как при взлете космической ракеты, так и при торможении корабля при входе в плотные слои атмосферы. Испытывают перегрузки и летчики при выполнении фигур высшего пилотажа, и водители автомобилей при резком торможении.
Если тело движется вниз по вертикали, то с помощью аналогичных рассуждений получаем 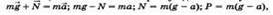т. е. вес при движении по вертикали с ускорением будет меньше силы тяжести.
Если тело свободно падает, то в этом случае P = (g- g)m = 0.
Состояние тела, в котором его вес равен нулю, называют невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением, поэтому в корабле наблюдается состояние невесомости.

Удвоение куба

В этой задаче требуетсяпостроить циркулем и линейкой куб вдвое большего объёма, чем заданный.
Ребро искомого куба равно a·2^1/3, где а — ребро исходного куба. Если принять, что а= 1, то искомое ребро х есть корень уравнения X³ - 2 = 0. У данного уравнения нет рациональных, а
значит, и квадратично-иррациональных корней. Следовательно, удвоение куба нельзя
осуществить циркулем и линейкой. Примерно такое расуждение было применено в начале XIX в., когда был подготовлен необходимый для этого алгебраический аппарат. Считают, что задача об удвоении куба появилась во времена пифагорейцев, около 540 г. до н. э. Возможно, она возникла из задачи об удвоении квадрата, которую легко решить, опираясь на теорему Пифагора, — надо построить квадрат на диагонали данного квадрата. Согласно легенде, жители Афин, на которых боги ниспослали эпидемию чумы, отправили делегацию к оракулу на остров Делос за советом, как задобрить богов и избавиться от морового поветрия. Ответ был таков: «Удвойте жертвенник храма Аполлона, и чума прекратится». Жертвенник имел кубическую форму. Афиняне решили, что задание простое, и построили новый жертвенник, с вдвое большим ребром. Однако чума только усилилась, Вторично обратились к оракулу и получили ответ: «Получше изучайте геометрию». История умалчивает о том, как удалось умилостивить богов, но чума в конце концов покинула город. А задачу об удвоении куба стали называть делосской задачей. Известна и другая легенда. Греческий комментатор VI в. до н. э. сообщает о письме, предположительно написанном царю Птолемею I. В нём говорится, что царь Минос построил на могиле сына надгробие кубической формы, но остался недоволен размерами памятника и приказал удвоить его, увеличив вдвое ребро куба. Комментатор указывает на ошибку царя Миноса (площадь поверхности памятника в результате увеличилась в четыре, а объём — в восемь раз) и рассказывает, что тогда геометры попытались решить эту задачу. Но так и не сумев с ней справиться с помощью циркуля и линейки, греки попробовали применить другие инструменты, механизмы и даже специальные кривые. Гиппократ Хиосский, знаменитый геометр V в. до н. э., свёл удвоение куба к построению «двух средних пропорциональных» х и у для данных отрезков а и b, т.е. к. решению уравнений а : х = х : у = у : b (при b = 2а получаем х = а ·2^1/3). Эту идею удалось реализовать Платону около 340 г. до н. э. с помощью нетрадиционных чертёжных инструментов — двух прямых углов. Свои решения дали также крупнейшие древнегреческие математики Евдокс, Эратосфен, Аполлоний, Герон, Папп, и др. Никомед из Александрии (2 в. до н. э.) использовал для решения этой задачи особую кривую — конхоиду (слово «конхоидео в переводе с греческого означает «подобная раковине мидии»). Диоклес придумал для решения этой задачи замечательную кривую - циссоиду (от греч.«киссоидес» - «плющевидный»). Менехм примерно в 350 г. до н.э. решал задачу об удвоении куба, используя конические сечения — кривые, по которым плоскости пересекают конус.

Трисекция угла

Несложно разделить любой угол с помощью циркуля и линейки на две, а некоторые углы - и на три равные части. Последняя операция называется трисекцией угла. Например, мы можем построить треть прямого угла, поделив пополам угол правильного треугольника, а проведя биссектрису в образовавшемся угле в 30°, получим угол величиной 15° — треть угла в 45°. Есть и другие углы, для которых трисекция выполнима. Наверное, подобные построения и вселили надежду открыть способ трисекции любого угла посредством циркуля и линейки. Эту задачу пытались решить ещё в V в. до н. э. в Греции. Гиппий Элидский (около 420 г. до н, э.) для трисекции угла использовал кривую, впоследствии названную квадратрисой. Никомед с той же целью чертил свою конхоиду сполюсом О, основанием р и интервалом 2ОВ; она пересекает l в искомой точке Q.Французский математик П. Ванцель к 1837 г, первым строго доказал, что невозможно осуществить трисекцию циркулем и линейкой.
Пусть а = р/3. По известной формуле, cos р = 4cos³ а - 3cos а. Тогда для величины х =
=2 cos р получается уравнение х³ - 3х - к = О, где к =2cos р. Геометрическая задача трисекции данного угла с циркулем и линейкой разрешима тогда и только тогда, когда полученное алгебраическое уравнение разрешимо в квадратных радикалах. Возьмём, например, р = 60°. Тогда уравнение примет вид х³ - 3х - 1 = 0. Оно неразрешимо в квадратных радикалах, а потому и трисекция с помощью циркуля и линейки в данном случае невозможна. Тем более она невозможна в общем случае.
Интересно, что вообще для углов вида 360°/n с целым n трисекцию удаётся осуществить тогда и только тогда, когда n не делится на 3.

Теорема Ферма

Большой известностью во всём мире пользуется «Великая теорема Ферма» (она же – «Большая» или «Последняя»). Великой теоремой Ферма называется то заключение, которое было сделано им при чтении изданной Мезириаком «Арифметики» Диофанта. Это положение Ферма теперь формулируется как теорема в следующем виде: «Уравнение xn+ yn= znне может быть решено в рациональных числах относительно x, y и z при целых значениях показателя n, больших 2» (общеизвестно, что при n=2 такие числа существуют, например, 3, 4, 5 – числа, которые, если являются длинами сторон, образуют знаменитый треугольник Пифагора). Справедливость этой теоремы подтверждается для многих частных случаев (при этом ещё не найдено ни одного опровержения), однако до сих пор она не доказана в общем виде, хотя ей интересовались и её пытались доказать многие крупные математики (в «Истории теории чисел» Диксона прореферировано более трёхсот работ на эту тему). В 1907 году в городе Дармштадте в Германии умер математик Вольфскель, который завещал 100000 марок тому, кто даст полное доказательство теоремы. Но премия эта до сих пор никому не выдана за отсутствием настоящего доказательства Большой теоремы Ферма. Элементарного доказательства Великой теоремы Ферма нет ни для одного показателя n 4. Случай, когда n = 3, был доказан Эйлером ещё в 1768 году. И тот потребовал ещё много лет, чтобы теория, которой необоснованно пользовался Эйлер при своём доказательстве, была доказана Гауссом. Доказательство теоремы Ферма для случая, когда n = 5, предложили в 1825 году почти одновременно Лежен Дирихле и Лежандр. Своё доказательство Дирихле опубликовал в 1828 году, но оно было очень сложным, и в 1912 году его упростил Племель. Для следующего простого показателя n = 7 теорема Ферма была доказана лишь в 1839 году Ламе. Доказательство Ламе было почти сразу же усовершенствовано Лебегом. В 1847 году Ламе объявил, что ему удалось найти доказательство теоремы Ферма для всех простых показателей n 3. Метод Ламе представлял собой весьма далёкое развитие идей Эйлера и основывался на арифметических свойствах чисел. Однако сразу же Лиувилль обнаружил в рассуждениях Ламе серьёзный пробел, чем опровергнул это доказательство. Ламе был вынужден признать свою ошибку. На ЭВМ, пользуясь идеями Куммера и Вандивера доказали справедливость теоремы Ферма для всех простых показателей n< 100000.

Проблема четырёх красок

Исторически понятие хроматического числа возникло с проблемой четырех красок. Проблема возникла в математике в середине 19 века. Первоначально вопрос формулировался так: сколько нужно красок для раскраски любой географической карты, при которой соседние страны раскрашены в разные цвета? Под географической картой понимается разбиение плоскости на конечное число связных областей, стран, границы которых состоят из замкнутых непрерывных линий без самопересечений, а соседними являются страны, имеющие общую границу ненулевой длины. Довольно очевидно, что четырех красок недостаточно. и вопрос формулировался обычно в более конкретном виде: достаточно ли четырех красок для раскраски любой географической карты? Это и есть проблема четырех красок. Положительный ответ на вопрос называется гипотезой четырех красок. Проблема раскраски географических карт сводится к проблеме (правильной) раскраски плоских графов. Проиллюстрируем это сведение картой, изображенной на рис.5.9.

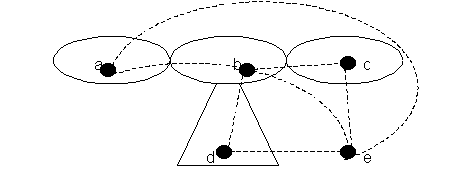
Рис.5.9

На рисунке изображена карта, имеющая пять стран (внешняя область - тоже страны). Внутри каждой страны зафиксируем точку, точки соединим ребром, если страны имеют общую границу. (На рис.5.9 ребра проведены пунктирными линиями). Ребра при этом можно провести так, чтобы они не пересекались, т.е. чтобы полученный граф был плоским. Ясно, что раскраска карты определяет правильную раскраску графа и обратно. Проблему четырех красок можно теперь сформулировать так: достаточно ли четырех красок для правильной раскраски плоского графа? Эта проблема вызвала большой интерес в математике. Есть свидетельства, что ей занимались известные математики Мебиус и де Морган. В 1880 году А. Компе опубликовал положительное решение проблемы четырех красок. Однако в 1890 году Р. Хивуд обнаружил ошибку в этом доказательстве. Одновременно он показал, что пяти красок достаточно для раскраски любого плоского графа (см. §4). После этого появлялось довольно много «доказательств» гипотезы четырех красок и «контрпримеров» к ней, в которых обнаруживались ошибки. В 1969 году Х. Хели свел проблему четырех красок к исследованию множества С так называемых конфигураций. Множество с является конечным. Но довольно большим (порядка нескольких тысяч). Несколькими годами позже, в 1976 году математикам К. Аппелю и В. Хейкену удалось показать. Что все конфигурации из множества С можно правильно раскрасить в четыре цвета. В возникающем при этом переборе существенно использовался компьютер. Такое решение проблемы четырех красок долгое время не признавалось многими математиками. Поскольку его сложно повторить. Однако сейчас практически общепризнано, что К. Аппелем и В. Хейкеном доказана гипотеза четырех красок.

Часть 2. Законы сохранения.

Ограничимся только физикой, там они наиболее жесткие.

Некоторые величины в изолированных системах, сохраняются, тюею система меняется, но некотор. особо важные величины сохраняются.

Закон сохранения импульса имомента импульса(вращательный момент).

Закон сохранения энергии(самый важный закон для физики) (XIXв.)так долго не могли открыть этот закрн так не знали свех видов (взаимодействия энергии)

Сейчас уже хорошо описаны все виды взаимодействий.доказано,что во всех энергия сохраняется!

Закон сохранения энергии

Закон сохранения энергии - следствие симметрии природы относительно сдвигов во времени. Допустим, что неравномерность хода времени проявилась в том, что, начиная с некоторого момента времени, стала периодически изменяться постоянная всемирного тяготения. Тогда легко построить машину, которая будет получать энергию ни из чего - "вечный двигатель". Для этого нужно поднимать грузы в период слабого тяготения и превращать приобретенную ими энергию в кинетическую, сбрасывая грузы в период увеличения тяготения. Из сказанного следует, что однородность хода времени можно проверить по тому, насколько точно выполняется закон сохранения энергии.

Связь законов сохранения с симметрией системы. Ответ на естественный вопрос о том, почему справедливы законы сохранения в физике был найден сравнительно недавно. Оказалось, что законы сохранения возникают в системах при наличии у них определенных элементов симметрии. (Элементом симметрии системы называется любое преобразование, переводящие систему в себя, т.е. не изменяющее ее. Например элементом симметрии квадрата является поворот на прямой угол вокруг оси, проходящей через его центр - “ось вращения четвертого порядка”).

Глобальные законы сохранения связаны с существованием таких преобразований, которые оставляют неизменными любую систему. К ним относятся:

Закон сохранения энергии, являющийся следствием симметрии относительно сдвига вовремени (однородности времени).

Закон сохранения импульса, являющийся следствием симметрии относительно параллельного переноса в пространстве (однородности пространства).

Закон сохранения момента импульса, являющийся следствием симметрии относительно поворотов в пространстве (изотропности пространства).

Закон сохранения заряда, являющийся следствием симметрии относительно замены описывающих систему комплексных параметров на их комплексно сопряженные значения.

Закон сохранения четности, являющийся следствием симметрии относительно операции инверсии (“отражения в зеркале”, меняющего “право” на “лево”).

Закон сохранения энтропии, являющийся следствием симметрии относительно обращения времени.

Кратко рассмотрим законы сохранения механических величин.

Закон сохранения импульса. Каждой материальной точке с массой m, движущейся со скоростью V,приписывается векторная характеристика - импульс, определяемый как произведение Массы на скорость:

Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил:

В случае системы материальных точек (совокупностью которых можно считать любое реальное тело) полный импульс определяется как векторная сумма всех импульсов

Скорость изменения полного импульса определяется суммой внешних сил, действующих на систему (т.е. только сил, описывающих взаимодействие элементов системы с не принадлежащими ей объектами):

Системы, на которые не действуют внешние силы, называются замкнутыми. В них полный импульс не изменяется во времени. Это свойство находит большое практическое применение, поскольку лежит в основе принципа реактивного движения (рис. .5_1)..

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях, когда Ньютоновская механика неприменима (релятивистская физика, квантовая механика). Как отмечалось, он может быть получен как следствие интуитивно-верного утверждения о том, что свойства нашего мира не изменятся, если все его объекты (или начало отсчета!) переместить на некоторый вектор L.В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.

Нётер теорема, фундаментальная теорема физики, устанавливающая связь между свойствами симметрии физической системы и законами сохранения. Сформулирована Э. Нётер в 1918. Н. т. утверждает, что для физической системы, уравнения движения которой имеют форму системы дифференциальных уравнений и могут быть получены из вариационного принципа механики,

(Вариационные принципы механики. Принципами механики называются исходные положения, отражающие столь общие закономерности механических явлений, что из них как следствия можно получить все уравнения, определяющие движение механической системы (или условия её равновесия). В ходе развития механики был установлен ряд таких принципов, каждый из которых может быть положен в основу механики, что объясняется многообразием свойств и закономерностей механических явлений. Эти принципы подразделяют на невариационные и вариационные.)

каждому непрерывно зависящему от одного параметра преобразованию, оставляющему инвариантным вариационный функционал, соответствует закон сохранения. В механике частиц или полей вариационным функционалом служит действие S; из условия обращения в нуль вариации действия S = 0 (наименьшего действия принцип) получаются уравнения движения системы. Каждому преобразованию, при котором действие не меняется, соответствует дифференциальный закон сохранения. Интегрирование уравнения, выражающего такой закон, приводит к интегральному закону сохранения.

Н. т. даёт наиболее простой и универсальный метод получения законов сохранения в классической и квантовой механике, теории поля и т. д.

Непрерывными преобразованиями в пространстве-времени, оставляющими инвариантным действие (а следовательно, и уравнения движения), являются: сдвиг во времени (что выражает физическое свойство равноправия всех моментов времени — однородность времени), сдвиг в пространстве (свойство равноправия всех точек пространства — однородность пространства), трёхмерное пространственное вращение (свойство равноправия всех направлений в пространстве — изотропия пространства), четырёхмерные вращения в пространстве-времени, в частности Лоренца преобразования, выражающие принцип относительности. Согласно К. т., из инвариантности относительно сдвига во времени следует закон сохранения энергии; относительно пространственных сдвигов — закон сохранения импульса; относительно пространственного вращения — закон сохранения момента количества движения; относительно преобразований Лоренца — закон сохранения лоренцова момента, или обобщённый закон движения центра масс (центр масс релятивистской системы движется равномерно и прямолинейно).

Закон сохранения энергии

Закон сохранения энергии - следствие симметрии природы относительно сдвигов во времени. Допустим, что неравномерность хода времени проявилась в том, что, начиная с некоторого момента времени, стала периодически изменяться постоянная всемирного тяготения. Тогда легко построить машину, которая будет получать энергию ни из чего - "вечный двигатель". Для этого нужно поднимать грузы в период слабого тяготения и превращать приобретенную ими энергию в кинетическую, сбрасывая грузы в период увеличения тяготения. Из сказанного следует, что однородность хода времени можно проверить по тому, насколько точно выполняется закон сохранения энергии.

Закон сохранения энергии, являющийся следствием симметрии относительно сдвига вовремени (однородности времени).

К непрерывным преобразованиям относятся следующие.

1) Перенос(сдвиг) системы как целого в пространстве. Симметрия физических законов относительно сдвигов в пространстве означает эквивалентность всех точек пространства, то есть отсутствие в пространстве каких-либо выделенных точек (однородность пространства).

2) Изменение начала отсчета времени (сдвиг во времени); симметрия относительно этого преобразования означает эквивалентность всех моментов времени (однородность времени), благодаря которой физические законы не меняются со временем.

3) Поворот системы как целого в пространстве; симметрия физических законов относительно этого преобразования означает эквивалентность всех направлений в пространстве (изотропию пространства).

4) Переход к системе отсчета, движущейся относительно данной системы с постоянной (по направлению и величине) скоростью. Симметрия относительно этого преобразования означает, в частности, эквивалентность всех инерциальных систем отсчета.

Вечный двигатель.

До того, как был открыт закон сохранения энергии, в течение столетий упорно делались попытки создать такую машину, кот