Напряженность и потенциал электростатического поля
Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измеренияпотенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда (для любой системы единиц; подробнее о единицах измерения — см. ниже).
Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.
Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:
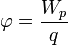
Напряжённость электростатического поля 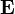 и потенциал
и потенциал 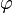 связаны соотношением[1]
связаны соотношением[1]
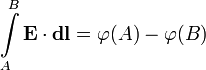
или обратно[2]:
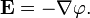
Здесь  — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.
— оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.
Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля 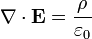 , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона. В единицах системы СИ:
, легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона. В единицах системы СИ:
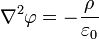
где 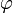 — электростатический потенциал (в вольтах),
— электростатический потенциал (в вольтах), 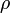 — объёмная плотность заряда (в кулонах на кубический метр), а
— объёмная плотность заряда (в кулонах на кубический метр), а 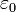 — диэлектрическая проницаемость вакуума (в фарадах на метр).
— диэлектрическая проницаемость вакуума (в фарадах на метр).
4)Графическое изображение электрического поля
Электрическое поле изображается графически с помощью так называемых силовых линий
Фарадей изображал электрическое поле наглядно, графически, с помощью силовых линий – касательные к которым направлены как сила, по направлению совпадают с напряженностью.Поле точечного заряда.Силовые линии условно начинают на положительных зарядах и заканчивают на отрицательных. Напряженность поля можно связать с густотой силовых линий, они гуще, где больше напряженность, и не пересекаются, иначе бы она не имела определенного направления.
Поля точечных положительных и отрицательных зарядов, одного и разного знака показаны на рис.8.8.
Систему двух противоположных зарядов (-q+q)на расстоянииlназывают электрическим диполем и характеризуютэлектрическим дипольным моментомd=ql(направленным по оси -+).
Эти моменты могут характеризовать поле атомов и молекул (11. ), определяют полярность, поляризацию и диэлектрическую проницаемость веществ, изменяющие силы (ε).
Кулоновские силы и напряженности электрического поля подчиняются принципу суперпозиции, равны геометрической сумме составляющих, созданных каждым зарядом в отдельности:Е=Е1+Е2+…+Еn(как будто другие заряды не влияют на поле каждого).
5)Принцип суперпозиции
При́нципсуперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
· результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:
· Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.
· Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нетмногочастичных взаимодействий.
· Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.
Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.
6)Связь напряженности и потенциала
Разные пробные заряды q',q'',… будут обладать в одной и той же точке поля разными энергиями W', W'' и так далее. Однако отношение 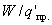 будет для всех зарядов одним и тем же.Поэтому можно вести скалярную величину, являющуюся энергетической характеристикой собственно поля – потенциал:
будет для всех зарядов одним и тем же.Поэтому можно вести скалярную величину, являющуюся энергетической характеристикой собственно поля – потенциал:
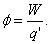 | (3.3.1) |
Из этого выражения следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Подставив в (3.3.1.) значение потенциальной энергии (3.2.4), получим для потенциала точечного заряда следующее выражение:
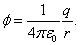 | (3.3.2) |
Потенциал, как и потенциальная энергия, определяют с точностью до постоянной интегрирования. Поскольку физический смысл имеет не потенциал, а разность потенциалов, поэтому договорились считать, что потенциал точки, удаленной в бесконечность, равен нулю. Когда говорят «потенциал такой-то точки» – имеют в виду разность потенциалов между этой точкой и точкой, удаленной в бесконечность. Другое определение потенциала:
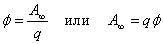 ,
,
т.е. потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность (илинаоборот – такую же работу нужно совершить, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля). При этом 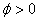 , если q > 0.
, если q > 0.
Если поле создается системой зарядов, то, используя принцип суперпозиции, получаем:
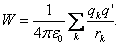 | (3.3.3) |
Тогда и для потенциала 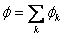 или<
или<
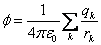 , , | (3.3.4) |
т.е. потенциал поля, создаваемый системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности<. А вот напряженностискладываются при наложении полей – векторно. По этой причине потенциалы полей считать проще, чем напряженности.
Вернемся к работе сил электростатического поля над зарядом q. Выразим работу через разность потенциалов между начальной и конечной точками:
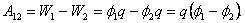 | (3.3.5) |
Таким образом, работа над зарядом q равна произведению заряда на убыль потенциала. То есть
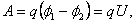
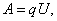 | (3.3.6) |
где U – напряжение.
(Между прочим, хорошая аналогия с гравитационным полем:
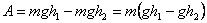 ,
,
здесь gh – имеет смысл потенциала, а m – заряда гравитационного поля).
Итак, потенциал – скалярная величина, поэтому пользоваться и вычислять φ проще, чем 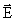 . Приборы для измерения разности потенциалов широко распространены.
. Приборы для измерения разности потенциалов широко распространены.
Формулу 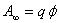 можно использовать для установления единиц потенциала: за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного положительного заряда необходимо совершить работу равную единице.
можно использовать для установления единиц потенциала: за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного положительного заряда необходимо совершить работу равную единице.
В СИ – единица потенциала 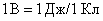 .
.
7)Циркуляция вектора напряженности электростатического поля - ?
Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории (рис. 132) перемещается другой точечный заряд Q0, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна
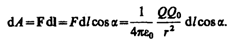
Так как d/cosa=dr, то
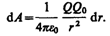
Работа при перемещении заряда Q0 из точки 1 в точку 2
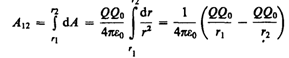
(83.1)
не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными.
8)Поток вектора напряженности электрического поля
Как и для любого векторного поля важно рассмотреть свойства потока электрического поля. Поток электрического поля определяется традиционно.
Выделим малую площадку площадью ΔS, ориентация которой задается единичным вектором нормали n⃗ (рис. 157).
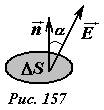
В пределах малой площадки электрическое поле можно считать однородным [1], тогда поток вектора напряженности ΔФE определяется как произведение площади площадки на нормальную составляющую вектора напряженности
ΔΦE=EcosαΔS=(E⃗ ⋅n⃗ )ΔS=EnΔS . (1)
где (E⃗ ⋅n⃗ )=Ecosα — скалярное произведение векторов E⃗ и n⃗ ; En — нормальная к площадке компонента вектора напряженности.
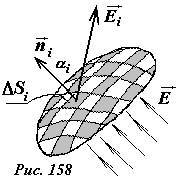
В произвольном электростатическом поле поток вектора напряженности через произвольную поверхность, определяется следующим образом (рис. 158):
- поверхность разбивается на малые площадки ΔS (которые можно считать плоскими);
- определяется вектор напряженности E⃗ на этой площадке (который в пределах площадки можно считать постоянным);
- вычисляется сумма потоков через все площадки, на которые разбита поверхность
Φ=ΔΦ1+ΔΦ2+ΔΦ3+…=∑iΔΦi=∑iEicosαiΔSi .
Эта сумма называется потоком вектора напряженности электриче-ского поля через заданную поверхность. Трудно найти явный физический смысл этой величины, но как мы указывали, поток векторного поля является полезной вспомогательной математической величиной.
Рассмотрим электрическое поле точечного заряда Q (рис. 159). Это поле обладает сферической симметрией — модуль вектора напряженности зависит только от расстояния для заряда, в любой точке вектор напряженности направлен радиально, вдоль прямой, соединяющей заряд с точкой наблюдения.
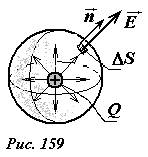
Окружим заряд сферой, произвольного радиуса R, центр которой совпадает с точечным зарядом. Во всех точках поверхности сферы вектор напряженности электрического поля направлен вдоль нормали к поверхности сферы (поэтому угол между ними равен нулю), его модуль постоянен и по закону Ш. Кулона равен
E=Q4πε0R2 .
Выделим на поверхности сферы малую площадку площадью ΔSi, поток вектора напряженности через эту площадку равен
ΔΦi=Q4πε0R2ΔSi .
Так как модуль вектора напряженности во всех точках сферы одинаков, суммирование потоков через поверхность сферы, сводится к суммированию площадей участков, на которые разбивается сфера. Вычислим поток вектора напряженности
ΦE=∑iQ4πε0R2ΔSi=Q4πε0R2∑iΔSi=Q4πε0R2⋅4πR2=Qε0 , (2)
здесь ∑iΔSi=4πR2 — площадь поверхности сферы. Обратите внимание, что этот поток не зависит от радиуса сферы. Итак, поток вектора напряженности электрического поля точечного заряда через поверхность сферы равен отношению заряда к электрической постоянной.
9)Теорема Гаусса в интегральной форме и ее применение для расчета электрических полей
Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.
Аналогичная теорема, также входящая в число уравнений Максвелла, существует и для магнитного поля (см. ниже).
Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния[1] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).
В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.
Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.
10)Вычисление разности потенциалов по напряженности поля
| тело | разность потенциалов |
Бесконечная заряженная плоскость 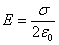 | 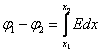 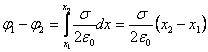 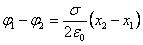 |
Две параллельных бесконечных плоскости 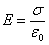 | 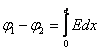 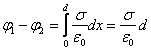 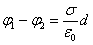 |
Сферическая поверхность радиуса R 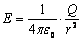 (r (r 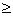 R) R) 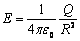 ( ( 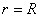 ) ) 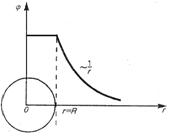 | 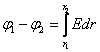 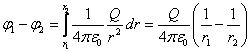 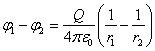 Если Если 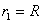 и и 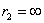 , то потенциал вне сферы: , то потенциал вне сферы: 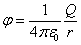 Внутри сферы потенциал одинаков и равен: Внутри сферы потенциал одинаков и равен: 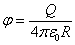 |
Объемно заряженный шар 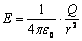 (r (r 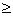 R) R) 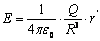 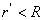 | Разность потенциала между точками за пределами шара определяется так же как и для сферы: 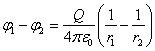 Внутри шара разность потенциалов равна: Внутри шара разность потенциалов равна: 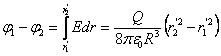 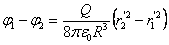 |
Или
Напряжённость, силовая характеристика поля, и разность потенциалов, его энергетическая характеристика, связаны однозначно. Вычислим работу поля при малом перемещении заряда двумя способами:
A=qEΔlcosα=qElΔl;где α - угол между векторами напряжённости и перемещения, El- проекция напряжённости на перемещение.
A=-qΔφ.
Приравнивая, получаем:
ElΔl=-Δφ=U.
Зная напряжённость в каждой точке, можно вычислить разность потенциалов между любыми точками. Зная разность потенциалов между любыми точками, можно вычислить проекцию напряжённости на направление между ними.
El=-Δφ/Δl=U/Δl.
Отсюда следует,что напряжённость направлена в сторону убывания потенциала. Эта формула позволяет также определить вторую единицу напряжённости - вольт на метр (В/м). 1В/м=1Н/Кл.
дополнительно(При перемещении заряда под прямым углом к линиям напряжённости работа поля равна нулю, так как сила перпендикулярна перемещению. Следовательно, все точки поверхности, перпендикулярной в каждой точке линиям напряжённости имеют одинаковый потенциал. Такие поверхности называют эквипотенциальными. Эквипотенциальные поверхности, как и силовые линии, позволяют наглядно представить электрическое поле.
Эквипотенциальные поверхности однородного поля - параллельные плоскости, точечного заряда - концентрические сферы. Поверхность любого проводника является эквипотенциальной, так как напряжённость направлена перпендикулярно ей. Потенциал всех точек внутри проводника одинаков, потому что, раз напряжённость поля в проводнике равна нулю, то равна нулю и разность потенциалов.
Разность потенциалов и напряжённость являются количественными характеристиками поля. Напряжённость более наглядна и указывает направление силы, действующей на заряд. Но разность потенциалов тоже имеет свои преимущества. Разность потенциалов легче измерить, чем напряжённость. Потенциал - скаляр, поэтому задаётся одним числом, а напряжённость - вектор, поэтому задаётся тремя числами - проекциями на оси кооординат. Многие процессы и величины (например, сила тока) определяются не силой, действующей со стороны поля, а его энергией и работой, то есть разностью потенциалов.)
11)Электрическое поле диполя
Электрическое поле диполя
Для фиксированных угловых координат (то есть на луче, идущем из центра электрического диполя на бесконечность) напряжённость статического[прим 4] электрического поля диполя или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент,[прим 5] на больших расстояниях r асимптотически приближается к виду r−3, электрический потенциал — к r−2. Таким образом, статическое поле диполя убывает на больших расстояниях быстрее, чем поле простого заряда (но медленнее, чем поле любого более старшегомультиполя).
Напряжённость электрического поля и электрический потенциал неподвижного или медленно движущегося диполя (или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент) с электрическим дипольным моментом 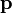 на больших расстояниях в главном приближении выражается как:
на больших расстояниях в главном приближении выражается как:
в СГСЭ: 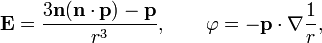
в СИ: 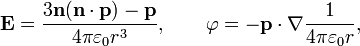
где 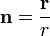 — единичный вектор из центра диполя в направлении точки измерения, а точкой обозначено скалярное произведение.
— единичный вектор из центра диполя в направлении точки измерения, а точкой обозначено скалярное произведение.
Достаточно просты выражения (в том же приближении, тождественно совпадающие с формулами, приведенными выше) для продольной (вдоль радус-вектора, проведенного от диполя в данную точку) и поперечной компонент напряженности электрического поля:
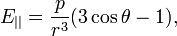
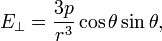
где 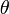 — угол между направлением вектора дипольного момента и радиус-вектором в точку наблюдения (формулы приведены в системе СГС; в СИ аналогичные формулы отличаются только множителем
— угол между направлением вектора дипольного момента и радиус-вектором в точку наблюдения (формулы приведены в системе СГС; в СИ аналогичные формулы отличаются только множителем 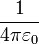 ). Третья компонента напряженности электрического поля — ортогональная плоскости, в которой лежат вектор дипольного момента и радиус-вектор, — всегда равна нулю.
). Третья компонента напряженности электрического поля — ортогональная плоскости, в которой лежат вектор дипольного момента и радиус-вектор, — всегда равна нулю.
12)Диполь во внешнем электрическом поле
Найдем момент сил, действующих на диполь в однородном электрическом поле. Пусть положения положительного и отрицательного зарядов относительно центра диполя характеризуются векторами r+и r-, соответственно. Тогда, в соответствии с определением момента сил, имеем.
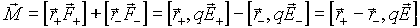
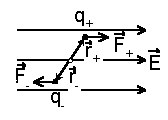 Рис. 3.4 Рис. 3.4 | Так как по определению 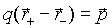 , то окончательно получим , то окончательно получим
|
Момент сил, очевидно, равен нулю, когда векторы pи Eколлинеарны, однако устойчивым положением является только такое положение, когда они еще и совпадают по направлению. В однородном поле, очевидно, F+ +F_= 0.
Если диполь находится в неоднородном внешнем электрическом поле, то равнодействующая сил, действующих на положительный и отрицательный заряды диполя оказывается не равной нулю:
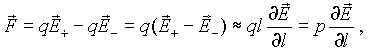 | (3.10) |
гдеE+ иE_ - напряженность поля в точках расположения положительного и отрицательного зарядов, соответственно, а разностьE+ -E_ есть приращение вектора Eна отрезке, равном длине диполя, взятом в направлении его оси. В выражение (3.10) входит так называемая производная вектора по направлению, которая в общем случае определяется довольно сложно. Рассмотрим простейший случай, когда неоднородное поле обладает симметрией относительно оси x. Пусть ось диполя также направлена вдоль оси x. Тогда сила будет иметь составляющую только вдоль осиx, равную
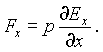
Если, например, поле убывает в направлении оси диполя, то производная в последнем выражении будет отрицательной, и диполь будет втягиваться в область более сильного поля.
Находясь во внешнем поле, диполь обладает некоторой энергией помимо энергии взаимодействия зарядов его составляющих.
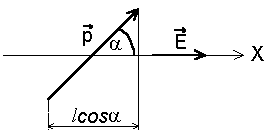 Рис. 3.5 Рис. 3.5 | Пусть диполь находится в однородном электрическом поле. Направим ось x вдоль вектора E. Поскольку 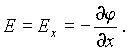 то потенциальная энергия диполя будет равна то потенциальная энергия диполя будет равна |
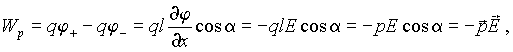
где a - угол между осью диполя и направлением поля.
13)Типы диэлектриков
Диэлектриками называются вещества, которые в обычных условиях практически не проводят электрический ток, их удельное сопротивление в 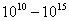 раз больше, чем у металлов. Согласно представлениям классической физики, в диэлектриках, в отличие от проводников, нет свободных носителей заряда, которые могли бы под действием электрического поля создавать ток проводимости.
раз больше, чем у металлов. Согласно представлениям классической физики, в диэлектриках, в отличие от проводников, нет свободных носителей заряда, которые могли бы под действием электрического поля создавать ток проводимости.
К диэлектрикам относятся все газы; некоторые жидкости (дистиллированная вода, масла, бензол); твердые тела (стекло, фарфор, слюда). Термины "диэлектрик" и "диэлектрическая постоянная" были введены в науку в 1837 г. M. Фарадеем.
Диэлектрики, как и любые вещества, состоят из атомов и молекул. В целом молекулы нейтральны, тем не менее, они взаимодействуют с электрическим полем. Например, в случае, когда симметрия молекулы отлична отсферической, ее можно представить в виде электрического диполя. Электрический дипольный момент молекулы  , где q - суммарный заряд ядер или электронов; l - вектор, представляющий собой плечо эквивалентного диполя.
, где q - суммарный заряд ядер или электронов; l - вектор, представляющий собой плечо эквивалентного диполя.
Молекулы, обладающие электрическим дипольным моментом, называют полярными. Полярным диэлектриком является вода; следующие вещества: CO; N2O; S2O; NH; HCl также имеют в своем составе полярные молекулы. В объеме вещества дипольные моменты молекул распределены по разным направлениям хаотическим образом, так что их сумма равна нулю 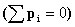 .
.
Молекулы, у которых положения эквивалентного положительного и эквивалентного отрицательного заряда совпадают и, следовательно, дипольный момент каждой молекулы равен нулю ( 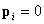 ), называют неполярными. Такие вещества, как
), называют неполярными. Такие вещества, как 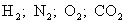 состоят из неполярных молекул.
состоят из неполярных молекул.
Если диэлектрик внести в электрическое поле, то это поле и сам диэлектрик претерпевают существенные изменения.
14). Поляризация диэлектриков
Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.
Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.
· Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков).
Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема.
Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает всегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры.
Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е1, направленное против внешнего поля с напряженностью Е0. Результирующая напряженность поля Е внутри диэлектрика Е=Е0-Е1.
15)Ориентационный и деформационный механизмы поляризации
Ориентационная (дипольная) поляризация возникает в полярных диэлектриках (рис. 2.3). На каждый из зарядов диполя, внесенного в однородное электрическое поле с напряженностью 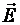 , будут действовать равные по модулю силы
, будут действовать равные по модулю силы 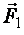 и
и 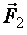 , направленные в противоположные стороны. Они создадут момент сил М, стремящийся повернуть молекулу-диполь так, чтобы его дипольный момент совпадал по направлению с вектором напряженности электрического поля. Вектор момента сил равен
, направленные в противоположные стороны. Они создадут момент сил М, стремящийся повернуть молекулу-диполь так, чтобы его дипольный момент совпадал по направлению с вектором напряженности электрического поля. Вектор момента сил равен 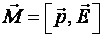 или по модулю
или по модулю 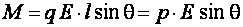 . Таким образом, каждая молекула-диполь будет испытывать ориентирующее действие поля.
. Таким образом, каждая молекула-диполь будет испытывать ориентирующее действие поля.
(?) Электронные оболочки и ядра упруго смещаются друг относительно друга, поэтому такой вид поляризации часто называют деформационной поляризацией. Поскольку ядра в 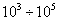 раз тяжелее электронов, то смещение испытывают в основном электроны, причем преимущественно валентные как более слабо связанные с ядром по сравнению с электронами более глубоких оболочек. Вследствие смещения электронных орбит поляризованная частица (атом или молекула) становится электрическим диполем с определенным наведенным (индуцированным) электрическим моментом, равным произведению заряда на величину смещения.
раз тяжелее электронов, то смещение испытывают в основном электроны, причем преимущественно валентные как более слабо связанные с ядром по сравнению с электронами более глубоких оболочек. Вследствие смещения электронных орбит поляризованная частица (атом или молекула) становится электрическим диполем с определенным наведенным (индуцированным) электрическим моментом, равным произведению заряда на величину смещения.
Такой механизм поляризации наименее инерционен, время ее установления составляет всего 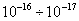 с. Это приводит к тому, что при электронной упругой поляризации в веществе успевает устанавливаться поляризованное состояние даже при сравнительно высоких частотах электромагнитного поля (оптические колебания видимого и инфракрасного спектров), что приводит к слабому поглощению такого излучения в веществе.
с. Это приводит к тому, что при электронной упругой поляризации в веществе успевает устанавливаться поляризованное состояние даже при сравнительно высоких частотах электромагнитного поля (оптические колебания видимого и инфракрасного спектров), что приводит к слабому поглощению такого излучения в веществе.
16)Поляризованность - ?
Векторная величина, характеризующая степень электрической поляризации вещества, равная пределу отношения электрического момента, связанного с элементом объема вещества, к объему этого элемента, когда объем и все размеры этого элемента объема стремятся к нулю
Для количественного описания поляризации диэлектрика пользуются векторной величиной —поляризованностью,определяемой как дипольный момент единицы объема диэлектрика:
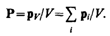
17)Напряженность электрического поля в диэлектрике
В соответствии с принципом суперпозиции электрическое поле в диэлектрике векторно складывается из внешнего поля 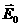 и поля поляризационных зарядов
и поля поляризационных зарядов 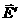 (рис.3.11).
(рис.3.11).
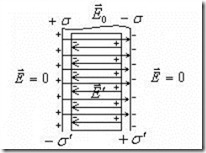
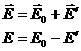 или по абсолютной величине
или по абсолютной величине
Мы видим, что величина напряженности поля 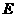 в диэлектрике меньше, чем вакууме. Другими словами, любой диэлектрик ослабляет внешнее электрическое поле.
в диэлектрике меньше, чем вакууме. Другими словами, любой диэлектрик ослабляет внешнее электрическое поле.
Рис.3.11. Электрическое поле в диэлектрике.
Индукция электрического поля 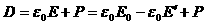 , где
, где 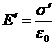 ,
, 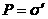 , то есть
, то есть 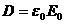 . С другой стороны,
. С другой стороны, 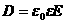 , откуда находим, что ε0Е0 = ε0εЕ и, следовательно, напряженность электрического поля в изотропном диэлектрике есть:
, откуда находим, что ε0Е0 = ε0εЕ и, следовательно, напряженность электрического поля в изотропном диэлектрике есть:
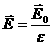
Эта формула раскрывает физический смысл диэлектрической проницаемости и показывает, что напряженность электрического поля в диэлектрике в 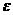 разменьше, чем в вакууме. Отсюда следует простое правило: чтобы написать формулы электростатики в диэлектрике, надо в соответствующих формулах электростатики вакуума рядом с
разменьше, чем в вакууме. Отсюда следует простое правило: чтобы написать формулы электростатики в диэлектрике, надо в соответствующих формулах электростатики вакуума рядом с 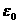 приписать
приписать 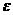 .
.
В частности, закон Кулона в скалярной форме запишется в виде:
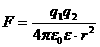
18)Диэлектрическая проницаемость вещества
Газы
Поляризация газа может чисто электронной или дипольной, если молекулы газа обладают дипольным моментом.
Газы имеют малые плотности из-за больших расстояний между молекулами. Поэтому поляризация газов незначительная и диэлектрическая проницаемость газов ε при нормальном давлении близка к 1.
Диэлектрическая проницаемость газов растет с ростом радиуса молекулы, поскольку из-за роста радиуса возрастает поляризуемость молекулы Зависимость диэлектрической проницаемости газов от давления p и температуры T определяется изменением концентрации молекул n.
p = nkT.
Здесь k - постоянная Больцмана.
Жидкие диэлектрики
Для неполярных жидкостей ε невелика и близка к значению квадрата показателя преломления света n
ε = n2
Для нейтральных жидкостей ε уменьшается с ростом температуры, что связано с уменьшением плотности жидкости с ростом температуры, а, значит, и уменьшением концентрации молекул.
Для бензола, толуола ε = n2 ≈ 2.
В дипольных (полярных) жидкостях одновременно протекают и электронная, и дипольно – релаксационная поляризации. ε тем больше, чем больше электрический момент диполей μ и чем больше число молекул в единице объема. Диэлектрическая проницаемость полярных жидкостей больше чем у неполярных. Например, ε касторового масла = 4,5.
Температурная зависимость ε полярных жидкостей характеризуется дипольным максимумом в области резкого изменения вязкости жидкости. С ростом частоты электрическогополядиэлектрическая проницаемость полярных жидкостей снижается до значений, определяемых электронной поляризацией.
ε(ω)ω→∞= n2
Твердые диэлектрики
В твердых диэлектриках возможны все виды поляризации.
Для нейтральных диэлектриков ε = n2, что подтверждается ниже приведенными результатами для неполярных диэлектриков при температуре 20 ºС
Ионные кристаллы с плотной упаковкой частиц обладают электронной и ионной поляризацией. ε изменяется в широких диапазонах. С ростом температуры ε обычно растет. В неорганических аморфных диэлектриках (стеклах) ε изменяется в пределах от 4 до 20, возрастает с ростом температуры, хотя в ряде случаев (рутил TiO2, титанат кальцияCaTiO3) может и уменьшаться.
Органические полярные диэлектрики имеют дипольно – релаксационную поляризацию. ε изменяется в широких пределах, но обычно имеет значение 4 – 10. Диэлектрическая проницаемость зависит от температуры, частоты приложенного напряжения, подчиняясь, в целом, закономерностям, проявляющимся у полярных жидкостей.
19)Теорема Гаусса для электростатического поля в диэлектрике
Для описания электрического поля, в частности, в диэлектрике, вводят в рассмотрение вектор электрического смещения (вектор электростатической индукции) 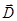 , равный
, равный
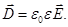
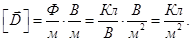
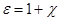
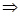
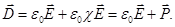
Результирующее поле в диэлектрике описывается вектором напряженности 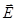 .
. 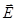 зависит от свойств диэлектрика (от ε). Вектором
зависит от свойств диэлектрика (от ε). Вектором 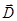 описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать перераспределение свободных зарядов, создающих поле. Поэтому вектор
описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать перераспределение свободных зарядов, создающих поле. Поэтому вектор 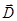 характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
Силовые линии вектора 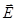 могут начинаться и заканчиваться как на свободных, так и на связанных зарядах. Силовые линии вектора
могут начинаться и заканчиваться как на свободных, так и на связанных зарядах. Силовые линии вектора 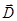 - только на свободных. Через области поля, где находятся связанные заряды, силовые линии вектора
- только на свободных. Через области поля, где находятся связанные заряды, силовые линии вектора