Энтропия. закон возрастания энтропии.

Как мы уже отмечали, система находится большую часть времени в микросостояниях с энергией, близкой к наиболее вероятному значению Е_в . Очевидно, что отклонения энергии системы от Е_в практически не выходят за интервал 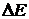, соответствующий энергетической “ширине” функции Р(Е) (см. рис. §39). Чем больше 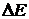, тем большие отклонения может испытывать энергия системы, а, следовательно, и другие макровеличины, характеризующие систему. Таким образом, величина 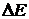служит характеристикой состояния системы.

Вместо интервала энергии 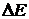, малого, как следует из изложенных ранее соображений, состояние системы можно характеризовать числом микросостояний DГ

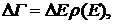
соответствующих “ширине” пика зависимости Р(Е). Величина DГ - есть число микросостояний, которое соответствует одному и тому же макросостоянию с энергией Е_в. DГ - называется статистическим весом, а величина

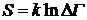
называется энтропией.

Чем больше DГ, тем больше возможных микросостояний доступно системе, следовательно, тем больше неопределенность того, в каком микросостоянии находится система. Можно сказать, что энтропия есть мера неопределенности микросостояния системы. Если система состоит из двух подсистем (тел), статистические веса которых DГ₁ и DГ₂ , то вследствие мультипликативности статистический вес всей системы DГ = DГ₁DГ₂, и тогда энтропия всей системы

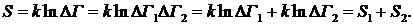
Энтропия системы есть сумма энтропий входящих в нее подсистем; энтропия есть аддитивная величина. Понятие энтропии имеет смысл только для макроскопических систем, содержащих большое число частиц; бессмысленно, например, говорить об энтропии одного атома, молекулы.

Вернемся к понятию равновесного состояния. Равновесным является такое макросостояние системы, которое не имеет тенденции к изменению с течением времени.Ясно, что отсутствие такой тенденции будет сильнее всего выражено у наиболее вероятного из всех макросостояний. Вероятность состояния пропорциональна статистическому весу. Поэтому равновесное состояние изолированной системы можно определить как состояние, статистический вес которого максимален. Замкнутая система, выведенная из состояния равновесия и предоставленная сама себе, с течением времени возвращается в состояние полного равновесия. Этот переход сопровождается таким изменением макроскопического состояния, чтобы число соответствующих ему микросостояний увеличивалось.Итак, неравновесная замкнутая система непрерывно переходит из состояния с меньшей энтропией в состояние с большей энтропией, пока энтропия не достигнет максимального значения, соответствующего состоянию статистического равновесия. Это утверждение называется законом возрастания энтропии (вторым началом термодинамики).

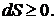
Закон возрастания энтропии можно интерпретировать и иначе: если в какой-то момент времени энтропия замкнутой системы имеет определенное значение, то в последующие моменты энтропия будет либо возрастать (переход от неравновесного состояния к равновесному состоянию), либо оставаться постоянной (равновесное состояние). Обратный ход событий, т.е. уменьшение энтропии в замкнутой системе, практически невероятен. Поэтому процессы, при которых энтропия замкнутой системы возрастает, называются необратимыми. Процессы, при которых энтропия сохраняется, могут идти и в обратном направлении и являются, следовательно, обратимыми. Отметим еще раз, что закон возрастания энтропии (точнее - не убывания) применим лишь к замкнутым системам. В незамкнутых системах энтропия может и убывать.