Идеальный газ. Статистическое уравнение идеального газа.

Статистическая физика и термодинамика. Основные понятия

Статистической физики.

Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества исходя из так называемых молекулярно-кинетических представлений. Согласно этим представлениям, любое тело - твердое, жидкое или газообразное - состоит из большого количества весьма малых обособленных частиц - молекул. Молекулы всякого вещества находятся в беспорядочном, хаотическом движении. Его интенсивность зависит от температуры вещества. Непосредственным доказательством существования хаотического движения молекул служит броуновское движение. Это явление заключается в том, что весьма малые (видимые только в микроскоп) взвешенные в жидкости частицы всегда находятся в состоянии непрерывного беспорядочного движения, которое не зависит от внешних причин и оказывается проявлением внутреннего движения веществ. Броуновские частицы совершают движение под действием беспорядочных ударов молекул.

Молекулярно-кинетическая теория ставит себе целью истолковать те свойства тел, которые непосредственно наблюдаются на опыте (давление, температура и т.п.) как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь такими средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое ее название - статистическая физика.

Изучением различных свойств тел и изменений состояния вещества занимается также термодинамика. Однако, в отличии от молекулярно-кинетической теории термодинамикаизучает макроскопические свойства тел и явлений природы, не интересуясь их микроскопической картиной. Не вводя в рассмотрение молекулы и атомы, не входя в рассмотрение процессов, термодинамика позволяет делать целый ряд выводов относительно их протекания.

В основе термодинамики лежит несколько фундаментальных законов ( называемых началами термодинамики), установленных на основании обобщения большой совокупности опытных фактов. В силу этого выводы термодинамики имеют весьма общий характер.

Подходя к рассмотрению изменений состояний вещества с различных точек зрения, термодинамика и молекулярно - кинетическая теория взаимно дополняют друг друга, образуя по существу одно целое.

Основные понятия статистической физики. Сформулируем основные определения, используемые в статистической физике.

Система - совокупность взаимодействующих частиц ( например, молекулы в сосуде, ядра и электроны в кристалле и др.).

Замкнутая система - не взаимодействующая с окружающей средой система; обмен энергией между замкнутой системой и средой отсутствует. Энергия замкнутой системы неизменна.

Подсистема (квазинезависимая система) - часть системы, слабо взаимодействующая с остальными частями системы. Взаимодействие считается слабым, если средняя энергия взаимодействия (т.е. доля энергии, которая может быть отдана или принята подсистемой при взаимодействии) много меньше всей энергии подсистемы.

Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом и т.д. Подобные величины, характеризующие состояние системы, называются параметрами состояния ( или макропараметрами).

Соотношение, определяющее связь между параметрами какой-либо системы, называется уравнением состояния этой системы.

Микроскопическая величина - величина, сопоставимая с размерами структурных элементовсистемы.

Макроскопическая величина - величина, значительно большая размеров структурных элементов системы.

Микроскопическое состояние (микросостояние) - состояние системы или подсистемы, для которого указаны состояния (микропараметры) всех структурных элементов, допускаемые законами механики.

Макроскопическое состояние (макросостояние) - состояние системы или подсистемы, заданное с помощью величин - макропараметров, которые могут быть определены макроскопическими измерениями ( например, объем, давление, температура).

Равновесное состояние ( статистическое равновесие, термодинамическое равновесие) - макроскопическое состояние, которое не меняется со временем, за исключением флуктуаций.

Флуктуации - случайные,”самопроизвольные”, отклонения измеряемых значений физических величин от их средних значений.

Эргодическая гипотеза.

Напомним еще раз, что статистическая физика ставит задачей определять средние значения макропараметров и устанавливать взаимосвязь между ними в зависимости от строения системы и характера взаимодействия частиц, составляющих систему.

Для определения среднего значения некоторой величины ¦ есть два способа. Можно, во-первых, проследить за ходом изменения величины ¦ во времени, т.е. определить ¦(t), а затем найти среднее

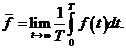(33.1)

Обычно именно таким путем осуществляется опытное определение физических величин, процедуру усреднения выполняет измерительный прибор.При теоретическом расчете среднего 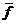функция ¦( t ) неизвестна. Статистическая физика определяет значение макропараметра 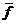через вероятность пребывания макросистемы в различных доступных ей микросостояниях.

Пусть вероятность обнаружения системы в микросостояние с энергией Е_i составляет Р(Е_i) , и физическая величина ¦ при этом имеет значение ¦_i . Тогда среднее значение 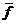по известному из теории вероятности соотношению определяется

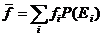(33.2)

Сумма в (33.2) вычисляется по всем доступным системе микросостояниям. Заметим, что одному значению энергии Е_i могут соответствовать несколько микросостояний, их число обозначим Г(Е_i). Величина Г(Е_i) называется статистическим весом.

Представьте,например, несколько газовых молекул в сосуде (см. рисунок). Вследствие неразличимости молекул их определенное распределение по частям сосуда ( одна молекула в левой части сосуда и две молекулы в правой части) может быть осуществлено несколькими, Г(Е_i) способами . В данном примере Г(Е_i) = 3.

Статистическая физика исходит из следующего предположения, известного под названием эргодической гипотезы:замкнутая макросистема за большой промежуток времени побывает во всех доступных ей микросостояниях, причем эти микросостояния равновероятны. Иначе, для макросистемы среднее значение макровеличины ¦ за большой отрезок времени совпадает со средним значением этой величины по большому ансамблю идентичных макросистем, т.е. 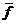, найденное по (33.1) и (33.2), одинаково.

Процедура нахождения 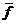путем суммирования (33.2) называется статистическим усреднением: для усреднения необходима функция Р(Е) - функция статистического распределения ( или просто функция распределения). Если эта функция известна, то в соответствии с (33.2) можно рассчитать все характеристики макросостояния. Дальнейшая задача состоит в нахождении функции статистического распределения.

Распределение Гиббса.

Будем рассматривать системы в равновесном состоянии. Функция распределения таких систем не должна зависеть от времени.

Пусть имеем замкнутую макросистему. Каждому дискретному значению Е_i энергии системы может отвечать некоторая группа микросостояний Г(Е_i). Поскольку все микросостояния с заданной энергией равноправны, вероятность обнаружить систему в состоянии с энергией Е_i пропорциональна числу микросостояний

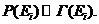(34.1)

Это соотношение называется микроканоническим распределением Гиббса.Замкнутых систем, строго говоря, в природе не существует, реальные системы всегда в какой - либо мере открыты. Рассмотрим макросистему А, находящуюся в контакте с большой системой В - термостатом.

Система А открытая, она может обмениваться энергией с системой В. Предположим, что системы А и В образуют вместе замкнутую систему АВ. Для замкнутой системы АВ энергия постоянна

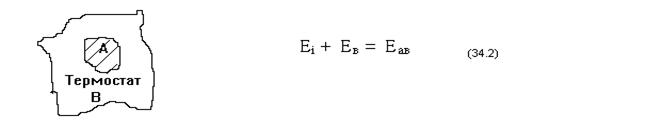
Сумма ( 34.2 ) показывает аддитивность системы:энергия составной системы АВ равна сумме энергий подсистем А и В (энергией взаимодействия подсистем пренебрегаем).

Вероятность обнаружить открытую систему А в состоянии с энергией Е_i , а систему В с энергией Е_в, как вероятность сложного события, равна произведению вероятностей Р(Е_i)Р(Е_в). В то же время составная система АВ - замкнутая, поэтому для нее справедливо микроканоническое распределение

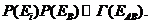( 34.3)

Заметим, что под системой В мы понимаем очень большую систему, так что Е_в>> Е_i . Поэтому, каково бы ни было изменение состояния системы А, состояние системы В можно считать практически неизменным, Р( Е_в ) = const. Кроме того, число микросостояний составной системы обладает, в отличии от энергии, свойством мультипликативности, так что

Г ( Е_АВ) = Г ( Е_В ) Г ( Е_i ) . ( 34.4 )

Поясним это на примере. Пусть в системе А состояние с энергией Е₁ реализуется двумя способами (Г (Е₁) = 2), а в системе В состояние с энергией Е₂ - тремя способами ( Г (Е₂) = 3). Макросостояние объединенной системы АВ с энергией Е₁ + Е₂ осуществляется , например, если система А находится в первом микросостоянии, а система В - либо в первом, либо во втором, либо в третьем микросостоянии и т.д. Следовательно, макросостояние системы АВ с энергией Е₁ + Е₂ может быть осуществлено Г(Е₁) Г(Е₂) = 2·3= = 6 способами.

Тогда, с учетом (34.4) и Р(Е_В) = сonst, (34.5) перепишем в виде

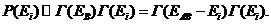( 34.5 )

Выразим далее функцию Г ( Е_АВ- Е_i ) через энергию Е_i системы А. При этом надо иметь ввиду, что энергия и число микросостояний обладают совершенно различными свойствами: энергия аддитивна, число микросостояний мультипликативно. Этим свойствам можно удовлетворить, если представить

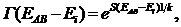( 34.6)

здесь S(E_AB- E_i) - некоторая новая функция аргумента Е_i; k - постоянная Больцмана. Функция S , как и энергия, аддитивна.

Поскольку предполагается Е_i<< Е_АВ , функцию S можно разложить в ряд по степеням малой энергии Е_i и ограничиться первыми членами разложения

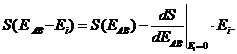(34.7)

Обозначим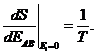

Тогдаполучим

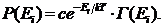( 34.8 )

Выражение (34.8) есть функция статистического распределения открытой системы или каноническое распределение Гиббса:оно определяет вероятность обнаружить систему, способную слабо обмениваться энергией с большой системой в одном из Г(E_i) микросостояний с энергией Е_i (число частиц в системе предполагается неизменным). Распределение Гиббса - важнейшее в современной физике.Оно включает в себя многие частные распределения, например, Максвелла, Больцмана, Ферми-Дирака и др.

В коэффициент с в (34.8) включены все множители, не зависящие от свойств системы А (например, множитель exp[S(E_AB)/k]). Он определяется из условия нормировки: сумма вероятностей всех доступных подсистеме состояний равна единице å Р(Е_i ) = 1, откуда

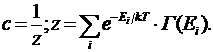(34.9)

В системах, состоящих из большого числа частиц, уровни энергии Е_i расположены столь близко друг к другу, что дискретностью состояний можно пренебречь. Иначе, системе доступны любые непрерывно изменяющиеся значения энергии. Такие системы называются классическими. В случае классической системы можно в (34.8) перейти от суммирования к интегрированию. Для этого разбивают весь интервал энергии на одинаковые малые составляющие dЕ. В пределах каждого малого интервала dE значение экспоненты exp(-E_i/k T) можно считать неизменными. Число микросостояний в интервале энергий dE пропорционально величине этого интервала, т.е. dГ = r (Е) dE. Здесь r(Е) = dГ/dE - плотность микросостояний (их число, приходящееся на единичный интервал энергии в окрестностях значения Е). Таким образом, в классическом пределе каждое слагаемое в сумме (34.9) должно быть заменено на

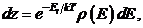
а суммирование на интегрирование

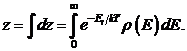(34.10)

Статистический интеграл (34.10) и сумма (34.9) имеют принципиальное значение в физике. Оказывается, одного их значения достаточно для расчета средних значений любых макропараметров.

Вероятность обнаружить классическую систему в любом из микросостояний с энергией от Е до Е + dЕ , по аналогии с (34.8), составляет

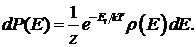(34.11)

Плотность вероятности

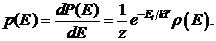(34.12)

В приведенных выше формулах и распределениях предполагалось, что число частиц в системе неизменно. Это ограничение можно было бы снять и получить распределение Гиббса для системы с переменным числом частиц - так называемое большое каноническое распределение Гиббса. Одним из параметров канонического распределения Гиббса является

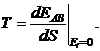(34.13)

T -есть статистическая температура. Иногда статистической температурой называют произведение kT.

Статистическая физика и термодинамика. Основные понятия

Статистической физики.

Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества исходя из так называемых молекулярно-кинетических представлений. Согласно этим представлениям, любое тело - твердое, жидкое или газообразное - состоит из большого количества весьма малых обособленных частиц - молекул. Молекулы всякого вещества находятся в беспорядочном, хаотическом движении. Его интенсивность зависит от температуры вещества. Непосредственным доказательством существования хаотического движения молекул служит броуновское движение. Это явление заключается в том, что весьма малые (видимые только в микроскоп) взвешенные в жидкости частицы всегда находятся в состоянии непрерывного беспорядочного движения, которое не зависит от внешних причин и оказывается проявлением внутреннего движения веществ. Броуновские частицы совершают движение под действием беспорядочных ударов молекул.

Молекулярно-кинетическая теория ставит себе целью истолковать те свойства тел, которые непосредственно наблюдаются на опыте (давление, температура и т.п.) как суммарный результат действия молекул. При этом она пользуется статистическим методом, интересуясь не движением отдельных молекул, а лишь такими средними величинами, которые характеризуют движение огромной совокупности частиц. Отсюда другое ее название - статистическая физика.

Изучением различных свойств тел и изменений состояния вещества занимается также термодинамика. Однако, в отличии от молекулярно-кинетической теории термодинамикаизучает макроскопические свойства тел и явлений природы, не интересуясь их микроскопической картиной. Не вводя в рассмотрение молекулы и атомы, не входя в рассмотрение процессов, термодинамика позволяет делать целый ряд выводов относительно их протекания.

В основе термодинамики лежит несколько фундаментальных законов ( называемых началами термодинамики), установленных на основании обобщения большой совокупности опытных фактов. В силу этого выводы термодинамики имеют весьма общий характер.

Подходя к рассмотрению изменений состояний вещества с различных точек зрения, термодинамика и молекулярно - кинетическая теория взаимно дополняют друг друга, образуя по существу одно целое.

Основные понятия статистической физики. Сформулируем основные определения, используемые в статистической физике.

Система - совокупность взаимодействующих частиц ( например, молекулы в сосуде, ядра и электроны в кристалле и др.).

Замкнутая система - не взаимодействующая с окружающей средой система; обмен энергией между замкнутой системой и средой отсутствует. Энергия замкнутой системы неизменна.

Подсистема (квазинезависимая система) - часть системы, слабо взаимодействующая с остальными частями системы. Взаимодействие считается слабым, если средняя энергия взаимодействия (т.е. доля энергии, которая может быть отдана или принята подсистемой при взаимодействии) много меньше всей энергии подсистемы.

Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом и т.д. Подобные величины, характеризующие состояние системы, называются параметрами состояния ( или макропараметрами).

Соотношение, определяющее связь между параметрами какой-либо системы, называется уравнением состояния этой системы.

Микроскопическая величина - величина, сопоставимая с размерами структурных элементовсистемы.

Макроскопическая величина - величина, значительно большая размеров структурных элементов системы.

Микроскопическое состояние (микросостояние) - состояние системы или подсистемы, для которого указаны состояния (микропараметры) всех структурных элементов, допускаемые законами механики.

Макроскопическое состояние (макросостояние) - состояние системы или подсистемы, заданное с помощью величин - макропараметров, которые могут быть определены макроскопическими измерениями ( например, объем, давление, температура).

Равновесное состояние ( статистическое равновесие, термодинамическое равновесие) - макроскопическое состояние, которое не меняется со временем, за исключением флуктуаций.

Флуктуации - случайные,”самопроизвольные”, отклонения измеряемых значений физических величин от их средних значений.

Эргодическая гипотеза.

Напомним еще раз, что статистическая физика ставит задачей определять средние значения макропараметров и устанавливать взаимосвязь между ними в зависимости от строения системы и характера взаимодействия частиц, составляющих систему.

Для определения среднего значения некоторой величины ¦ есть два способа. Можно, во-первых, проследить за ходом изменения величины ¦ во времени, т.е. определить ¦(t), а затем найти среднее

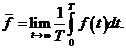(33.1)

Обычно именно таким путем осуществляется опытное определение физических величин, процедуру усреднения выполняет измерительный прибор.При теоретическом расчете среднего 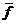функция ¦( t ) неизвестна. Статистическая физика определяет значение макропараметра 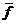через вероятность пребывания макросистемы в различных доступных ей микросостояниях.

Пусть вероятность обнаружения системы в микросостояние с энергией Е_i составляет Р(Е_i) , и физическая величина ¦ при этом имеет значение ¦_i . Тогда среднее значение 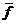по известному из теории вероятности соотношению определяется

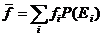(33.2)

Сумма в (33.2) вычисляется по всем доступным системе микросостояниям. Заметим, что одному значению энергии Е_i могут соответствовать несколько микросостояний, их число обозначим Г(Е_i). Величина Г(Е_i) называется статистическим весом.

Представьте,например, несколько газовых молекул в сосуде (см. рисунок). Вследствие неразличимости молекул их определенное распределение по частям сосуда ( одна молекула в левой части сосуда и две молекулы в правой части) может быть осуществлено несколькими, Г(Е_i) способами . В данном примере Г(Е_i) = 3.

Статистическая физика исходит из следующего предположения, известного под названием эргодической гипотезы:замкнутая макросистема за большой промежуток времени побывает во всех доступных ей микросостояниях, причем эти микросостояния равновероятны. Иначе, для макросистемы среднее значение макровеличины ¦ за большой отрезок времени совпадает со средним значением этой величины по большому ансамблю идентичных макросистем, т.е. 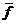, найденное по (33.1) и (33.2), одинаково.

Процедура нахождения 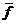путем суммирования (33.2) называется статистическим усреднением: для усреднения необходима функция Р(Е) - функция статистического распределения ( или просто функция распределения). Если эта функция известна, то в соответствии с (33.2) можно рассчитать все характеристики макросостояния. Дальнейшая задача состоит в нахождении функции статистического распределения.

Распределение Гиббса.

Будем рассматривать системы в равновесном состоянии. Функция распределения таких систем не должна зависеть от времени.

Пусть имеем замкнутую макросистему. Каждому дискретному значению Е_i энергии системы может отвечать некоторая группа микросостояний Г(Е_i). Поскольку все микросостояния с заданной энергией равноправны, вероятность обнаружить систему в состоянии с энергией Е_i пропорциональна числу микросостояний

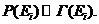(34.1)

Это соотношение называется микроканоническим распределением Гиббса.Замкнутых систем, строго говоря, в природе не существует, реальные системы всегда в какой - либо мере открыты. Рассмотрим макросистему А, находящуюся в контакте с большой системой В - термостатом.

Система А открытая, она может обмениваться энергией с системой В. Предположим, что системы А и В образуют вместе замкнутую систему АВ. Для замкнутой системы АВ энергия постоянна

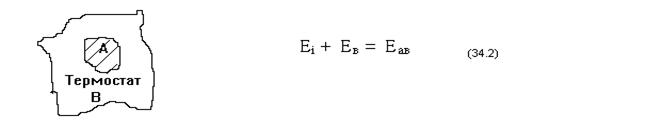
Сумма ( 34.2 ) показывает аддитивность системы:энергия составной системы АВ равна сумме энергий подсистем А и В (энергией взаимодействия подсистем пренебрегаем).

Вероятность обнаружить открытую систему А в состоянии с энергией Е_i , а систему В с энергией Е_в, как вероятность сложного события, равна произведению вероятностей Р(Е_i)Р(Е_в). В то же время составная система АВ - замкнутая, поэтому для нее справедливо микроканоническое распределение

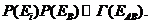( 34.3)

Заметим, что под системой В мы понимаем очень большую систему, так что Е_в>> Е_i . Поэтому, каково бы ни было изменение состояния системы А, состояние системы В можно считать практически неизменным, Р( Е_в ) = const. Кроме того, число микросостояний составной системы обладает, в отличии от энергии, свойством мультипликативности, так что

Г ( Е_АВ) = Г ( Е_В ) Г ( Е_i ) . ( 34.4 )

Поясним это на примере. Пусть в системе А состояние с энергией Е₁ реализуется двумя способами (Г (Е₁) = 2), а в системе В состояние с энергией Е₂ - тремя способами ( Г (Е₂) = 3). Макросостояние объединенной системы АВ с энергией Е₁ + Е₂ осуществляется , например, если система А находится в первом микросостоянии, а система В - либо в первом, либо во втором, либо в третьем микросостоянии и т.д. Следовательно, макросостояние системы АВ с энергией Е₁ + Е₂ может быть осуществлено Г(Е₁) Г(Е₂) = 2·3= = 6 способами.

Тогда, с учетом (34.4) и Р(Е_В) = сonst, (34.5) перепишем в виде

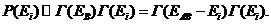( 34.5 )

Выразим далее функцию Г ( Е_АВ- Е_i ) через энергию Е_i системы А. При этом надо иметь ввиду, что энергия и число микросостояний обладают совершенно различными свойствами: энергия аддитивна, число микросостояний мультипликативно. Этим свойствам можно удовлетворить, если представить

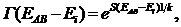( 34.6)

здесь S(E_AB- E_i) - некоторая новая функция аргумента Е_i; k - постоянная Больцмана. Функция S , как и энергия, аддитивна.

Поскольку предполагается Е_i<< Е_АВ , функцию S можно разложить в ряд по степеням малой энергии Е_i и ограничиться первыми членами разложения

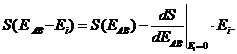(34.7)

Обозначим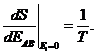

Тогдаполучим

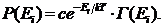( 34.8 )

Выражение (34.8) есть функция статистического распределения открытой системы или каноническое распределение Гиббса:оно определяет вероятность обнаружить систему, способную слабо обмениваться энергией с большой системой в одном из Г(E_i) микросостояний с энергией Е_i (число частиц в системе предполагается неизменным). Распределение Гиббса - важнейшее в современной физике.Оно включает в себя многие частные распределения, например, Максвелла, Больцмана, Ферми-Дирака и др.

В коэффициент с в (34.8) включены все множители, не зависящие от свойств системы А (например, множитель exp[S(E_AB)/k]). Он определяется из условия нормировки: сумма вероятностей всех доступных подсистеме состояний равна единице å Р(Е_i ) = 1, откуда

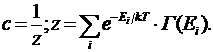(34.9)

В системах, состоящих из большого числа частиц, уровни энергии Е_i расположены столь близко друг к другу, что дискретностью состояний можно пренебречь. Иначе, системе доступны любые непрерывно изменяющиеся значения энергии. Такие системы называются классическими. В случае классической системы можно в (34.8) перейти от суммирования к интегрированию. Для этого разбивают весь интервал энергии на одинаковые малые составляющие dЕ. В пределах каждого малого интервала dE значение экспоненты exp(-E_i/k T) можно считать неизменными. Число микросостояний в интервале энергий dE пропорционально величине этого интервала, т.е. dГ = r (Е) dE. Здесь r(Е) = dГ/dE - плотность микросостояний (их число, приходящееся на единичный интервал энергии в окрестностях значения Е). Таким образом, в классическом пределе каждое слагаемое в сумме (34.9) должно быть заменено на

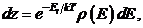
а суммирование на интегрирование

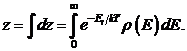(34.10)

Статистический интеграл (34.10) и сумма (34.9) имеют принципиальное значение в физике. Оказывается, одного их значения достаточно для расчета средних значений любых макропараметров.

Вероятность обнаружить классическую систему в любом из микросостояний с энергией от Е до Е + dЕ , по аналогии с (34.8), составляет

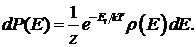(34.11)

Плотность вероятности

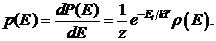(34.12)

В приведенных выше формулах и распределениях предполагалось, что число частиц в системе неизменно. Это ограничение можно было бы снять и получить распределение Гиббса для системы с переменным числом частиц - так называемое большое каноническое распределение Гиббса. Одним из параметров канонического распределения Гиббса является

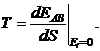(34.13)

T -есть статистическая температура. Иногда статистической температурой называют произведение kT.

Идеальный газ. Статистическое уравнение идеального газа.

Одним из объектов статистической физики является идеальный газ - совокупность частиц, слабо взаимодействующих между собой: средняя за большой отрезок времени энергия взаимодействия частицы с другими частицами много меньше средней собственной энергии частицы.

Не следует считать, что понятие идеального газа применимо лишь к газообразному состоянию вещества; это понятие гораздо шире. Так, колебания кристаллической решетки твердого тела под действием теплового возбуждения во многих случаях удовлетворяет модели идеального газа (газ фононов). Совокупность электронов проводимости в металлах или полупроводниках при некоторых условиях можно также рассматривать как идеальный (электронный) газ.

Чем слабее взаимодействие между частицами, тем ближе ансамбль частиц к идеальному газу. Наличие взаимодействия, однако, принципиально необходимо для установления статистического равновесия. Взаимодействие должно быть слабым лишь на столько, чтобы при расчетах, включающих собственные энергии частиц, энергией взаимодействия можно было бы пренебречь.

Основными макропараметрами идеального газа являются:

Объем V [м³] - часть пространства в которой двигаются газовые молекулы.

Давление Р = ¶F_n/¶S [н/м² = Па] - отношение силы ¶F_n , перпендикулярной к площадке ¶S, к размеру площадки.

Температура T [ K ] - параметр, физический смысл которого обсуждается далее.

Для характеристики масс атомов и молекул применяются величины, получившие название относительной атомной массы (атомная масса) и относительной молекулярной массы вещества (молекулярной массы).

Атомной массой химического элемента называется отношение массы атома этого элемента к 1/12 массы атома ¹²С углерода ( точнее изотопа углерода с массовым числом 12).

Молекулярной массой вещества называется отношение массы молекулы этого вещества к 1/12 массы атома углерода ¹² С.

Количество вещества, в котором содержится число частиц ( атомов, молекул, ионов, электронов и т.д.), равное числу атомов в 0,012 кг изотопа углерода ¹²С, называется молем.

Число частиц, содержащихся в одном моле вещества, называется числом Авогадро. Опытным путем найдено, что

N_A = 6,022 10²³ моль ^-1.

Массу моля называют молярной массой m.

Представим, что газ заключен в сосуд в форме прямоугольного параллелепипеда, стенки сосуда являются идеально отражающими (т.е. молекулы отскакивают от стенок под тем же углом, под которым они сталкиваются с ним; при этом абсолютные значения скоростей не меняются). Найдем давление газа на одну из граней, например АВСД.При отражении от грани АВСД любой, допустим, i -й молекулы, имеющейсоставляющую скорости V_{i x} по оси х,грани передается импульс 2mV_{i x} ; m - масса молекулы. Между двумяпоследовательными столкновениямис гранью молекула двигается как свободная и возвращается к грани через время Dt=2L/V_{i x}.Следовательно, за 1 с каждая молекула сталкивается с рассматриваемой гранью V_{i x} / 2Lраз и передает ей импульс 2mV_{i x} (V_{i x}/2L) = mV_{i x}²/L. Результирующая сила F_x , действующая на стенку, по второму закону Ньютона равна импульсу, полученному стенкой за 1 секунду от всех N молекул газа

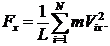(35.1)

Все направления по отношению к газу равноценны, поэтому для большого N

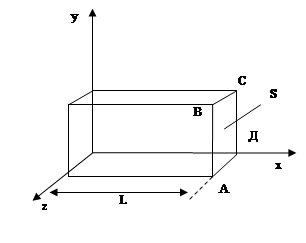
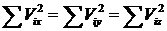(35.2)

Также имеем

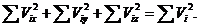
Откуда с учетом (37.2) получаем

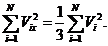(35.3)

Определим среднюю квадратичную (квадратическую) скорость 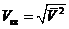соотношением

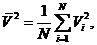
иначе

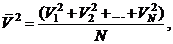
тогда, из (35.1) получаем

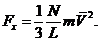
C учетом того, что LS = V, a F_x = p S, окончательно получаем

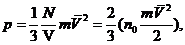(35.4)

где n₀ = N/V - плотность (концентрация) молекул. Величина

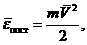(35.5)

есть средняя кинетическая энергия поступательного движения молекул, поэтому

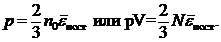(35.6)

Уравнение (35.6) называется основным уравнением молекулярно-кинетической теории идеального газа: давление газа равно двум третьим плотности энергии поступательного движения молекул. Это уравнение носит универсальный характер - в него не входят величины, которые бы зависели от природы газа. Действительно, при обосновании уравнений газ был лишен каких-либо “индивидуальностей”.

С другой стороны, опытное уравнение состояния идеального газа - уравнение Менделеева-Клайперона.

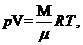(35.7)

где М - масса газа, R = 8,31 дж/моль К - газовая постоянная.

Представляя М =mN и m = m N_A, имеем

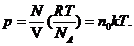(35.8)

Сопоставляя уравнения (35.6) и (35.8), относящиеся к одному объекту - идеальному газу, находим

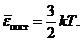(35.9)

Следовательно, энергия 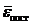определяется только температурой газа; она не зависит от массы молекул, их структуры и других факторов. Вместе с тем, это соотношение дает одно из статистических определений температуры (здесь - молекулярно-кинетическое): температура есть мера средней энергии поступательного движения молекул (в классической теории - не только поступательного, но и других движений, например, вращательного, колебательного).

Зная температуру газа из (35.5) и (35.9) , получаем для средней квадратичной скорости

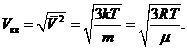(35.10)

В действительности молекулы имеют различные скорости, как большие, так и меньшие квадратичной. Распределение молекул по скоростям впервые установлено Д.Максвеллом.