Интегрирование методом подстановки

Метод интегрирования подстановкойили метод замены переменной заключается во введении новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки).

Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Метод подстановки основан на следующей теореме.

Т.4.1. (замена переменной в неопределенном интеграле)

Пусть функция x = φ(t) определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула

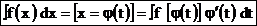(1)

Формула (1) называется формулой замены переменной в неопределенном интегралеили формулой интегрирования подстановкой. После нахождения интеграла в правой части этого равенства следует вернуться от новой переменной t назад к старой переменной х.

Пример.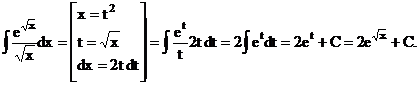

Замечание

Иногда целесообразно подбирать подстановку в виде t = φ(x), тогда формула замены переменной примет вид 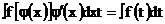, где t = φ(x). Другими словами, формулу (1) можно применять справа налево.

Пример.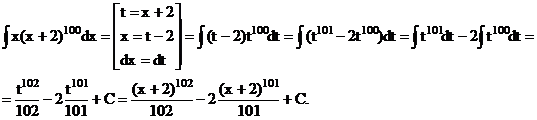

Пример. .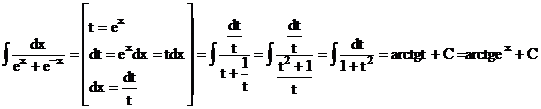

Интегрирование по частям

Таблица интегралов не содержит формул для вычисления интеграла от произведения двух функций, от логарифмической и обратных тригонометрических функций. Эти интегралы находятся методом интегрирования по частям.

Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.

Данный метод базируется на следующей теореме.

Т.4.2. (интегрирование по частям в неопределенном интеграле)

Пусть функции u = u(x) и v = v(x) определены и дифференцируемы на некотором промежутке Х. Если на этом промежутке существует интеграл òv(x)u′(x)dx, то на нем существует и интеграл

òu(x)v′(x)dx, причем справедливо равенство

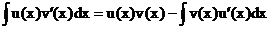(2)

Формула (2) называется формулой интегрирования по частям в неопределенном интеграле.

Так как v′(x)dx = dv и u′(x)dx = du, то формулу (2) можно записать в виде

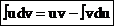. (3)

Формула (3) – формула интегрирования по частям –позволяет свести вычисление интеграла òudv к вычислению интеграла òvdu, который может оказаться существенно более простым, чем исходный.

Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей u и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям (3). Иногда эту формулу приходиться использовать несколько раз.