Вывод формулы Бальмера в теории Бора

Рассматривая первый постулат Бора для перехода водородоподобного иона с орбиты под номером m на орбиту с номером n для энергии излучаемого фотона 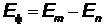, получим:

,

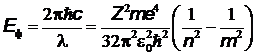откуда ,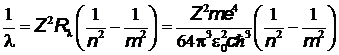

где 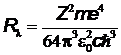- постоянная Ридберга.

Примеры решения задач

Задача 1. Найдите спектральный интервал, в пределах которого расположены линии серии Бальмера атомарного водорода (в длинах волн).

Решение.Формула Бальмера для серии Бальмера имеет вид:

,

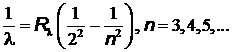где l - длина волны, 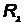= 1,1×10⁷ м^-1 - постоянная Ридберга.

Интервал серии Бальмера ограничен головной линией серии, соответствующей 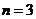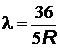= 656 нм и границей серии при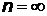 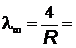365 нм.

Задача 2. Атом водорода находится в возбужденном состоянии с главным квантовым числом 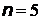. Определите длины волн возможных спектральных линий в спектре атома водорода, наблюдающихся при переходе атома из возбужденных состояний в основное.

Решение.Если атом находится в возбужденном состоянии, характеризующемся главным квантовым числом 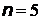, то возможны переходы на уровни, указанные на Рис.11 стрелками:

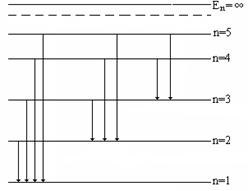четыре линии серии Лаймана (соответствуют переходам 1 – 4), три линии серии Бальмера (соответствует переходам 5 – 7) и две линии серии Пашена (соответствуют переходам 8 -9).

Рис.11 Схема возможных переходов с уровня n = 5

В соответствии с обобщенной формулой Бальмера 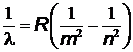, для каждой из этих линий получим:

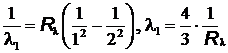= 121 нм, 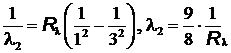= 102 нм.

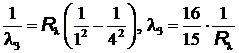= 97 нм, 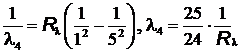= 95 нм,

.

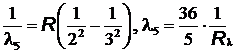= 654 нм, 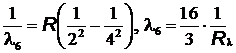= 485 нм,

.

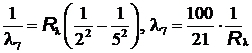= 433 нм, 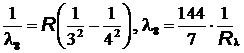= 1870 нм

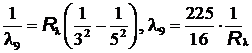= 1280 нм.

Задача 3. Покоившийся атом водорода испустил фотон, соответствующий головной линии серии Лаймана. Найдите скорость отдачи, которую получил атом.

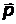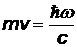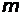Решение.В соответствии с законом сохранения импульса атом приобрел импульс , равный импульсу вылетевшего из него фотона: , где - масса атома. Частота испущенного фотона равна 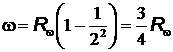, откуда скорость отдачи атома

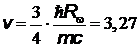м/с.

Задача 4. Определите потенциал ионизации атома водорода.

Решение.Потенциал ионизации 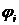- наименьшая разность потенциалов, которую должен пройти электрон в ускоряющем электрическом поле, чтобы его энергии 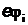при столкновении с невозбужденным атомом было достаточно, чтобы провести его ионизацию. 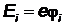. В теории Бора ионизации соответствует переход электрона в атоме из основного состояния в состояние с минимальной кинетической энергией E=0. Энергия электрона при таком переходе увеличивается на величину

DE=0 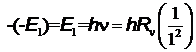. Тогда, энергия ионизации 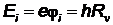, откуда

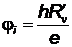= 13,6 В.

Задача 5.Определите первый потенциал возбуждения атома водорода.

Решение.Первый потенциал 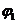возбуждения – наименьшая разность потен-

циалов, которую должен пройти электрон в ускоряющем электрическом поле, чтобы при столкновении с невозбужденном атомом перевести его в первое возбужденное состояние. Для атома водорода – это переход с первой боровской орбиты на вторую c увеличением энергии на 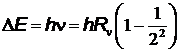за счет энергии бомбардирующего электрона, равной 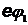. Записывая закон сохранения энергии ,

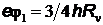получим:

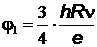= 10,2 В

II. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ

Волны де Бройля.

В одних явлениях (интерференция, дифракция, дисперсия и т.д.) свет проявляет волновые свойства, а в других (фотоэффект, эффект Комптона и др.) ведет себя как поток частиц – фотонов. Эти особенности света называют корпускулярно–волновым дуализмом. Луи де Бройль предположил, что такой дуализм имеет универсальный характер и присущ всем микрочастицам – электронам, протонам, атомам и т.д., т.е. они, наряду с корпускулярными, обладают также и волновыми свойствами. Волны, связанные со свободно движущимися частицами, получили названиеволн де Бройля. Волновые свойства электрона были впервые обнаружены в 1927 году в опытах Девиссона и Джермера по рассеянию электронов на поверхности металлов, где наблюдалась их дифракция. Более наглядными явились опыты Дж.П.Томсона по рассеянию электронов на золотой фольге, схема которых изображена на Рис.12

Рис.12 Схема опытов Дж.П.Томсона по рассеянию электронов

На фотографии (Рис. 13 слева) была получена дифракционная картина, напоминающая дифракцию рентгеновских лучей на оксиде циркония (Рис. 13 справа).

Рис. 13 Дифракционная картина от пучка электронов на золотой фольге (слева) и рентгеновских лучей на оксиде циркония (справа)

Для определения длины волны, частоты и циклической частоты микрочастицы де Бройль использовал соответствующие соотношения для энергии и импульса фотона:

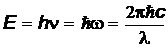и ,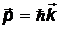

где 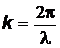- волновое число, а 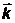–волновой вектор, 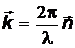( 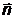–единичный вектор в направлении распространения волны); 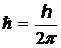–постоянная Планка. Длина волны де Бройля определяется выражением

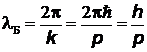
как для релятивистских, так и для нерелятивистских частиц с импульсом .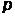

В релятивистском случае выразив импульс частицы 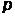через ее полную энер-

гию с помощью соотношения 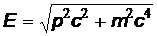, найдем, что

.

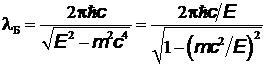Воспользовавшись соотношением для кинетической энергии 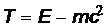, получим формулу: 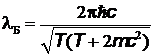, выражающую дебройлевскую длину волны частицы через ее кинетическую энергию. В предельном случае нерелятивистской частицы, когда отношение 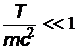получаем выражение для дебройлевской длины волны в нерелятивистском приближении: .

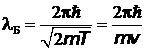Зависимость длины волны де Бройля заряженной частицы, прошедшей ускоряющую разность потенциалов 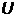, имеет вид:

,

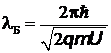где 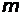–масса частицы; q –заряд частицы.

Первый постулат Бора можно объяснить, используя волны де Бройля. Подставляя в значение 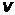, выраженное из формулы 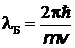получаем 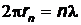. Это соотношение показывает, что стационарными являются лишь те орбиты, на которых укладывается целое число волн де Бройля.

Примеры решения задач

Задача 1. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов 51 В. Найдите длину волны де Бройля этого электрона.

Решение.Пройдяускоряющую разность потенциалов 51 В электрон получает кинетическую энергию 51 эВ, что много меньше его энергии покоя, равной

0,511 МэВ. Поэтому при вычислении длины волны де Бройля 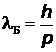импульс электрона берется в нерелятивистском ви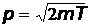де , где 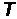- его кинетическая энергия равная 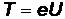. Тогда длина волны де Бройля

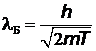=172 пм.

Задача 2. Какой кинетической энергией должен обладать протон, чтобы длина волны де Бройля протона равнялась его комптоновской длине волны?

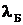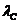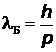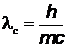Решение.Длина волны де Бройля и комптоновская длина волны определяются по формулам: и , Приравняв 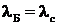, получим 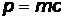, откуда кинетическая энергия протона

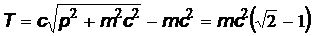= 6,23×10^–11 Дж = 389 МэВ.

Задача 3. Какую энергию 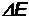необходимо сообщить нерелятивистскому электрону, чтобы его дебройлевская длина волны 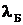уменьшилась в 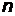раз?

Решение.Пусть конечная длина волны де Бройля равна 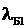. Дебройлевская длина волны электрона связана с его кинетической энергией 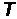следующим образом: 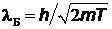. По условию задачи 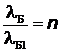, откуд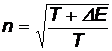а

, а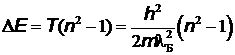

Задача 4. Найдите дебройлевскую длину волны нерелятивистского протона, если в однородном магнитном поле с индукцией 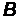радиус кривизны его траектории – окружности – равен .

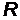Решение.Импульс протона найдем из основного уравнения динамики вращательного движения (под действием силы Лоренца)

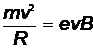
Откуда 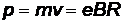, и длина волны де Бройля .

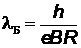7. Соотношения неопределенностей Гейзенберга.

Поскольку микрочастица является волной, определить траекторию ее движения, т.е. одновременно задать ее положение и импульс, не представляется возможным. Неопределенность движения микрочастицы ограничивается соотношениями:

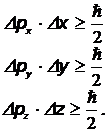
Здесь 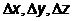– неопределенности координат 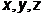; 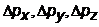–неопределенности проекций импульса частицы на координатные оси; 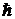–постоянная Планка. Эти соотношения носят название соотношений неопределенностей Гейзенберга.

Таким образом, произведение неопределенностей координаты и соответст-

вующей ей проекции импульса не может быть меньше величины порядка . Следовательно, чем меньше неопределенность одной из величин ( 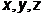или 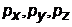), тем больше неопределенность другой. Эти соотношения ограничивают точность одновременного измерения координат и соответствующих проекций импульса частицы.

Если точнее измерить координату микрочастицы , т.е. уменьшать неопределенность 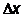, то поскольку процесс измерения обязательно сопровождается неконтролируемым воздействием на микрочастицу со стороны «измерительного прибора», это воздействие увеличивает неопределенность проекции импульса: 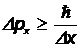. Таким образом, чем точнее определена координата ( 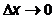), тем менее точно определена проекция 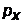( 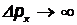), и наоборот. В квантовой механике существует также соотношение неопределенностей для энергии и времени:

,

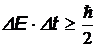где 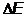–неопределенность энергии некоторого состояния системы; 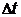-п ромежуток времени, в течение которого оно существует.

Это соотношение означает, что чем короче время существования какого-либо состояния системы, тем больше неопределенность значения энергии этого состояния. Энергетические уровни (дискретные значения энергии) 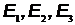и т.д. имеют некоторую ширину (Рис.14), зависящую от среднего времени пребывания системы в

состояниях, соответствующих этим уровням энергии. «Размытость» уровней приводит к неопределенности энергии излучаемого фотона ( 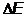) и его частоты ( 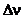) при переходе системы с одного энергетического уровня на другой: 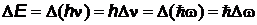. Это проявляется в естественной ширине наблюдаемых спектральных линий.

Как правило, в расчетах вместо точной формулировки используют приближенный вариант запис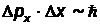и: и 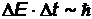, который позволяет получать оценки по порядку величины. Для оценок наименьших возможных значений физических величин (например, энергии) обычно полагают, что 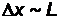(размер системы) и .

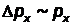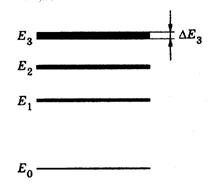
Рис.14 Естественная ширина энергетических уровней

Невозможность одновременно точного определения координаты и соответствующей составляющей импульса не связана с несовершенством методов измерения или измерительных приборов, а является следствием специфики микрочастиц, отражающей особенности их объективных свойств, а именно двойственную корпускулярно–волновую природу. Для описания таких объектов потребовалось создание нового направления в физике – квантовой механики, поскольку в рамках классической физики это оказалось невозможным.

Примеры решения задач

Задача 1.Кинетическая энергия электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопределенностей, оцените минимальные линейные размеры атома.

Решение.Если атом имеет линейные размеры 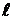, то электрон атома будет на

ходиться в пределах области с неопределенностью 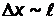и соотношение неопределенности примет вид: ,

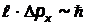откуда .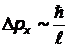

Неопределенность импульса 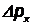равна по порядку величины самому импульсу 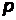, то есть 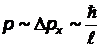. Отсюда

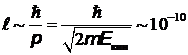м.

где 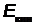- кинетическая энергия электрона.

Задача 2. Электрон с кинетической энергией 4 эВ локализован в области размером 1 мкм. Оцените с помощью соотношения неопределенностей относительную неопределенность его скорости .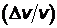

Решение.Неопределенность координаты электрона будем считать равной размерам области локализации электрона: 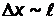, а неопределенность его импульса 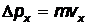. Тогда, исходя из соотношения неопределенностей для координаты и импульса частицы 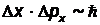, получим для неопределенности модуля скорости электрона 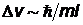, где 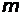- масса электрона. По условию задачи 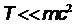, откуда 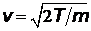. Для относительной неопределенности модуля скорости электрона получаем оценку 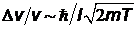~ 10^-4.

Задача 3. Оцените с помощью соотношения неопределенностей минимальную энергию электрона в атоме водорода и его эффективное расстояние от ядра.

Решение.Запишем энергию электрона в атоме водорода как сумму его кине-

тической энергии и потенциальной энергии в поле ядра

,

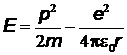где 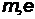- масса и заряд электрона, соответственно, 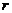- его расстояние от ядра, - электрическая постоянная. Предположим, что неопределенность проекции импульса электрона на некоторую ось (например, на ось 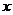) равняется по порядку величины модулю самого импульса электрона 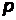, то есть 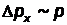, а неопределенность соответствующей координаты 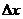по порядку величины равняется , тогда с помощью соотношения неопределенностей для координаты и импульса частицы ( 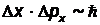) получим оценку 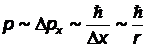и формула для энергии примет вид 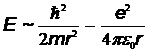. Дифференцируя это выражение по радиусу и приравнивая производную к нулю, находим :

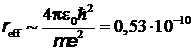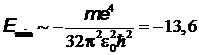м, эВ.

Задача 4. Используя соотношение неопределенности энергии и времени, найдите естественную ширину спектральной линии излучения атома при переходе его из возбужденного состояния в основное. Среднее время жизни атома в возбужденном состоянии равно 10^-8 с, а длина волны излучения - 600 нм.

Решение.При переходе атомов из возбужденного состояния в основное существует некоторая неопределенность в энергии испускаемых фотонов, т.к. энергия возбужденного состояния определенна неточно, и имеет конечную ширину 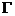(Рис.15). В соответствии с соотношением неопределенности для энергии и времени,

Рис.15 Конечная ширина энергетического уровня

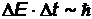.Ширина 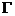энергетического уровня возбужденного состояния связана со средним временем 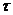жизни атома в этом состоянии соотношением 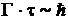. Тогда .

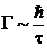Вследствие конечной ширины уровня энергии возбужденного состояния энер

гия фотонов, испускаемых атомами, также имеет разброс, равный ширине энергети-

ческого уровня .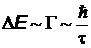

Поскольку энергия фотона связана с длиной волны соотношением 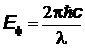, то разбросу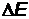 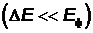энергии соответствует разброс длин волн :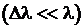

.

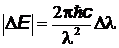Входящий в это выражение конечный интервал длин волн 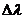и есть естественная ширина спектральной линии.

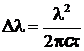=2·10^-14 м.

Относительная неопределенность длины волны равна 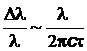~10^-7.