Теория Бора для атома водорода и водородоподобных ионов.

Закономерности атомных спектров

Изучение излучения атомов различных элементов показало, что они состоят из отдельных спектральных линий, расположенных в определенном порядке. В спектре простейшего атома – водорода было обнаружено, что длина волны, частота и циклическая частота спектральных линий определяются обобщенными формулами Бальмера:

, , ,

где м^–1, с^–1, с^–1; – постоянные Ридберга, – длина волны, частота и циклическая частота спектральных линий в спектре атома водорода, соответственно.

Спектральные линии с одинаковым числом 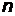( 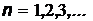) и различными m ( ) образуют спектральную серию, носящую имя исследователя, который обнаружил ее в спектре атома водорода (таблица 1).

Таблица 1. Спектральные серии атома водорода.

Значение	Наименование серии	Значение
	Серия Лаймана в ультрафиолетовой области спектра	2,3,4,…
	Серия Бальмера в видимой области спектра	3,4,5,…
	Серия Пашена в инфракрасной области спектра	4,5,6,…
	Серия Брэккета в инфракрасной области спектра	5,6,7,…

При увеличении 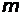длина волны уменьшается, а частота линий увеличивается и достигает предельного значения при . является границей серии. Головная линия серии – линия, соответствующая наименьшей частоте (наибольшей длине волны) в серии при переходе с уровня n + 1 на уровень n.

Спектр поглощения атома водорода при нормальных условиях содержит только одну серию – серию Лаймана. Аналогичный вид имеют и спектры водородоподобных ионов (атомов других элементов таблицы Менделеева с зарядом ядра , у которых удалены все электроны, кроме одного). Это ионы и др.

Z = 1 соответствует атому водорода

Ядерная модель атома.

Экспериментально установив, что в атоме (размером ~10^–10м) имеется ядро (размером ~10^–15м), в котором сосредоточена вся масса атома (99,4%), Резерфорд предложил планетарную модель строения атома. Вокруг ядра с зарядом 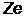( 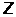–порядковый номер элемента в системе Д.И. Менделеева, е–заряд электрона) под действием сил электростатического притяжения по круговым (или эллиптическим) орбитам движутся электроны (подобно тому, как планеты обращаются вокруг Солнца под действием сил гравитационного притяжения), образуя электронную оболочку атома. Однако, такая модель оказалась несостоятельной. Движение электрона по круговой орбите происходит с нормальным ускорением, поэтому он постоянно излучает электромагнитные волны и теряет свою энергию. В результате через короткое время электрон упадет на ядро и атом перестанет существовать.

Выход из сложившейся ситуации предложил Нильс Бор, который дополнил модель атома Резерфорда двумя постулатами.

Постулаты Бора

Первый постулат Бора (постулат стационарных состояний):

В атоме существуют стационарные (не изменяющиеся со временем) орбиты (состояния), находясь на которых электрон не излучает электромагнитные волны.

Из всех возможных орбит электрона разрешенными являются только те, для которых момент импульса электрона кратен величине 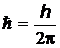, т.е. для которых выполняется условие (правило квантования):

( ),

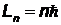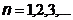где 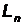–момент импульса электрона на 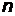- ой орбите, 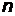- главное квантовое число, 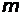–масса электрона, 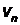–скорость электрона на 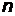–ой орбите радиусом ,

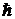= 1,05×10^–34 Дж×с – постоянная Планка. Для круговых орбит, которые рассматриваются в дальнейшем,

Второй постулат Бора (правило частот).

Любое изменение энергии атома связано со скачкообразным переходом из одного стационарного состояния в другое, при этом атом испускает или поглощает фотон, энергия которого определяется выражением (правило частот).

Таким образом, энергия фотона равна модулю разности энергий стационарных состояний электрона до ( ) и после ( ) перехода. Переход из состояния с большей энергией в состояние с меньшей энергией сопровождается излучением фотона. Обратный процесс возможен только при поглощении фотона.

Набор возможных дискретных частот квантовых переходов и определяет линейчатый спектр излучения атома водорода, состоящего из отдельных спектральных линий, расположенных в определенном порядке

Второй закон Ньютона для электрона в водородноподобном ионе имеет вид:

.

Добавив к этому уравнению первый постулат Бора для круговых орбит

,

получим систему из двух уравнений, решая которую, найдем радиусы орбит электронов и их линейные и угловые скорости на орбите с номером n.

Радиусы разрешенных круговых орбит в модели Бора для водородоподобного иона:

,

где – номер орбиты, - электрическая постоянная, 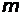- масса электрона, - заряд электрона, 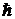- постоянная Планка. Состояние атома с называется основным. Радиус первой орбиты электрона при Z=1 (атом водорода) называется боровским радиусом и обозначается : = 53пм = 5,3×10^–11м. Он является единицей длины в атомной физике. Тогда , т.е. радиусы орбит для стационарных состояний атома водорода равны соответственно

Скорость электрона на орбите с номером в водородоподобном ионе:

м/с,

где м/с – скорость электрона на первой орбите. Приведем выражение для угловой скорости вращения электрона на орбите с номером :

,

где – угловая скорость на первой орбите.

Полная энергия электрона на орбите с номеромn в водородоподобном ионе складывается из его кинетической энергии и потенциальной энергии в электростатическом поле ядра:

Z = 1 соответствует атому водорода. Полная энергия электрона равна

Состояние с номером и энергией эВ – называется основным, остальные значения соответствуют возбужденным состояниям. Для целочисленных , получаем энергетические уровни атома водорода, схематически представленные на Рис.10.

Рис.10 Диаграмма энергетических уровней атома водорода. Показаны переходы, соответствующие различным спектральным сериям.

Полная энергия электрона, являющаяся отрицательной величиной, соответствует ограниченному движению электрона в пространстве по стационарной орбите. Минимальная энергия атома водорода эВ при n = 1.

Переходы электрона с одной орбиты (энергетического уровня) на другую приводят к образованию спектральных серий Лаймана, Бальмера, Пашена, изображенных на Рис.10б. При увеличении номера орбиты n энергия электрона возрастает и при становится равной нулю. Если энергия электрона , то его движение является неограниченным, т.е. он оторвался от ядра атома водорода и произошла ионизация атома. Минимальная энергия, необходимая для удаления электрона из атома (водородоподобного иона) называется энергией ионизации :

Дж= 13,6 эВ.

Энергия возбуждения – минимальная энергия, которую необходимо сообщить атому водорода (водородоподобному иону), чтобы электрон из основного состояния перешел в возбужденное.

Энергия связи данного состояния – энергия, необходимая для удаления электрона из атома (водородоподобного иона), находящегося в данном возбужденном состоянии.

Потенциалом ионизации называется ускоряющая разность потенциалов, которую должен пройти бомбардирующий электрон, чтобы приобрести энергию, достаточную для ионизации атома (водородоподобного иона): В. Энергия ионизации, выраженная в электронвольтах, численно равна потенциалу ионизации.

Первый потенциал возбуждения U₁ есть наименьшая разность потенциалов, которую должен пройти в ускоряющем поле электрон, чтобы при столкновении с невозбужденным атомом водорода (водородоподобным ионом) перевести его в первое возбужденное состояние:

, так как =1 и =2. =10,2Z² В. Для атома водорода (Z=1) U₁=10,2В