Определение прогиба и угла поворота с помощью интеграла Мора с использованием правила Верещагина

Для определения прогиба балки в сечении 1, выбираем единичное состояние – освободив балку от заданной нагрузки, прикладываем в сечении 1 сосредоточенную силу 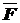=1, направленную вертикально вниз (рис.26г).

Рис.26. Грузовая эпюра и эпюры от единичных силовых факторов

Определение опорных реакций.

Промежуточный шарнир позволяет составить дополнительное уравнение – сумма моментов всех сил, расположенных слева (справа) от шарнира равна нулю: R_D=0.

Остальные уравнения статики составляются для всей балки:

S F_x =0: H_A= 0.

S M_A =0: ;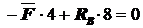

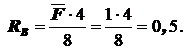
S M_B=0: 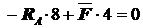; R_A = .

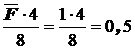Проверка S F_z =0? .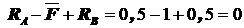

Значения изгибающих моментов.

Участок AE: ;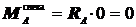

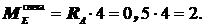
Участок BE: ;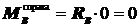

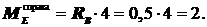
Строим эпюру 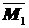от единичного воздействия (рис.26д). Прогиб балки в сечении 1 (v₁) вычислим с помощью интеграла Мора

v₁=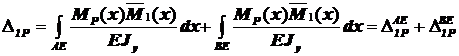

Эпюру от заданной нагрузки М_Р на участке AE разбиваем на две простейшие эпюры ( 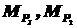) – треугольник и симметричную параболу (рис.27).

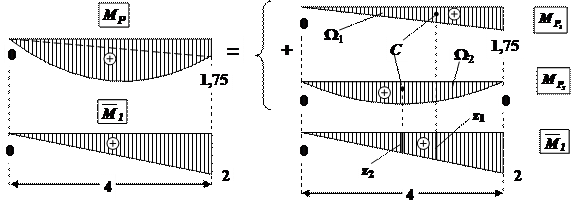
Рис.27. Разбиение сложной эпюры на простые эпюры. Перемножение эпюр

Площади этих эпюр: ; .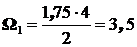

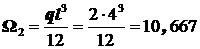Ординаты в эпюре 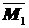под центрами тяжести соответственно равны 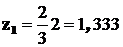; 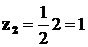, поэтому

.

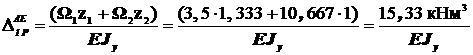Эпюру М_Р на участке BE разбиваем на два треугольника (рис.28).

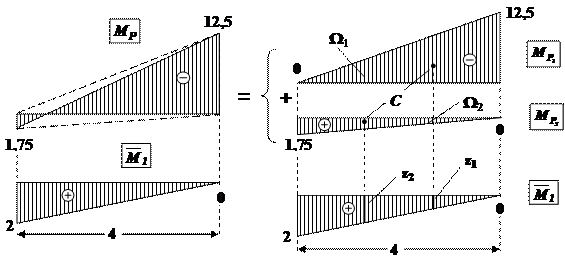Рис.28. Разбиение сложной эпюры на простые эпюры. Перемножение эпюр

Площади этих эпюр: ; .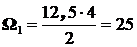

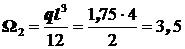Ординаты в эпюре 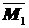под центрами тяжести соответственно равны 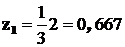; 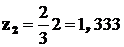, поэтому

.

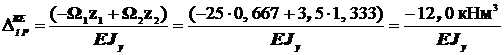Таким образом, прогиб в сечении 1 будет равен

v₁=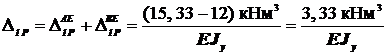

Положительное значение прогиба показывает, что балка в сечении 1 перемещается вниз в направлении единичной силы.

Определение угла поворота в сечение 2

Сечение 2 совпадает с шарниром, поэтому будем определять взаимный угол поворота примыкающих к шарниру сечений. Выбираем единичное состояние – освободив балку от заданной нагрузки, прикладываем в сечение 2(сечение C) единичные сосредоточенные моменты ( 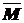=1) слева и справа от шарнира, как показано на рис.26е .

Определение опорных реакций.

Используя промежуточный шарнир, составляем дополнительное уравнение: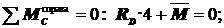

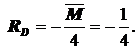
Остальные уравнения статики составляются для всей балки:

S F_x =0: H_A= 0.

S M_A =0: R_B·8+ R_D·14=0;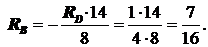

S M_B=0: –R_A ·8+ R_D ·6=0; R_A = .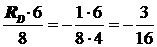

Проверка S F_z =0? R_A + R_B+R_C =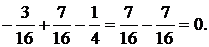

Значения изгибающих моментов.

Участок AB: ;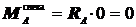

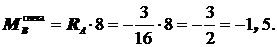
Участок BC: ;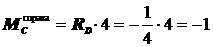

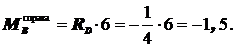
Участок CD: ;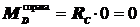

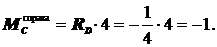
Строим эпюру 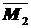от единичного воздействия (рис.26ж).

Взаимный угол поворота в сечении 2 вычислим с помощью интеграла Мора

∆j₂ =∆_2P = .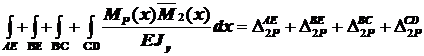

Эпюру М_Р на участке AE разбиваем на – треугольник и симметричную параболу (рис.29).

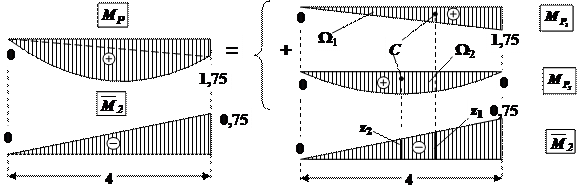
Рис.29. Разбиение сложной эпюры на простые эпюры. Перемножение эпюр

Площади этих эпюр: ; .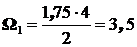

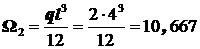Ординаты в эпюре 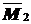под центрами тяжести соответственно равны 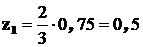; ; 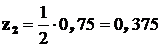поэтому

.

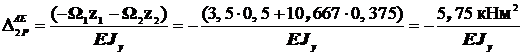Эпюру от заданной нагрузки М_Р на участке BE разбиваем на два треугольника, эпюру от единичного момента также на два треугольника (рис.30).

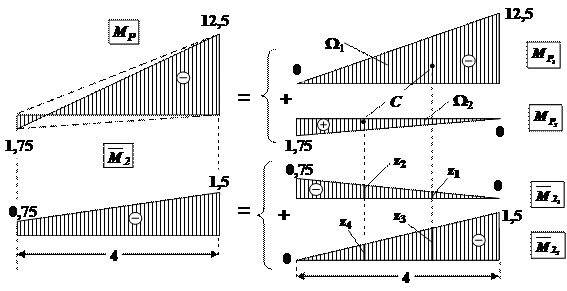
Рис.30. Разбиение сложных эпюр на простые эпюры. Перемножение эпюр

Площади этих эпюр: ; .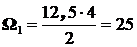

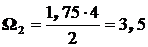Ординаты в эпюре 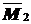под центрами тяжести соответственно равны 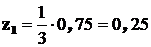; ; 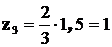; ; 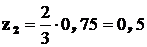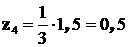поэтому

.

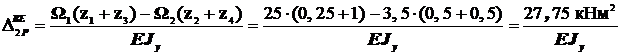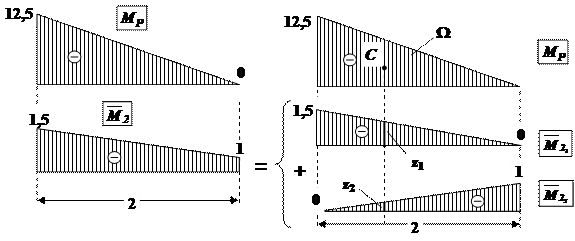На участке BC эпюру от единичного момента разбиваем на два треугольника (рис.31).

Рис.31. Разбиение сложной эпюры на простые эпюры. Перемножение эпюр

Площадь эпюры: .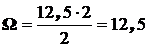

Ординаты в эпюре 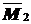под центром тяжести соответственно равны: 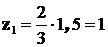; ; ; 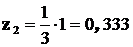поэтому

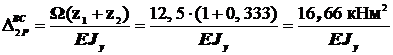
На участке CD (рис.25) площадь эпюры: .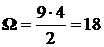

Ордината в эпюре 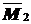под центром тяжести равна: 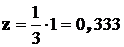; поэтому .

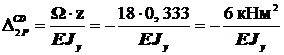Взаимный угол поворота в сечении 2

∆j₂ =∆_2P = .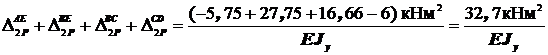

Положительное значение угла поворота показывает, что сечения слева и справа от шарнира С поворачиваются по направлению единичных моментов.