Вынужденные электромагнитные колебания в замкнутом контуре.
Вынужденные электромагнитные колебания в замкнутом контуре.
Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическимии вынужденными электромагнитными колебаниями.
Уравнения 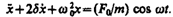 и
и 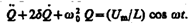 можно свести к линейному неоднородному дифференциальному уравнению
можно свести к линейному неоднородному дифференциальному уравнению
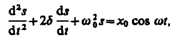 (147.5)
(147.5)
применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (x0 в случае механических колебаний равно F0/m, в случае электромагнитных — Um/L).
Уравнение бегущей волны.
Бегущими волнами называютсяволны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуетсявектором плотности потока энергии. Этот вектор для упругих вол называется вектором Умова [по имени русского ученого Н. А. Умова (1846 — 1915), решившего задачу о распространении энергии в среде]. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны.
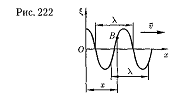
В данном случае волновые поверхности перпендикулярны
оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение 6, будет зависеть только от х и t,т.е.Е=Е,(х,t). На рисунке рассмотрим некоторую частицу В среды, находящуюся от источника колебаний О на расстоянии х.Если колебания точек, лежащих в плоскости х = 0,описываются функцией Е(0,t) = A coswt), то частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на т, так как для прохождения волной расстояния х требуется время т = х/v, где v — скоростьраспространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид 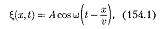 откуда следует, что E(x:t) является не
откуда следует, что E(x:t) является не
только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны.
Построение изображений в тонких линзах. Призма
Расчет.
 Расчет интерференционной картины можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу.
Расчет интерференционной картины можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу.
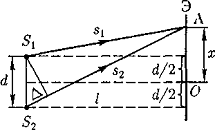
Щели S1 и S2 находятся на расстоянии d друг от друга и являются когерентными (реальными или мнимыми изображениями источника S в какой-то оптической системе) источниками света. Интерференция наблюдается в произвольной точке А экрана, параллельного обеим щелям и расположенного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей. Интенсивность в любой точке А экрана, лежащей на расстоянии х от О, определяется оптической разностью хода D=s2—s1 (см. § 172). Из рис. имеем
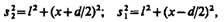 откуда
откуда 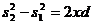 , или
, или 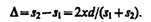
Из условия l >> d следует, что s1 + s2 » 2l, поэтому 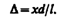
Подставив найденное значение D (173.1) в условия (172.2) и (172.3), получим, что максимумы интенсивности будут наблюдаться в случае, если
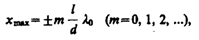 а минимумы — в случае, если
а минимумы — в случае, если 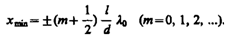 (173.3)
(173.3)
Расстояние между двумя соседними максимумами (или минимумами), называемое шириной интерференционной полосы, равно 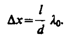 (173.4)
(173.4)
Dx не зависит от порядка интерференции (величины т) и является постоянной для данных l, d и l0.
Из выражений (173.2) и (173.3) следует, таким образом, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос, параллельных друг другу.
ГИПОТЕЗА ДЕ БРОЙЛЯ
Де Бройль выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.
Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия Е и импульс p, а с другой — волновые характеристики — частота n и длина волны l. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов: 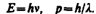 Смелость гипотезы де Бройля заключалась именно в том, что соотношение (213.1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемойпо формуле де Бройля:
Смелость гипотезы де Бройля заключалась именно в том, что соотношение (213.1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемойпо формуле де Бройля: 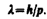 Это соотношение справедливо для любой частицы с импульсом р.
Это соотношение справедливо для любой частицы с импульсом р.
Вскоре гипотеза де Бройля была подтверждена экспериментально. В 1927 г. американские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кристалла никеля, — дает отчетливую дифракционную картину. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов (182.1), а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (213.2). В дальнейшем формула де Бройля была подтверждена опытами П. С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (энергия »50 кэВ) через металлическую фольгу (толщиной »1 мкм).
Так как дифракционная картина исследовалась для потока электронов, то необходимо было доказать, что волновые свойства присущи не только потоку большой совокупности электронов, но и каждому электрону в отдельности. Это удалось экспериментально подтвердить в 1948 г. российскому физику В. А. Фабриканту (р. 1907). Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других (промежуток времени между двумя электронами в 104 раз больше времени прохождения электроном прибора), возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частице в отдельности.
Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля (213.2). Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких,как электронография и нейтронография (см. § 182), а также к возникновению новой отрасли науки — электронной оптики (см. § 169).
Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что перед нами универсальное явление, общее свойство материи. Но тогда волновые свойства должны быть присущи и макроскопическим телам. Почему же они не обнаружены экспериментально? Например, частице массой 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с l = 6,62×10–31 м. Такая длина волны лежит за пределами доступной наблюдению области (периодических структур с периодом d»10–31 м не существует). Поэтому считается, что макроскопические тела проявляют только одну сторону своих свойств — корпускулярную — и не проявляют волновую.
Представление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы e и частотой n волн де Бройля: 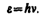 (213.3)
(213.3)
Это свидетельствует о том, что соотношение между энергией и частотой в формуле (213.3) имеет характер универсального соотношения, справедливогокак для фотонов, так и для любых других микрочастиц. Справедливость же соотношения (213.3) вытекает из согласия с опытом тех теоретических результатов, которые получены с его помощью в квантовой механике, атомной и ядерной физике.
Подтвержденная экспериментально гипотеза да Бройля о корпускулярно-волновом дуализме свойств вещества коренным образом изменила представления о свойствах микрообъектов. Всем микрообъектам присущи и корпускулярные, и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в классическом понимании. Современная трактовка корпускулярно-волнового дуализма может быть выражена словами академика В. А. Фока (1898—1974): «Можно сказать, что для атомного объекта существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна—частица. Всякое иное, более буквальное, понимание этого дуализма в вида какой-нибудь модели неправильно.» (в сб.: Философские вопросы современной физики. — М.: Изд-во АН СССР, 1959).
46. РАДИОАКТИВНОЕ ИЗЛУЧЕНИЕ И ЕГО ВИДЫ
Французский физик А. Беккерель (1852—1908) в 1896 г. при изучении люминесценции солей урана случайно обнаружил самопроизвольное испускание ими излучения неизвестной природы, которое действовало на фотопластинку, ионизировало воздух, проникало сквозь тонкие металлические пластинки, вызывало люминесценцию ряда веществ. Продолжая исследование этого явления, супруги Кюри — Мария (1867—1934) и Пьер — обнаружили, что беккерелевское излучение свойственно не только урану, но и многим другим тяжелым элементам, таким, как торий и актиний. Они показали также, что урановая смоляная обманка (руда, из которой добывается металлический уран) испускает излучение, интенсивность которого во много раз превышает интенсивность излучения урана. Таким образом удалось выделить два новых элемента — носителя беккерелевского излучения: полоний 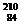 Рo и радий
Рo и радий 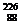 Ra.
Ra.
Обнаруженное излучение было названорадиоактивным излучением, а само явление — испускание радиоактивного излучения —радиоактивностью.
Дальнейшие опыты показали, что на характер радиоактивного излучения препарата не оказывают влияния вид химического соединения, агрегатное состояние, механическое давление, температура, электрические и магнитные поля, т. е. все те воздействия, которые могли бы привести к изменению состояния электронной оболочки атома. Следовательно, радиоактивные свойства элемента обусловлены лишь структурой его ядра.
В настоящее время подрадиоактивностью понимают способность некоторых атомных ядер самопроизвольно (спонтанно) превращаться в другие ядра с испусканием различных видов радиоактивных излучений и элементарных частиц. Радиоактивность подразделяется наестественную (наблюдается у неустойчивых изотопов, существующих в природе) иискусственную (наблюдается у изотопов, полученных посредством ядерных реакций). Принципиального различия между этими двумя типами радиоактивности нет, так как законы радиоактивного превращения в обоих случаях одинаковы.
Радиоактивное излучение бывает трех типов: a-, b- и g-излучение. Подробное их исследование позволило выяснить природу и основные свойства.
a-Излучение отклоняется электрическим и магнитным полями, обладает высокой ионизирующей способностью и малой проникающей способностью (например, поглощаются слоем алюминия толщиной примерно 0,05 мм). a-Излучение представляет собой поток ядер гелия; заряд a-частицы равен +2е, а масса совпадает с массой ядра изотопа гелия 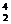 Не. По отклонению a-частиц в электрическом и магнитном полях был определен их удельный заряд Q/ma , значение которого подтвердило правильность представлений об их природе.
Не. По отклонению a-частиц в электрическом и магнитном полях был определен их удельный заряд Q/ma , значение которого подтвердило правильность представлений об их природе.
b-Излучение отклоняется электрическим и магнитным полями; его ионизирующая способность значительно меньше (примерно на два порядка), а проникающая способность гораздо больше (поглощается слоем алюминия толщиной примерно 2 мм), чем у a-частиц. b-Излучение представляет собой поток быстрых электронов (это вытекает из определения их удельного заряда).
g-Излучение не отклоняется электрическим и магнитным полями, обладает относительно слабой ионизирующей способностью и очень большой проникающей способностью (например, проходит через слой свинца толщиной 5 см), при прохождении через кристаллы обнаруживает дифракцию. g-Излучение представляет собой коротковолновое электромагнитное излучение с чрезвычайно малой длиной волны l<10–10 м и вследствие этого — ярко выраженными корпускулярными свойствами, т.е. является потоком частиц — g-квантов (фотонов).
47. ДЕФЕКТ МАССЫ И ЭНЕРГИЯ СВЯЗИ ЯДРА
Исследования показывают, что атомные ядра являются устойчивыми образованиями. Это означает, что в ядре между нуклонами существует определенная связь.
Массу ядер очень точно можно определить с помощью масс-спектрометров — измерительных приборов, разделяющих с помощью электрических и магнитных полей пучки заряженных частиц (обычно ионов) с разными удельными зарядами Q/m. Масс-спектрометрические измерения показали, что масса ядра меньше, чем сумма масс составляющих его нуклонов. Но так как всякому изменению массы должно соответствовать изменение энергии, то, следовательно, при образовании ядра должна выделяться определенная энергия. Из закона сохранения энергии вытекает и обратное: для разделения ядра на составные части необходимо затратить такое же количество энергии, которое выделяется при его образовании. Энергия, которую необходимо затратить, чтобы расщепить ядро на отдельные нуклоны, называетсяэнергией связи ядра.
Согласно выражению, энергия связи нуклонов в ядре
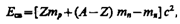
где тp, тn, тя — соответственно массы протона, нейтрона и ядра. В таблицах обычно приводятся не массы тя ядер, а массы т атомов. Поэтому для энергии связи ядра пользуются формулой
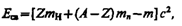 (252.2)
(252.2)
где mH — масса атома водорода. Так как mH больше mp на величину me, то первый член в квадратных скобках включает в себя массу Z электронов. Но так как масса атома т отличается от массы ядра тя как раз на массу Z электронов, то вычисления по формулам (252.1) и (252.2) приводят к одинаковым результатам.
Величина
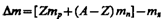
называетсядефектом массы ядра. На эту величину уменьшается масса всех нуклонов при образовании из них атомного ядра.
Часто вместо энергии связи рассматривают удельную энергию связи dEсв — энергию связи, отнесенную к одному нуклону. Она характеризует устойчивость (прочность) атомных ядер, т. е. чем больше dEсв, тем устойчивее ядро. Удельная энергия связи зависит от массового числа А элемента. Для легких ядер (А£12) удельная энергия связи круто возрастает до 6¸7 МэВ, претерпевая целый ряд, затем более медленно возрастает до максимальной величины 8,7 МэВ у элементов с А=50¸60, а потом постепенно уменьшается у тяжелых элементов (например, для 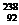 U она составляет 7,6 МэВ).
U она составляет 7,6 МэВ).
Уменьшение удельной энергии связи при переходе к тяжелым элементам объясняется тем, что с возрастанием числа протонов в ядре увеличивается и энергия их кулоновского отталкивания. Поэтому связь между нуклонами становится менее сильной, а сами ядра менее прочными.
Наиболее устойчивыми оказываются так называемыемагические ядра, у которых число протонов или число нейтронов равно одному из магических чисел: 2, 8, 20, 28, 50, 82, 126. Особенно стабильныдважды магические ядра, у которых магическими являются и число протонов, и число нейтронов (этих ядер насчитывается всего пять: 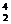 Не,
Не, 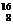 O,
O, 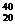 Ca,
Ca, 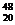 Ca,
Ca, 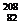 Pb).
Pb).
Следует, что наиболее устойчивыми с энергетической точки зрения являются ядра средней части таблицы Менделеева. Тяжелые и легкие ядра менее устойчивы. Это означает, что энергетически выгодны следующие процессы: 1) деление тяжелых ядер на более легкие; 2) слияние легких ядер друг с другом в более тяжелые. При обоих процессах выделяется огромное количество энергии; эти процессы в настоящее время осуществлены практически: реакции деления и термоядерные реакции.
Чернобыльская катастрофа
Авария на Чернобыльской АЭС, Катастрофа на Чернобыльской АЭС, Черно́быльская авария — разрушение 26 апреля 1986 годачетвёртого энергоблока Чернобыльской атомной электростанции, расположенной на территории Украинской ССР (ныне — Украина). Разрушение носило взрывной характер, реактор был полностью разрушен, и в окружающую среду было выброшено большое количестворадиоактивных веществ. Авария расценивается как крупнейшая в своём роде за всю историю атомной энергетики, как по предполагаемому количеству погибших и пострадавших от её последствий людей, так и по экономическому ущербу. В течение первых трех месяцев после аварии погиб 31 человек; отдалённые последствия облучения, выявленные за последующие 15 лет, стали причиной гибели от 60 до 80 человек[1][2]. 134 человека перенесли лучевую болезнь той или иной степени тяжести, более 115 тыс. человек из 30-километровой зоны были эвакуированы[2]. Для ликвидации последствий были мобилизованы значительные ресурсы, более 600 тыс. человек участвовали в ликвидации последствий аварии[3].
В отличие от бомбардировок Хиросимы и Нагасаки, взрыв напоминал очень мощную «грязную бомбу» — основным поражающим факторомстало радиоактивное заражение.
Облако, образовавшееся от горящего реактора, разнесло различные радиоактивные материалы, и прежде всего радионуклиды йода и цезия, по большей части территории Европы. Наибольшие выпадения отмечались на значительных территориях в Советском Союзе, расположенных вблизи реактора и относящихся теперь к территориям Белоруссии, Российской Федерации и Украины[4].
Чернобыльская авария стала событием большого общественно-политического значения для СССР, её ликвидация обошлась Советскому Союзу в сумму, близкую к 25 миллиардам долларов.[источник не указан 62 дня] Всё это наложило определённый отпечаток на ход расследования её причин[5]. Подход к интерпретации фактов и обстоятельств аварии менялся с течением времени, и полностью единого мнения нет до сих пор.
Основными факторами, внесшими вклад в возникновение аварии
· реактор не соответствовал нормам безопасности и имел опасные конструктивные особенности;
· низкое качество регламента эксплуатации в части обеспечения безопасности;
· неэффективность режима регулирования и надзора за безопасностью в ядерной энергетике, общая недостаточность культуры безопасности в ядерных вопросах как на национальном, так и на местном уровне;
· отсутствовал эффективный обмен информацией по безопасности как между операторами, так и между операторами и проектировщиками, персонал не обладал достаточным пониманием особенностей станции, влияющих на безопасность;
· персонал допустил ряд ошибок и нарушил существующие инструкции и программу испытаний.
Вынужденные электромагнитные колебания в замкнутом контуре.
Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическимии вынужденными электромагнитными колебаниями.
Уравнения 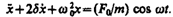 и
и 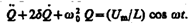 можно свести к линейному неоднородному дифференциальному уравнению
можно свести к линейному неоднородному дифференциальному уравнению
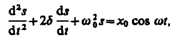 (147.5)
(147.5)
применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (x0 в случае механических колебаний равно F0/m, в случае электромагнитных — Um/L).
Уравнение бегущей волны.
Бегущими волнами называютсяволны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуетсявектором плотности потока энергии. Этот вектор для упругих вол называется вектором Умова [по имени русского ученого Н. А. Умова (1846 — 1915), решившего задачу о распространении энергии в среде]. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны.

В данном случае волновые поверхности перпендикулярны
оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение 6, будет зависеть только от х и t,т.е.Е=Е,(х,t). На рисунке рассмотрим некоторую частицу В среды, находящуюся от источника колебаний О на расстоянии х.Если колебания точек, лежащих в плоскости х = 0,описываются функцией Е(0,t) = A coswt), то частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на т, так как для прохождения волной расстояния х требуется время т = х/v, где v — скоростьраспространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид 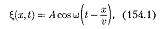 откуда следует, что E(x:t) является не
откуда следует, что E(x:t) является не
только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны.
