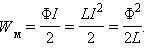Электромагнитная индукция. Э.Д.С. индукции. Самоиндукция. Энергия магнитного поля.

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.

Величина ЭДС индукции в контуре определяется выражением

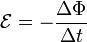
где 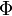— поток магнитного поля через замкнутую поверхность 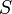, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре

Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре при изменении тока, протекающего по контуру.

.

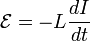энергия W_м магнитного поля катушки с индуктивностью L, создаваемого током I, равна

2.7 Колебательный контур. Электромагнитные колебания. Период электромагнитных колебаний( Формула Томсона). Открытый колебательный контур(антенна).

Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор.

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Периодические изменения во времени электрического заряда (силы тока, напряжения) называются электромагнитными колебаниями.

ЭМ колебания: энергия заряженного конденсатора постепенно превращается в энергию магнитного поля катушки, и наоборот.

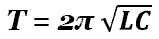- формула Томсона, формула периода электромагнитных колебаний в колебательном контуре.

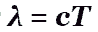- длина электромагнитной волны и период колебаний.
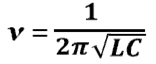- частота электромагнитных колебаний.

. Если контур состоит из катушки и двух пластин плоского конденсатора, не параллельных друг другу, то чем под большим углом развернуты эти пластины. тем более свободно выходит электромагнитное поле в окружающее пространство .Предельным случаем раскрытия к0олебательного контура является удаление пластин конденсатора на противоположные концы прямой катушки. Такая система называется открытым колебательным контуром . Изображение пластин конденсатора на концах катушки открытого колебательного контура является лишь условностью. В действительности контур состоит из катушки и длинного провода — антенны. Один конец антенны заземлен, второй поднят над. поверхностью земли

2.8 Основные положения теории электромагнитного поля Максвелла. Возникновение (образование) электромагнитной волны.

Основные положения теории Максвелла

1,Переменное магнитное поле порождает в окружающем пространстве

вихревое электрическое поле.

2. Переменное электрическое поле порождает в окружающем пространстве

магнитное поле.

3. Силовые линии магнитного поля всегда замкнуты.

4. Электрическое поле с незамкнутыми линиями порождается электрическими зарядами.

Электромагнитное поле в каждой точке пространства характеризуется напряженностью Е и индукцией В. Возникновение электромагнитной волны можно представить так: в некоторой области пространства возникают колебания электрического заряда, например между контактами электрической цепи проскакивает искра. Это повлечет за собой колебания вектора напряженности Е, т. е. его модуль и направление станут периодически меняться. Согласно теории Максвелла, в этой же области будут происходить колебания вектора магнитной индукции Б. Эти колебания порождают электромагнитные волны, распространяющиеся в пространстве.
Теория Максвелла показала, что электромагнитные волны — волны поперечные, их скорость распространения в вакууме примерно равна 300 000 км/с, эта волна несет энергию.

Колебания и волны.

Механические колебания. Смещение, период, частота, амплитуда фаза и циклическая частота колебаний. Гармонические колебания. Уравнение гармонических колебаний. Скорость и ускорение движения при гармонических колебаниях. Связь ускорения со смещением.

Механические колебания – это движение тела, в ходе которого оно многократно движется по одной и той же траектории и проходит при этом одни и те же точки пространства. Физическая величина, которая изменяется со временем при колебательном движении, называется смещением.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний T — это время одного полного колебания. Можно сказать, что за период

тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: 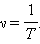Частота измеряется в

герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Фаза является свойством колебательного движения, которое характеризует величину смещения тела в любой момент времени. Измеряется фаза в радианах.

Циклическая частота ω = 2πν. Она связана с периодом отношением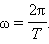

Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса. x=x₀cos(ω₀t + φ₀)

Скорость v_x=-Aωsin(ω₀t + φ₀)

Ускорениеa_x=Aω²cos(ω₀t + φ₀)

Связь ускорения со смещением: a_x=- ω²x

Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.

Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы

Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание)

Частота — число колебаний в единицу времени

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота 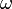(рад/сек, Гц, сек⁻¹), показывающая число колебаний за единиц времени:

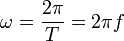
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

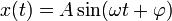
или

,

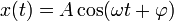где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, 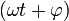— полная фаза колебаний, 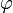— начальная фаза колебаний.

Согласно определению скорости, скорость – это производная от координаты по времени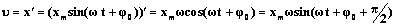

Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на p/2.

Величина 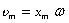- максимальная скорость колебательного движения (амплитуда колебаний скорости).

Согласно определению ускорения, ускорение – это производная от скорости по времени:

-

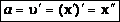вторая производная от координаты по времени. Тогда: .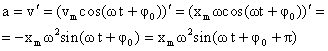

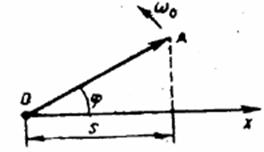
Гармонические колебания изображаются графически методом вращающегося вектора

амплитуды, или методом векторных диаграмм.

Для этого из произвольной точки О, выбранной на оси x под углом j,

равным начальной фазе колебания, откладывается вектор А, модуль которого равен

амплитуде А рассматриваемого колебания

Если этот вектор привести во вращение с угловой скоростью w0, равной циклическойчастоте колебаний, то проекция конца вектора будет перемещаться по оси x и принимать значения от -А до +А , а колеблющаяся величина будетизменяться со временем по закону s =A cos (w0 t +j). Таким образом,гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольнойточки оси под углом j, равным начальной фазе, и вращающегося с угловойскоростью w0 вокруг этой точки.

Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на p/2 и колебания смещения на p (говорят, что колебания происходят в противофазе).

Величина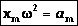

- максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: ,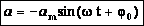

а для случая нулевой начальной фазы: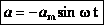

Сравним выражения для смещения и ускорения при гармонических колебаниях:

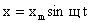и .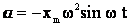

Можно записать: -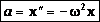

т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.

Представление гармонических колебаний в виде вращающегося вектора. Сложение двух гармонических колебаний с одинаковыми частотами, совершающихся в одном направлении. Условия усиления и максимального усиления колебаний.