Вычисление моментов инерции тел правильной формы.

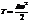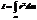Пусть нам дан стержень, поперечное сечение которого S , плотность ρ, длина l.Необходимо определить момент инерции стержня через торец стержня.

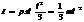Его элементарная масса dm= 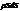. Момент инерции dI= 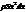, - момент инерции стержня относит оси, проход через его торец.

Момент инерц. цилиндра и обруча относит оси, проход через центр. 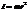. Мом. ин стержня относ. оси, проход через середину стержня мом. инерции шара, относит оси, проход через его центр.

19)Полная кинетическая энергия катящегося тела. Закон сохранения момента импульса.

Полная кинетическая энергия катящегося тела – Колесо вращается, при этом участвует в двух движениях. Центр тяжести движется поступательно, со скоростью υ_л, с другой стороны вращаются все точки относительно центр. Оси. Вращаются с угловой скоростью ω, при этом ось перемещ. Со скор.υ то кинетическая энергия T вращ-ся ц-ра или колеса

T=Iω²/2+mυ²/2

Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени: 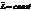. Это фундаментальный закон природы. Он является следствием изотропности пространства : инвариантность физических законов относительно выбора направления осей координат системы отсчёта.

Момент импульса твёрдого тела относительно оси есть сумма моментов импульса отдельных частиц:

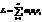
Учитывая, что 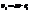, получим:

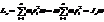Продифференцируем это р-ние по времени:

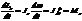Можно показать, что имеет место векторное рав-во: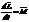

Это выражение – ещё одна форма уравнения динамики вращательного движения твёрдого тела относительно неподвижной оси: производная момента импульса твёрдого тел относительно оси равна моменту сил относительно той же оси.

В замкнутой системе момент внешних сил М=0 и 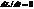откуда L=cons

20)Основное уравнение динамики вращательного движения твёрдого тела.

M¯=dL¯/dt Момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно той-же оси на угловое ускорение M=Iε

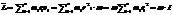Рассмотрим момент кол-ва движения отдельной частицы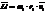

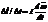
V= 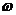* 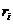Линейная скорость

22)Механический принцип относительности. Преобразования Галилея.

Механический принцип относительности:законы динамики одинаковы во всех инерциальных системах отсчёта. Система К’ движется равномерно и прямолинейно со скоростью u (u-const) Скорость направлена вдоль ОО” , тогда вектор перемещения равен произведению скорости на время.

В основе механики лежат преобразования Галилея.

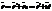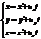Преобразования координат Галилея: Задают связь между радиусами-векторами или координатами произвольной точки А в обеих системах: или .Время в системах протекает одинаково.

Основы классической физики в следующих 5-и постулатах:

1. Принцип относительности Галилея.

2. Утверждение о принципиальной возможности бесконеч скорости передачи взаимодействий.

3. Предположение о неограниченности, относительности скорости в инерциальных с.о.

4. Это предположение о Евклидовости, трёхмерности, непрерывности, однородности, изотропности и односвязности пространства в инерциальных с.о.

5. Предположение об однородности, одномерности, непрерывности, однонаправленности вр. В инерц с.о.

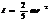23)Постулаты специальной теории относительности. Преобразования Лоренца и их следствия.

Специальная теория относительности:специальная теория относительности основывается на двух постулатах Эйнштейна:

1. Все законы природы инвариантны при переходе от одной инерциальной с.о. к другой.

2. Скорость распространения света в вакууме не зависит от относительных скоростей и это означает существования конечной скорости распространения взаимодействий.

Преобразования Лоренца (при 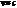): Система K’ движется относительно системы К со скоростью

v=const.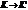

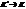
Преобразования Лоренца имеют следующий вид: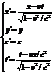

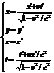
1. Эти ур-ния симметричны и отличаются лишь знаком при v, что очевидно.

2. При v<<c они переходят в классические преобразования Галилея.

В закон преобразования координат входит время, а в закон преобразования времени – пространственные координаты (устанавливается взаимосвязь пространства и времени).

24)Релятивистская масса и импульс. Понятие одновременности, относительность длин и промежутков времени.

Релятивистский импульс:

Закон сохранения релятивистского импульса: реалятив импульс замк системы сохр, т.е. не изм с теч времени. (следствие однородности пространства)

Основной закон релятивистской динамики:

Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной с.о. к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца.

Релятивистское выражение для кинетической энергии:

Поскольку полная энергия в релятивистской динамике – это сумма кинетической энергии и энергии покоя, т.к. энергия покоя равна : 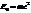и полная энергия равна :

где m – масса частицы, v – её скорость, то окончательно мы имеем:

Понятие одновременности. Относительность длин и промежутков времени:

Относительность одновременности: Пусть системе К в точках х1 и х2 в моменты времени t1 и t2 происходят два события. В системе K’ им соответствуют координаты x1’ и x2’ и моменты времени t1’ и t2’. Если события в системе К происходят в одной точке (х1=х2) и являются одновременными (t1=t2), то, согласно преобразованиям Лоренца,

x1’=x2’, t1’=t2’,

Т.е. эти события в системе К явл одновременными и пространственно совпадающими для любой инерциальной системы отсчёта.

Если события в системе К разобщены (х1<>х2), но одновременны, то в системе K’, согласно преобразованиям Лоренца,

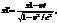
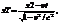
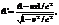
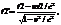Т.е.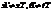

Таким образом, в системе K’ эти события, оставаясь пространственно разобщёнными, оказываются и неодновременными.

Длительность событий в разных с.о.:Пусть в некоторой точке (с координатой х), покоящейся относительно системы К, происходит событие, длительность которого T=t1-t2, где 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе K’: T’=t2’-t1’ (*) , где

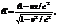
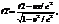Подставив в (*), получаем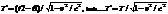

T<T’, т.е. длительность события, происходящего в некоторой точке наименьшая в той инерциальной с.о., относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной с.о., идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчёта, относительно которой часы движутся.

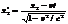Относительность длин-Пусть в движ. сист. отсчета вдоль отн. k длинной 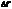= 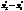, где х1-коор нач отр, x2-коор конца отр

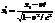отсюда =

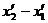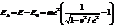
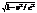видно, что 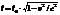Таким образом наблюдатель видит,что длина движ. отрезка в раз меньше собств. длины, измеренной в сист., где этот отрезок покоится.