Импульс. Законы сохранения импульса

Импульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости:
Закон сохранения импульса утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.. , при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
находят применение при создании современной ракетно-космической техники. Движение с помощью реактивной струи по закону сохранения импульса лежит в основе гидрореактивного двигателя. В основе движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатиц) также лежит реактивный принцип.

Работа силы . Мощность . КПД.

работа силы
Понятие “работа“ как физическая величина во всех энциклопедиях, справочниках и учебниках раскрывается как понятие “работа силы“ при описании прямолинейной механической формы движения.
Работа силы - мера механического действия силы при перемещении точки ее приложения.
Работа силы есть скалярная физическая величина, равная произведению:
- силы;
- перемещения; и
- косинуса угла между направлением действия силы и перемещением.

РАБОТА силы - мера действия силы, зависящая от численной величины и направления силы F и от перемещения s точки ее приложения.

Мощность. КПд

Любая машина, которая используется для выполнения работы, характеризуется особой величиной, которая называется мощностью.

Мощность - это физическая величина, равная отношению работы ко времени, за который эта работа была выполнена. Мощность обозначается буквой N и в Системе Интернациональной измеряется в ваттах, в честь английского ученого 18-19 века Джеймса Уатта. Если мощность известна, то работу, которая выполняется за единицу времени, можно найти как произведение мощности на время. Поэтому за единицу работы можно взять работу, которая выполняется за 1 секунду при мощности 1 ватт. Такая единица работы называется ватт-секундой (Вт • с).

Если тело движется равномерно, то его мощность можно рассчитать как произведение силы тяги и скорости движения.

В реальных условиях часть механической энергии всегда теряется, поскольку идет на увеличение внутренней энергии двигателя и других частей машины. Для того чтобы характеризовать эффективность двигателей и устройств, пользуются коэффициентом полезного действия.

Коэффициент полезного действия (КПД) - это физическая величина, равная отношению полезной работы к полной работы. КПД обозначается буквой η и измеряется в процентах. Полезная работа всегда меньше полной. КПД всегда меньше 100%.

Кинетическая инергия. Теорема Кенинга.

Теоре́ма Кёнига позволяет выразить полную кинетическую энергию механической системы через энергию движения центра масс и энергию движения относительно центра масс.

Формулировка

Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

где 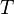— полная кинетическая энергия системы, — кинетическая энергия движения центра масс, — относительная кинетическая энергия системы^[2].

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её сферическом движении относительно центра масс.

Вывод

Приведём доказательство теоремы Кёнига для случая, когда массы тел, образующих механическую систему 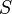, распределены непрерывно^[3].

Найдём относительную кинетическую энергию системы 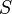, трактуя её как кинетическую энергию, вычисленную относительно подвижной системы координат. Пусть — радиус-вектор рассматриваемой точки системы 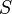в подвижной системе координат. Тогда^[4]:

где точкой обозначено скалярное произведение, а интегрирование ведётся по области пространства, занимаемой системой в текущий момент времени.

Если — радиус-вектор начала координат подвижной системы, а — радиус-вектор рассматриваемой точки системы 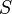в исходной системе координат, то верно соотношение:

Вычислим полную кинетическую энергию системы в случае, когда начало координат подвижной системы помещено в её центр масс. С учётом предыдущего соотношения имеем:

Учитывая, что радиус-вектор одинаков для всех , можно, раскрыв скобки, вынести за знак интеграла:

Первое слагаемое в правой части этой формулы (совпадающее с кинетической энергией материальной точки, которая помещена в начало координат подвижной системы и имеет массу, равную массе механической системы) может интерпретироваться^[2] как кинетическая энергия движения центра масс.

Второе слагаемое равно нулю, поскольку второй сомножитель в нём получается дифференцированием по времени произведения радиус-вектора центра масс на массу системы^[5], но упомянутый радиус-вектор (а с ним и всё произведение) равен нулю:

так как начало координат подвижной системы находится (по сделанному предположению) в центре масс.

Третье же слагаемое, как было уже показано, равно , т. е. относительной кинетической энергии системы .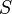

инетическую энергию материальной точки массой m, движущейся с абсолютной скоростью , определяют по формуле

где

Кинетическая энергия механической системы равна сумме кинетических энергий всех точек этой системы

Потенциальная инергия

Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении^[1]. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[2]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными (потенциальными).

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Потенциальная энергия тела в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где — масса тела, — ускорение свободного падения, — высота положения центра масс тела над произвольно выбранным нулевым уровнем.