Виды механических движений. Вращательное движение.

Враща́тельное движе́ние — вид механического движения. При вращательном движении материальной точки она описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной

системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым.

Вращение характеризуется углом 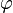, измеряющимся в градусах или радианах, угловой скоростью (измеряется в рад/с) и угловым ускорением (единица измерения — рад/с²).

При равномерном вращении (T — период вращения),

• Частота вращения (угловая частота) — число оборотов в единицу времени.

,

• Период вращения — время одного полного оборота. Период вращения 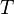и его частота связаны соотношением .

• Линейная скорость точки, находящейся на расстоянии R от оси вращения

,

• Угловая скорость вращения тела — векторная величина.

.

Динамические характеристики

Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:

.

В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы .

• Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела является Поворот — геометрическое преобразование

5) Инерциальные системы отсчета. Преобразования Галилея.

При́нцип относи́тельности — фундаментальный физический принцип, согласно которому все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.

Отсюда следует, что все законы природы одинаковы во всех инерциальных системах отсчёта.

Различают принцип относительности Эйнштейна (который приведён выше) и принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимость преобразований Галилея, оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике.

В современной литературе принцип относительности в его применении к инерциальным системам отсчета (чаще всего при отсутствии гравитации или при пренебрежении ею) обычно выступает терминологически как лоренц-ковариантность (или лоренц-инвариантность) .

Отцом принципа относительности считается Галилео Галилей, который обратил внимание на то, что находясь в замкнутой физической системе, невозможно определить, покоится эта система или равномерно движется. Во времена Галилея люди имели дело в основном с чисто механическими явлениями. В своей книге «Диалоги о двух системах мира» Галилей сформулировал принцип относительности следующим образом:

Для предметов, захваченных равномерным движением, это последнее как бы не существует и проявляет своё действие только на вещах, не принимающих в нём участия.

Идеи Галилея нашли развитие в механике Ньютона. Однако с развитием электродинамики оказалось, что законы электромагнетизма и законы механики (в частности, механическая формулировка принципа относительности) плохо согласуются друг с другом, так как уравнения механики в известном тогда виде не менялись после преобразований Галилея, а уравнения Максвелла при применении этих преобразований к ним самим или к их решениям — меняли свой вид и, главное, давали другие предсказания (например, измененную скорость света) . Эти противоречия привели к открытию преобразований Лоренца, которые делали применимым принцип относительности к электродинамике (сохраняя инвариантной скорость света) , и к постулированию их примененимости также к механике, что затем было использовано для исправления механики с их учетом, что выразилось, в частности, в созданной Эйнштейном Специальной теории относительности. После этого обобщённый принцип относительности (подразумевающий применимость и к механике, и к электродинамике, а также к возможным новым теориям, подразумевающий также преобразования Лоренца для перехода между инерциальными системами отсчета) стал называться «принципом относительности Эйнштейна» , а его механическая формулировка — «принципом относительности Галилея» .