Волновая функция, некоторые ее свойства, плотность вероятности. Уравнение Шредингера.

Волнова́я фу́нкция, или пси-функция 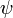— комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

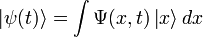
где 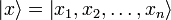— координатный базисный вектор, а 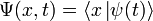— волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

Волновая функция динамических переменных и времени определяет состояние системы точностью до фазового множителя. Т. е.

т. е. , описывает одно и тоже состояние, где - фазовый множитель.

Волновая функция - комплексная, непрерывная, конечная. У нее почти всюду существует конечная производная по координате, но в некоторых точках может терпеть скачек (особые точки).

Функции - нормируемые, т.е. квадратично интегрируемы. Но для свободной материальной точки не нормируема.

- элементарный объем

- вероятность того, что динамические переменные лежат в интервале .

Это определение справедливо для квадратично интегрируемых функций.

Для не квадратично интегрируемых функций величина пропорциональна плотности вероятности

Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве (в общем случае, в конфигурационном пространстве) и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике. Установлено Эрвином Шрёдингером в 1926 году.

Уравнение Шрёдингера предназначено для частиц без спина, движущихся со скоростями много меньшими скорости света. В случае быстрых частиц и частиц со спином используются его обобщения (уравнение Клейна — Гордона, уравнение Паули, уравнение Дирака и др.)

В начале XX века учёные пришли к выводу, что между предсказаниями классической теории и экспериментальными данными об атомной структуре существует ряд расхождений. Открытие уравнения Шрёдингера последовало за революционным предположением де Бройля, что не только свету, но и вообще любым телам (в том числе и любым микрочастицам) присущи волновые свойства.

Исторически окончательной формулировке уравнения Шрёдингера предшествовал длительный период развития физики. Оно является одним из важнейших уравнений физики, объясняющих физические явления. Квантовая теория, однако, не требует полного отказа от законов Ньютона, а лишь определяет границы применимости классической физики. Следовательно, уравнение Шрёдингера должно согласовываться с законами Ньютона в предельном случае.