Квантовая теория строения атома водорода (по Бору).Объяснение спектров излучения и поглощения водорода. Квантовые числа. Принцип Паули. Правила отбора.

Исходя из этих постулатов и используя планетарную модель строения атома, Н. Бор разработал количественную теорию атома водорода. Он рассчитал радиусы стационарных орбит электрона в атоме водорода и вычислил соответствующие им значения энергии.

Расчет радиусов орбит.' Электрон движется вокруг ядра в атоме водорода по круговой орбите под действием кулоновской силы, которая сообщает ему центростремительное ускорение. По второму закону Ньютона F ⃗ =ma ⃗ .

Центростремительное ускорение a cs =υ 2 r электрону сообщает кулоновская сила притяжения со стороны ядра F=e 2 4πε 0 r 2 . Следовательно,

mυ 2 r =e 2 4πε 0 r 2 , откуда mυ 2 =e 2 4πε 0 r 2 .

Согласно III постулату Бора mυr=nh 2π , отсюда υ=nh 2πmr .

Из уравнений (20.1) и (20.2) получим mn 2 h 2 4π 2 m 2 r 2 =e 2 4πε 0 r 2 v .

Откуда r=n 2 h 2 ε 0 πme 2 —

выражение для радиусов разрешенных стационарных орбит электрона в атоме водорода. Здесь n — номер орбиты, радиус которой r, ε 0— электрическая постоянная, h — постоянная Планка, m — масса электрона, е — заряд электрона.

Мы видим, что радиусы стационарных устойчивых орбит возрастают пропорционально квадратам номеров орбит

r 1 :r 2 :r 3 ⋯=1 2 :2 2 :3 2

и т.д. Если электрон в атоме водорода находится на одной из стационарных орбит, то атом обладает определенным значением энергии, определяемой энергией электрона:

W=W k +W n =mυ 2 2 −e 2 4πε 0 r 2 v .

(Знак "-" перед потенциальной энергией означает, что за W n =0 принято то значение, которое соответствует r=∞). Подставив в эту формулу значения υ и r из формул (20.2) и (20.3), получим:

W=m 2 n 2 h 2 4π 2 m 2 r 2 −e 2 4πε 0 r 2 =n 2 h 2 π 2 m 2 e 2 8π 2 mn 4 h 4 ε 2 0 −e 2 πme 2 4πε 0 n 2 h 2 ε 0 =me 4 8πε 0 vn 2 h 2 .

Таким образом, энергия электрона, находящегося на n-й орбите,

W=−me 4 8πε 0 vn 2 h 2 . (20.4)

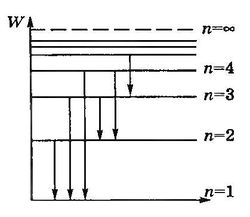
Из этой формулы видно, что значения энергии атома водорода квантованы и, чем больше n, тем больше энергия W_n. Для наглядного представления возможных энергетических состояний атомов используются энергетические диаграммы, на которых каждое стационарное состояние атома отмечается горизонтальной линией, называемой энергетическим уровнем . Ниже всех на диаграмме располагается энергетический уровень, соответствующий основному состоянию (состояния с минимальной энергией). Энергетические уровни возбужденных состояний располагаются над основным уровнем на расстояниях, пропорциональных разности энергий возбужденного и основного состояний. Переходы атома из одного состояния в другое изображаются вертикальными линиями между соответствующими уровнями на диаграмме. Направление перехода обозначается стрелкой. При переходе электрона с k-й на n-ю орбиту излучается фотон с частотой

ν kn =W k −W n h =me 4 8ε 2 0 h 3 (1 n 2 −1 k 2 ).

Сравнивая это выражение с эмпирической формулой

ν kn =R(1 n 2 −1 k 2 ),

видим, что постоянная Ридберга R=me 4 8ε 2 0 h 3 ; следовательно, в формуле k — номер орбиты, с которой происходит переход электрона в атоме, n — номер орбиты, на которую переходит электрон.

Исследования спектров излучения разреженных газов (т. е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома - атома водорода.

Швейцарский ученый И. Бальмер (1825-1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:

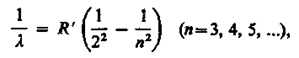(209.1)

где R' = 1,10×10⁷ м^-1-постоянная Ридберга^*. Так как v=c/A, то формула (209.1) может быть переписана для частот:

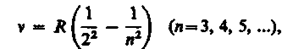(209.2)

где R = R'с = 3,29×10¹⁵ с^-1 - также постоянная Ридбeрга.

Из выражений (209.1) и (209.2) вытекает, что спектральные линии, отличающиеся различными значениями л, образуют группу или серию линий, называемую серией Бальмера.С увеличением л линии серии сближаются; значение n = ¥ определяет границу серии, ккоторой со стороны больших частот примыкает сплошной спектр.

В дальнейшем (в начале XX в.) в спектре атома водорода было обнаружено еще несколько серий. В ультрафиолетовой области спектра находится серия Лаймана:

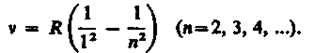
В инфракрасной области спектра были также обнаружены:

42.

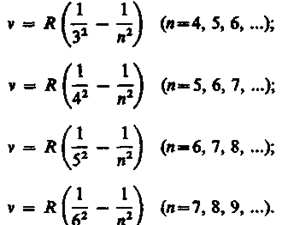
Серия Пашена

44.

45.

Серия Брэкета

47.

48.

Серия Пфунда

50.

51.

Серия Хэмфри

53.

Все приведенные выше серив в спектре атома водорода могут быть описаны одной формулой, называемой обобщенной формулой Бальмера:

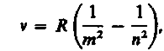(209.3)

где т имеет в каждой данной серии постоянное значение, т= 1, 2, 3, 4, 5, 6 (определяет серию), п принимает целочисленные значения начиная с т+1 (определяет отдельные линии этой серии).

Исследование более сложных спектров - спектров паров щелочных металлов (на пример, Li, Na, К) - показало, что они представляются набором незакономерно расположенных линий. Ридбергу удалось разделить их на три серии, каждая из которых располагается подобно линиям бальмеровской серии.

Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью. Приведенный выше вид сериальных формул, удивительная повторяемость в них целых чисел, универсальность постоянной Ридберга свидетельствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физики оказалось невозможным.

Ква́нтовое число́ в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы.

Некоторые квантовые числа связаны с движением в пространстве и характеризуют вид волновой функции частицы. Это, например, радиальное (главное) ( 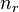), орбитальное ( 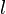) и магнитное ( 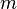) квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента и его проекция на заданную ось, соответственно.

Некоторые другие квантовые числа никак не связаны с перемещением в обычном пространстве, а отражают «внутреннее» состояние частицы. К таким квантовым числам относится спин и его проекция. В ядерной физике вводится также изоспин, а в физике элементарных частиц появляется цвет, очарование, прелесть (или красота^[1]) и истинность.

Принцип Паули является следствием свойства симметрии волновой функции тождественных фермионов. Частицы с полуцелым спином − фермионы (электроны, кварки, протоны, нейтроны, ядра с нечетным числом нуклонов) - подчиняются статистике Ферми-Дирака. Поэтому для тождественных фермионов волновая функция должна быть антисимметрична относительно их перестановки

ψ(2,1,..., A) = -ψ(1,2,..., A).

(1)

Если частицы 1 и 2 находятся в одинаковом состоянии, то ψ(2,1,..., A) = ψ(1,2,..., A), что противоречит (1) и возможно только в случае, если ψ(2,1,..., A) = ψ(1,2,..., A) ≡ 0. То есть в системах, подчиняющихся статистике Ферми-Дирака и описываемых антисимметричными волновыми функциями, не должно существовать двух тождественных частиц с полностью совпадающими квантовыми характеристиками. Это утверждение впервые было сформулировано В. Паули и называется принципом Паули.

42.Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских характеристических спектров. Закон Мозли.

Точно так же, как и в атоме водорода, в более сложных атомах электроны могут двигаться вокруг ядра только по определенным избранным орбитам. Различные экспериментальные данные указывают, что возможные орбиты электронов в атоме группируются в систему оболочек. Грубо схематически можно представить себе эти оболочки в виде концентрических сфер, окружающих ядро. Каждая из оболочек содержит определенное число орбит, на каждой из которых может находиться только один электрон. Оболочка наименьшего радиуса, называемая 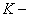оболочкой, содержит две орбиты. На второй оболочке — 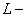оболочке — имеется восемь орбит. Столько же орбит на следующей оболочке — третьей. Далее идет четвертая оболочка с 18 орбитами и т. д.

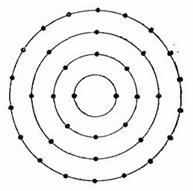
. Условная схема электронных оболочек атома: число черных точек равно наибольшему возможному числу электронов на оболочке

Как указало в предыдущем параграфе, при переходе электрона с орбиты большего радиуса на орбиту меньшего радиуса выделяется энергия. Электрон, находящийся на внешней оболочке, обязательно «перескочит» на внутреннюю, если только на ней имеется свободная орбита. Поэтому в невозбужденном многоэлектронном атоме все электроны сосредоточены на внутренних орбитах.

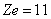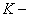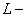Рассмотрим, например, элемент с порядковым номером 11 — натрий. Заряд атомного ядра натрия равен - натрий. Атом натрия содержит 11 электронов: 10 из этих электронов заполняют все наличные орбиты на и оболочках, а последний 11 - й электрон находится на третьей оболочке (рис. 369).

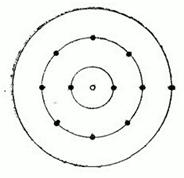
Схема атома натрия: светлый кружок — ядро атома, черные точки — электроны. Заполнены все места на 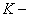и 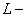оболочках и одни электрон находится на третьей оболочке

Внешние электроны атома связаны с ядром значительно слабее внутренних. Во-первых, они находятся на гораздо большем расстоянии от ядра. Во-вторых, сила притяжения внешних электронов положительным ядром в большой степени компенсируется отталкиванием со стороны отрицательных электронов, расположенных на внутренних оболочках. Как показывают измерения, чтобы оторвать от атома один из внешних электронов, нужна энергия 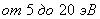в зависимости от рода атома. Для того чтобы перевести какой-либо внешний электрон на одну из более далеких оболочек, не отрывая его от атома (т. е. для возбуждения атома), достаточна еще меньшая энергия. При возвращении такого электрона на более близкую к ядру оболочку будет испущен световой квант с энергией, не превышающей 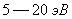, т. е. с длиной волны, лежащей в области видимого или ультрафиолетового света. Испускание света в оптических областях спектра связано, таким образом, с поведением внешних электронов атома.

Для отделения от атома внутренних электронов нужна гораздо большая энергия, быстро растущая с увеличением заряда атомного ядра. Так, чтобы вырвать электрон из 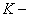оболочки, нужна энергия около 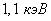для натрия 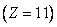, свыше 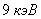для меди 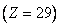, около 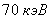для вольфрама 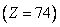. Переход электронов с 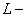оболочки и следующих за ней оболочек на свободное место в 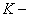оболочке приводит поэтому к испусканию квантов большой энергии (с малой длиной волны), соответствующей рентгеновскому излучению.

Ранее уже указывалось, что рентгеновское излучение представляет собой электромагнитное излучение, возникающее при резком торможении электронов в веществе (тормозное излучение). Теперь мы видим, что существует второй механизм испускания рентгеновского излучения, состоящий в следующем. Электронная бомбардировка анода в рентгеновской трубке приводит к вырыванию электронов из внутренних оболочек атомов, составляющих анод. На освободившиеся места переходят электроны из внешних оболочек тех же атомов; при таких переходах испускается рентгеновское излучение, получившее название характеристического рентгеновского излучения данного атома.

Закон Мозли — закон, связывающий частоту спектральных линий характеристического рентгеновского излучения атома химического элемента с его порядковым номером. Экспериментально установлен английским физиком Генри Мозли в 1913 году.

Формулировка закона Мозли

Согласно Закону Мозли, корень квадратный из частоты 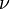спектральной линии характеристического излучения элемента есть линейная функция его порядкового номера :

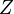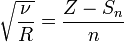
где 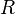— постоянная Ридберга, 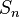— постоянная экранирования, 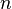— главное квантовое число. На диаграмме Мозли зависимость от 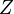представляет собой ряд прямых (К-, L-, М- и т. д. серии, соответствующие значениям n = 1, 2, 3,...).

Закон Мозли явился неопровержимым доказательством правильности размещения элементов в периодической системе элементов Д. И. Менделеева и содействовал выяснению физического смысла .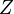

В соответствии с Законом Мозли, рентгеновские характеристические спектры не обнаруживают периодических закономерностей, присущих оптическим спектрам. Это указывает на то, что проявляющиеся в характеристических рентгеновских спектрах внутренние электронные оболочки атомов всех элементов имеют аналогичное строение.

Более поздние эксперименты выявили некоторые отклонения от линейной зависимости для переходных групп элементов, связанные с изменением порядка заполнения внешних электронных оболочек, а также для тяжёлых атомов, появляющиеся в результате релятивистских эффектов (условно объясняемых тем, что скорости внутренних электронов сравнимы со скоростью света).

В зависимости от ряда факторов — от числа нуклонов в ядре атома (изотопический сдвиг), состояния внешних электронных оболочек (химический сдвиг) и пр. — положение спектральных линий на диаграмме Мозли может несколько изменяться. Изучение этих сдвигов позволяет получать детальные сведения об атоме.