Силы, действующие в жидкости. Давление

Жидкость в гидравлике рассматривают как сплошную среду без пустот и промежутков. Кроме того, не учитывают влияние отдель­ных молекул, т. е. даже бесконечно малые частицы жидкости счи­тают состоящими из весьма большого количества молекул.

Из курса физики известно, что вследствие текучести жидко­сти, т. е. подвижности ее частиц, она не воспринимает сосредото­ченные силы. Поэтому в жидкости действуют только распределен­ные силы, причем эти силы могут распределяться по объему жид­кости или по поверхности. Первые называются массовыми, или объемными, а вторые — поверхностными.

К объемным (массовым) силам относятся силы тяжести и силы инерции. Они пропорциональны массе и подчиняются второму закону Ньютона.

К поверхностным силам следует отнести силы, с которыми воздействуют на жидкость соседние объемы жидкости или тела, так как это воздействие осуществляется через поверхности. Учи­тывая важность поверхностных сил в гидравлике, рассмотрим их подробнее.

Пусть на плоскую поверхность площадью A под произвольным углом действует сила F (рис. 1). Силу R можно разложить на тан­генциальную Т и нормальную R составляющие.

Тангенциальная составляющая называется силой трения Т и вызывает в жидкости касательные напряжения (или напряжения трения):

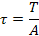
Нормальная сила F называется силой давления и вызывает в жидкости нормальные напряжения сжатия, которые определяют­ся отношением

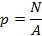
Единицей измерения касательных напряжений в системе СИ является паскаль (Па) — ньютон, отнесенный к квадратному мет­ру (1 Па = 1 Н/м²).

Эти нормальные напряжения сжатия называются гидромехани­ческим давлением или просто давлением. Рассмотрим системы от­счета давления и единицы его измерения.

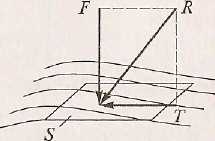
Рисунок 1.

Важным при решении практических задач является выбор сис­темы отсчета давления (шкалы давления). За начало шкалы может быть принят аб­солютный нуль давления (аналог абсолют­ного нуля температуры) — 0_абс. При отсче­те давлений от этого нуля их называют аб­солютными р_а5с (рис. 2, а).

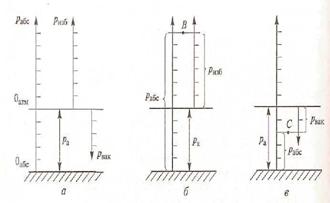
Рисунок 2 - Системы отсчета давления:

шкалы давления; 6 — взаимосвязь абсолютного и избыточного давлений; в взаимосвязь абсолютного давления и давления вакуума

Однако, как показывает практика, технические задачи удобнее решать, ис­пользуя избыточные давления р_изб, т.е. когда за начало шкалы принимается атмосферное давление — 0_ата (см. рис.2, а).

Давление, которое отсчитывается «вниз» от атмосферного нуля, называется давлением вакуума p_вaк, или вакуумом (см. рис.2, а).

Таким образом, существуют три шкалы для отсчета давления, т.е. давление может быть абсолютным, избыточным или вакуум­ным. Получим формулы для пересчета одного давления в другое.

Для получения формулы пересчета избыточного давления в аб­солютное р_а6с воспользуемся рис. 2, б. Пусть значение искомого давления определяется положением точки В. Тогда очевидно, что

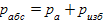
где р_а — атмосферное давление, измеренное барометром.

Связь между абсолютным давлением р_абс и давлением вакуума р_вак можно установить аналогичным путем, но уже исходя из поло­жения точки С (рис. 2, в):

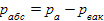
И избыточное давление, и вакуум отсчитываются от одного нуля (0_атм), но в разные стороны. Следовательно,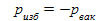

Таким образом, формулы приведенные выше связывают абсолютное, избыточное и вакуумное давления и позволяют пересчитать одно в другое. Практика показала, что для решения технических (при­кладных) задач наиболее удобно использовать избыточные давле­ния.

Основной единицей измерения давления в системе СИ является паскаль (Па), который равен давлению, возникающему при дей­ствии силы в 1 Н на площадь размером 1 м² (1 Па = 1 Н/м²). Однако чаще используются более крупные единицы: килопаскаль (1 кПа = - 10³ Па) и мегапаскаль (1 МПа = 10⁶ Па).

В технике широкое распространение получила внесистемная единица — техническая атмосфера (ат), которая равна давлению, возникающему при действии силы в 1 кгс на площадь размером 1 см² (1 ат = 1 кгс/см²). Соотношения между наиболее использу­емыми единицами следующие:

10 ат = 0,981 МПа » 1 МПа или 1 ат - 98,1 кПа » 100 кПа.

В зарубежной литературе используется также единица измере­ния давления бар ( бар = 10⁵ Па).

2.2. Основное уравнение гидростатики

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила - сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

Пусть жидкость содержится в сосуде (рис.3) и на ее свободную поверхность действует давление P₀ . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

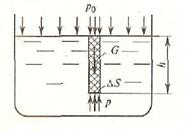Рис. 3. Схема для вывода основного уравнения гидростатики

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

PdS - P₀ dS - ρghdS = 0

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем

P = P₀ + ρgh = P₀ + hγ

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P₀. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.

Давление жидкости на стенки

При расчетах на прочность различных гидромеханических соору­жений возникает необходимость определения давления жидкости на стенку и дно этих сооружений.

Избыточное давление жидкости на единицу площади плоской стенки равно

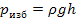
Полная сила, действующая на плоскую стенку, равна произве­дению величины смоченной площади стенки A_см на гидростатическое давление в ее центре тяжести:

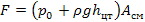
В открытом сосуде при р_о = 0 полная сила давления

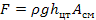
где 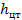— глубина погружения центра тяжести площади, м;

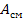— смоченная площадь стенки, м².

Точка приложения силы Р называется центром давления. Центр давления обычно лежит ниже центра тяжести стенки. Для прямо­угольной стенки, например, центр тяжести находится на расстоянии половины высоты от основания, а центр давления — на расстояния одной трети высоты.

Частным случаем криволинейной стенки являются стенки цилин­дрических резервуаров, котлов, труб и др.

Полная сила давления, действующая на цилиндрическую поверх­ность,

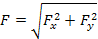
где Р_х — горизонтальная составляющая, равная силе давлений жидкости на вертикальную проекцию цилиндрической поверхно­сти, Н:

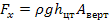
Р_у — вертикальная составляющая силы давления Н, равная силе тяжести действующей в объеме тела давления V:

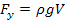
Объемом тела давления V 'называется объем жидкости, ограни­ченный сверху свободной поверхностью жидкости, снизу — рассма­триваемой криволинейной поверхностью, а с боков — вертикальной поверхностью, проведенной через периметр, ограничивающий стенку.

Направление полной силы давления F определяется углом, обра­зуемым вектором F с горизонтальной плоскостью

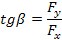
Для цилиндрического резервуара с вертикальной осью верти­кальная составляющая F_у равна нулю, поэтому полная сила давле­ния на боковую поверхность равна F_х

Закон Архимеда

На любое тело, погруженное в жидкость, действует выталкиваю­щая сила, равная силе тяжести жидкости, вытесненной этим телом

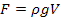
где F — выталкивающая (архимедова) сила, Н;

r — плотность жидкости, кг/м³;

g — ускорение свободного падения, м/с²;

V — объем погруженной части тела, м³.

Произведение rV называют водоизмещением.

В зависимости от соотношения между силой тяжести тела и силой тяжести вытесненной им жидкости возможны три состоя­ния тела:

1. Сила тяжести тела больше силы тяжести вытесненной жид­кости

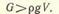
Такое тело будет тонуть.

2. Сила тяжести тела равна силе тяжести вытесненной жидкости

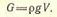
В этом случае тело будет плавать.

3. Сила тяжести тела меньше силы тяжести вытесненной жидкости

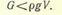
При таком соотношении тело будет всплывать.

Задача №3 К резервуару, заполненному минеральным маслом, присоеди­нен пьезометр. Абсолютное давление на поверхности жидкости в резервуаре р₀ = 1,18 кг/см². Определить плотность минерального масла, если высота его подъема в трубке пьезометра h = 2,0 м.

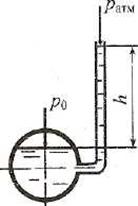
Составим уравнение

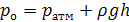
Путем преобразования получаем

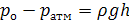
Выразим плотность минерального масла ( при подстановке значений важно помнить, что значение давления необходимо перевести из кг/см² в паскали: 1 кг/см² = 10⁵ Па)

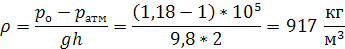
Задача №4 Определить горизонтальную силу, действующую на плотину длиной L=1000 м при высоте воды перед плотиной Н=100 м

Решение

Сила действующая на плотину определяется по формуле

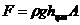
где r - плотность воды, r=1000 кг/м³;

g – ускорение свободного падения , g = 9,8 м/с²

h_цт – положение центра тяжести смоченной поверхности, ;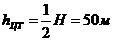

А – площадь смоченной поверхности, А=L*H=1000*100=100000 м²

тогда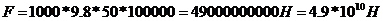

Задача №5 Определить силу, действующую на деревянный брусок длиной L=50 см и поперечным сечением 30 на 5 см, полностью погруженный в воду. Плотность древесины принять равной r_д=600 кг/м³.

Решение Сила, действующая на брусок, полностью погруженный в воду, равна разности между выталкивающей силой F_в и весом бруска G

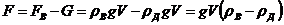
где V – объем деревянного бруска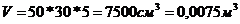

Тогда сила действующая на брусок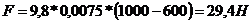

Раздел 3. Основные понятия и определения гидродинамики

Уравнения кинематики и динамики жидкости весьма значи­тельно отличаются от аналогичных уравнений для твердого тела. Это вызвано прежде всего особенностями исследуемого объекта, т. е. жидкости, частицы которой не имеют жесткой связи между со­бой. Отсутствие жесткой связи существенно усложняет рассмотре­ние процессов, происходящих в жидкости. Для упрощения изуче­ния течений в гидромеханике широко используется так называемая идеальная жидкость. Под этим термином понимают не существу­ющую в природе абсолютно невязкую жидкость. Тогда происходя­щие явления сначала исследуются применительно к идеальной жид­кости, а затем полученные закономерности переносятся с введени­ем корректирующих поправок на потоки реальных жидкостей.

Течение жидкости, как и любое другое движение, может быть установившимся и неустановившимся. При установившемся тече­нии все физические параметры в данной точке потока (скорость, давление и др.) остаются неизменными во времени. Примером ус­тановившегося течения может служить истечение через отверстие в дне сосуда, в котором поддерживается постоянный уровень жид­кости. При неустановившемся течении физические параметры в данной точке потока (или некоторые из них) меняются во време­ни. Для примера можно привести рассматриваемое выше истече­ние, но без поддержания постоянного уровня жидкости в сосуде, т. е. истечение до полного опорожнения. В дальнейшем будут рас­сматриваться в основном устано­вившиеся течения жидкости.

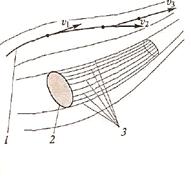
Большое значение в механике жидкости имеет термин «линия тока». Под этим понимают услов­ную линию в потоке жидкости, проведенную так, что вектор ско­рости в любой ее точке направлен по касательной (линия 1 на рис. 3.1). При установившемся течении ли­ния тока совпадает с траекторией движения частицы жидкости. Не­обходимо также отметить, что при установившемся точении в любой

точке потока существует только одна (неизменная во времени) скорость. Поэтому через данную точку может проходить только одна линия тока. Следовательно, линии тока при установившемся тече­нии не могут пересекаться.

Если в потоке жидкости взять замкнутую линию 2 (см. рис. 3.1), состоящую из бесконечного множества точек, и через каждую из этих точек провести линию тока 3, то множество этих линий обра­зуют трубчатую поверхность. Такую поверхность принято называть трубкой тока, а часть потока внутри этой поверхности — струйкой. Струйку жидкости бесконечно малой толщины принято называть элементарной струйкой.

Как было отмечено ранее, при установившемся течении линии тока не пересекаются и, следовательно, ни одна линия тока не может пронизывать трубку тока (иначе она пересечет одну из ли­ний, образующих эту трубку). Следовательно, ни одна частица жид­кости не может проникнуть внутрь трубки, тока или выйти из нее. Таким образом, выделенная трубка тока при установившемся те­чении является непроницаемой стенкой для жидкости.

Сечениями потока (или струйки) жидкости принято называть поверхности, нормальные к линиям тока. Например, поверхность, ограниченная замкнутым контуром 2 (затемнена на рис 3.1), являетсясечением для струйки в пределах трубки тока линий 3. При параллельно струйном течении сечения представляют собой плос­кости, перпендикулярные направлению движения жидкости. Сеченияпотоков или струй жидкости иногда также называют живы­ми сечениями

Различают напорные и безнапорные течения жидкости. Напор­ными называют течения в закрытых руслах без свободной поверх­ности, а безнапорными — течения со свободной поверхностью.