Циклы поршневых двигателей внутреннего
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Смоленская государственная сельскохозяйственная академия»
А.Г. Никифоров, Д.Ю. Попова
ЦИКЛЫ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ
ВНУТРЕННЕГО СГОРАНИЯ
Учебно-методическое пособие по теплотехнике
Смоленск 2017
УДК 621.432
ББК 22.317
Н62
Рецензент: кандидат технических наук, доцент, заведующий кафедрой Промышленной теплоэнергетики ФГБОУ ВО НИУ МЭИ, филиал в г.Смоленске, Михайлов В.А.
Никифоров А.Г., Попова Д.Ю.
Н62 Циклы поршневых двигателей внутреннего сгорания. Учебно-методическое пособие по теплотехнике / А.Г. Никифоров, Д.Ю. Попова. – Смоленск: Изд-во ФГБОУ ВО Смоленской ГСХА 2017. – 73 с.
Рассмотрены основные теоретические положения, определяющие работу двигателей внутреннего сгорания, изложены требования по выполнению и защите расчетной работы. Рекомендована последовательность выполнения расчета. Приведен алгоритм решения индивидуальных заданий, справочные материалы и тестовые вопросы для самоподготовки.
Учебно-методическое пособие предназначено для самостоятельной работы студентов очной и заочной формы обучения, обучающихся по направлению подготовки 35.03.06 Агроинженерия.
Печатается по решению методического совета ФГБОУ ВО Смоленская ГСХА (протокол №___ от _______2016).
УДК 621.432
ББК 22.317
© Никифоров А.Г., Попова Д.Ю.
© Федеральное государственное бюджетное образовательное учреждение высшего образования «Смоленская государственная сельскохозяйственная академия», 2017
ПРЕДИСЛОВИЕ
Основной задачей дисциплины Теплотехника для студентов направления подготовки 35.03.06 Агроинженерия является комплекс знаний об основных законах термодинамики и применения этих знаний для расчета циклов двигателей внутреннего сгорания (ДВС).
Студент должен уметь решать типовые задачи, выполнять основные расчеты и анализировать работу тепловых машин при работе по разным термодинамическим циклам, самостоятельно выбирать оптимальные режимы работы для двигателей внутреннего сгорания.
Учебное пособие состоит из трех основных разделов: теоретического «Циклы поршневых двигателей внутреннего сгорания», практического «Пример задания для расчета» и раздела для самостоятельного контроля усвоенного материала «Вопросы и задания для проверки знаний».
Выполнение индивидуального задания позволит студенту получить практические навыки расчёта теоретического цикла ДВС. Тестовые вопросы помогут студенту провести проверку собственных теоретических знаний. Подготовка к тестированию выполняется студентом самостоятельно. Вопросы, предлагаемые в тестах, освещены в литературе, список которой приведен в данном пособии. В пособии приведены алгоритмы и необходимые справочные данные для выполнения индивидуальной расчетной работы.
ЦИКЛЫ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО
СГОРАНИЯ
Двигатели внутреннего сгорания являются основным мобильным энергетическим средством большинства сельскохозяйственных машин.
В двигателе внутреннего сгорания (ДВС) топливо сгорает непосредственно в рабочей камере (внутри цилиндра) двигателя, в результате химическая энергия топлива преобразуется в тепловую энергию и затем в механическую работу рабочего органа двигателя (поршень).
По сравнению с двигателями внешнего сгорания (паровыми машинами) ДВС:
• не имеет дополнительных элементов теплопередачи — топливо, сгорая, само образует рабочее тело;
• компактнее, так как не имеет целого ряда дополнительных агрегатов;
• легче;
• экономичнее;
• потребляет газообразное или жидкое топливо, обладающее определенными заданными параметрами (испаряемостью, температурой вспышки паров, плотностью, теплотой сгорания, октановым или цетановым числом), так как от этих свойств зависит сама работоспособность ДВС.
Наибольшее распространение получили поршневые двигатели внутреннего сгорания. В поршневых двигателях камера сгорания находится в цилиндре, а тепловая энергия превращается в механическую с помощью кривошипно-шатунного механизма.
Все современные поршневые двигатели внутреннего сгорания разделяются по организации процесса сгорания топлива на три основные группы:
1) со сгоранием топлива при постоянном объеме ν=const (цикл Отто);
2) со сгоранием топлива при постоянном давлении p=const (цикл Дизеля);
3) со смешанным сгоранием топлива: частично при постоянном объеме и частично при постоянном давлении (цикл Сабатэ-Тринклера).
Для проведения термодинамического анализа эффективности работы циклов можно считать, что в этих процессах к рабочему телу подводится теплота q1, поэтому зачастую эти термодинамические циклы называют соответственно: с изохорным подводом теплоты, с изобарным подводом теплоты, со смешанным подводом теплоты. Во всех указанных циклах отвод теплоты q2 осуществляется по изохоре ba, рисунок 1.
а) 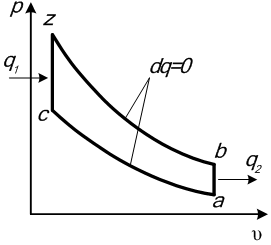 б)
б) 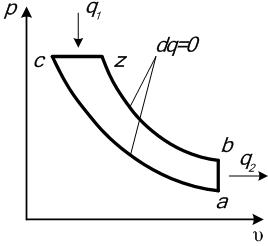
в) 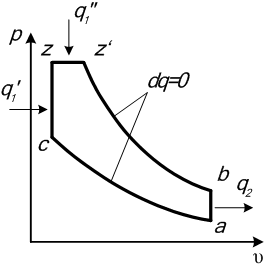
Рисунок 1 – Циклы поршневых ДВС в p,υ-диаграмме:
а) с подводом теплоты при постоянном объеме,
б) с подводом теплоты при постоянном давлении, в) со смешанным подводом теплоты
Идеальные циклы применяют для исследования действительных циклов, происходящих в реальных двигателях, и сравнения по степени использования тепла различных типов двигателей, независимо от их конструктивных особенностей. Рассмотрим подробнее.
Идеальным термодинамическим циклом двигателя называется круговой замкнутый обратимый цикл, представляющий собой совокупность последовательных процессов, совершаемых идеальным газом в цилиндре идеальной машины.
Обратимый цикл – последовательность процессов перехода термодинамической системы из одного состояния в другое, допускающий возможность возвращения системы в первоначальное состояние через ту же последовательность промежуточных состояний, что и в прямом цикле, но проходимых в обратном порядке.
Очевидно, что идеальные циклы ДВС лишь приближенно отражают известные из опыта особенности реальных процессов, происходящих в работающем двигателе.
Но для упрощения расчетов принимаются следующие допущения:
1) с идеальным газом, находящимся в цилиндре, совершаются только физические, по не химические изменения, т. е. состав и масса газа остаются постоянными;
2) теплоемкость газа не изменяется в термодинамических процессах цикла;
3) тепло подводится к газу извне, а не в процессе сгорания топлива в цилиндре;
4) процессы сжатия и расширения совершаются по адиабатам, т. е. без теплообмена с внешней средой (стенки цилиндра теплонепроницаемые и трение между поршнем и стенками цилиндра отсутствует);
5) выпуск отработавших газов заменяется передачей некоторого количества тепла холодному источнику при постоянном объеме.
Термодинамическое исследование идеальных циклов поршневых ДВС состоит в получении аналитических выражений термического коэффициента полезного действия (КПД) и среднего теоретического давления цикла, а также выявлении характера зависимости этих показателей от параметров цикла.
Основными характеристиками или параметрами любого цикла ДВС являются следующие безразмерные величины:
степень сжатия:
ε = υa/υc, (1)
представляющая собой отношение удельного объема рабочего тела в точке а (это положение поршня в цилиндре принято называть нижней мёртвой точкой - НМТ) к его удельному объему в конце процесса сжатия (точка с – верхняя мёртвая точка – ВМТ, объем камеры сгорания);
степень повышения давления:
λ = pz/pc , (2)
представляющая отношение давлений в конце и в начале изохорного процесса подвода теплоты;
степень предварительного расширения, или степень изобарного расширения:
ρ = υz’/υc , (3)
представляющая собой отношение объемов в конце и в начале изобарного процесса подвода теплоты (рисунок 1). [4]
Степень совершенства преобразования тепловой энергии в механическую работу в термодинамическом цикле двигателя оценивается безразмерной величиной – термическим коэффициентом полезного действия ηt(его также называют тепловым или термодинамическим). В общем случае, термический КПД – это отношение работы, совершенной в прямом обратимом термодинамическом цикле, к теплоте, сообщенной рабочему телу от внешних источников.
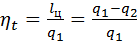 , (4)
, (4)
гдеlЦ – это тепло, преобразованное в цикле в работу, lЦ = 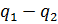 .
.
Термический КПД термодинамического цикла показывает, какое количество получаемой теплоты машина превращает в работу в конкретных условиях протекания идеального цикла. Чем больше величина ηt, тем совершеннее цикл и тепловая машина.
В инженерных расчётах для вычисления мощности ДВС часто используется понятие среднего теоретического давления цикла рt, это условное постоянное давление, под действием которого поршень в течение одного хода совершает работу, равную работе всего теоретического цикла. [3] Среднее теоретическое давление цикла является отношением работы цикла lЦ к рабочему объёму двигателя υh= υНМТ – υВМТ = υa–υc:
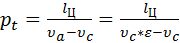 , (5)
, (5)
Таким образом, среднее давление цикла pt, представляет собой работу, полученную с единицы объема, т.е. является удельной работой. В теории тепловых двигателей υc= υВМТ= υmin называют объемом камеры сгорания. Отношение q1/υc, имеющее размерность Дж/м3, характеризует тепловую нагрузку единицы объема камеры сгорания.
Учитывая, что υc=υвмт=υmin, преобразуем выражение (5) к виду:
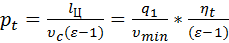 , (6)
, (6)
При исследовании идеальных термодинамических циклов поршневых ДВС обычно определяют количество подведенной и отведенной теплоты, работу расширения и работу сжатия, основные параметры состояния рабочего тела в характерных точках цикла, изменение внутренней энергии и энтропии рабочего тела, вычисляют и производят анализ термического КПД цикла.
Цикл Отто
В двигателях легкого топлива с искровым зажиганием время сгорания очень мало, поэтому в термодинамической постановке подвод теплоты принято считать происходящим при постоянном объеме. Идеальный термодинамический цикл с подводом теплоты при υ=const (цикл Отто) который часто называют циклом бензинового двигателя, показан на рисунке 2. [4]
а)  б)
б) 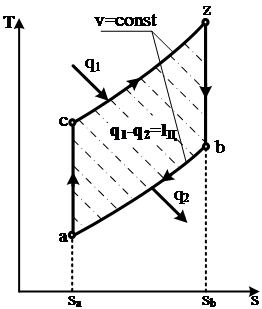
Рисунок 2 – Цикл Отто на pυ (а) и Ts-диаграммах (б)
Идеальный газ с параметрами pa,υa,Ta сжимается по изоэнтропе (адиабате) ас, в результате чего давление и температура растут. В т. с происходит зажигание смеси от электрической искры. Между точками с и zк рабочему телу подводится теплота в количестве q1. Так как сгорание происходит практически мгновенно, процесс cz можно считать изохорным. В результате давление и температура рабочего тела повышаются при постоянном объеме и в точке z достигают наибольших значений. Затем под действием продуктов сгорания с высоким давлением поршень смещается в сторону нижней мертвой точки (НМТ) при этом совершая работу расширения. Процесс zb – это адиабатное (изоэнтропное) расширение продуктов сгорания до объема НМТ (υb = υa= υНМТ). Рабочее тело в процессе zb совершает положительную работу lzb ,часть которой в дальнейшем (при повторении цикла) затрачивается на осуществление процесса ас.
В точке b открывается выпускной клапан и давление в цилиндре снижается до первоначального давления pa. В изохорном процессе ba рабочее тело при постоянном объеме возвращается в исходное состояние с отводом от него теплоты в количестве q2. Площадь под кривой zb – пропорциональна количеству работы, совершенной рабочим телом при расширении. Площадь под кривой ac пропорциональна работе, затраченной на сжатие рабочего тела. Полезная работа цикла пропорциональна площади, ограниченной на диаграмме aczb.
Ts-диаграмма используется для наглядного анализа количества подведенного q1 ( площадь saaczbsb) и отведённого q2 ( площадь saabsb) тепла и полезно использованного количества теплоты в цикле lЦ = q1 - q2 (площадь aczb).
Параметрами рассматриваемого термодинамического цикла являются:
степень сжатия:
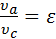 , (7)
, (7)
и степень повышения давления при изохорном подводе теплоты:
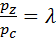 , (8)
, (8)
Количество подведенной теплоты q1 в изохорном процессе сz и ее можно определить следующим образом:
q1=сυ(Тz— Тс) , (9)
Это количество теплоты в Тs-диаграмме соответствует площади под кривой процесса cz.
Так же можно рассчитать отведенную теплоту в изохорном процессе (пропорциональна площади под кривой процесса ba):
q2=сυ(Тb—Тa) , (10)
Термический КПД цикла ηt равен отношению работы lЦ, совершаемой за цикл рабочим телом к теплоте q1, полученной при этом рабочим телом. Работа равняется разности количества подведенного и отведенного тепла к рабочему телу (lЦ = q1 – q2).
Тогда термический КПД цикла Отто с учетом выражений (9) и (10) можно представить в следующем виде:
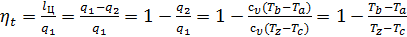 , (11)
, (11)
Выразим объем, давление и температуру в характерных точках цикла (точки c, z и b) через характеристики цикла и его начальные параметрыТа, υa, pa.
Точка с.
Удельный объём в точке сможно определить, используя определение степени сжатия:
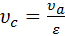 , (12)
, (12)
Процесс ac – адиабатный, тогда для него, используя уравнение адиабатного процесса,можно записать соотношение между параметрами:
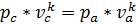
отсюда определяем давление в точке с:
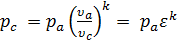 , (13)
, (13)
Аналогично, из уравнения адиабатного процесса ac:
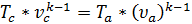
выразим температуру в точке с:
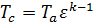 , (14)
, (14)
Точка z.
Процесс cz – изохорный.
υz 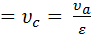 , (15)
, (15)
Из уравнения изохорного процесса, используя понятие степени повышения давления
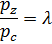
получим выражение для вычисления давления газа в точке z:
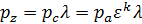 . (16)
. (16)
Для изохорного процесса отношение температур равно отношению давлений:
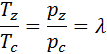
тогда выражение для температуры в точке z,с учётом выражения (14), будет иметь вид:
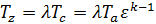 , (17)
, (17)
Точка b.
Процесс ba – изохорный, значит
υb = υa, (18)
Зная, что процесс zb – адиабатный, можно записать
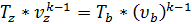
преобразуем его с учетом выражений (18) и (15) ,
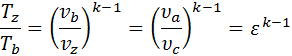
Отсюда выразим Tb , используя (17) находим температуру в точке b:
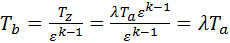 , (19)
, (19)
Так как процесс ba – изохорный, то отношение давлений равно отношению температур, т.е.:
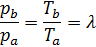
Тогда давление в точке b равняется:
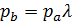 , (20)
, (20)
Таблица 1 – Расчет параметров рабочего тела в характерных точках цикла Отто
| Параметры | Характерные точки цикла | |||
| a | c | z | b | |
| v | va | 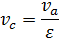 | 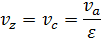 | 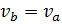 |
| p | pa | 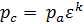 | 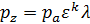 | 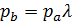 |
| T | Ta | 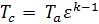 | 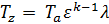 | 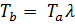 |
Подставляя выражения температур в характерных точках термодинамического цикла Отто (14), (17), (19) в выражение термического КПД цикла ηt (11) получим
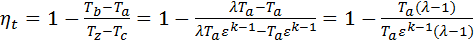 , , 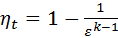 . . | (21) |
Таким образом, термический КПД цикла с подводом теплоты при постоянном объеме зависит только от степени сжатия и природы рабочего тела (k). Из уравнения (21) видно, что для рассматриваемого цикла, термический КПД тем больше, чем больше степень сжатия и показатель адиабаты. Однако если при малых степенях сжатия повышение ε вызывает существенное увеличение термического КПД, то при высоких значениях ε возрастание ηtделается все менее и менее значительным при увеличении степени сжатия, рисунок 3. С уменьшением показателя адиабаты термический КПД при той же степени сжатия уменьшается. [4]
В реальном двигателе искрового зажигания выбор степени сжатия в основном определяется практическими возможностями организации процесса сгорания без произвольной детонации (самовоспламенения смеси). В зависимости от видов топлива в таких двигателях обычно используют ε ≈ (6,5-11),pс = (0,8 - 2 МПа) (см. приложение 1). В связи с чем этот тип двигателей имеет относительно низкие КПД. Так как в уравнении (21) отсутствует параметр λ (степень повышения давления), то термический КПД цикла Отто не зависит от количества подведенной теплоты.
Работу цикла можно определить из формулы (4) подставляя значения подведённого тепла q1 (9) и выражение КПД цикла Отто (21):
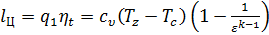 = = = = 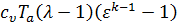 . . | (22) |
Среднее теоретическое давление цикла (5), учитывая выведенные выше зависимости (22), (7), можно определить по выражению :
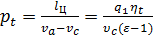 , , |
Выражая температуры Tc и Tz через Ta получим
q1= 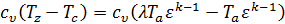 = сυТa = сυТa 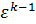 (λ – 1). (λ – 1). |
Тогда среднее теоретическое давление цикла:
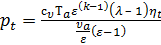 . . | (23) |
Используя уравнение Майера для идеального газа
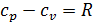 , , |
и выражение для показателя адиабаты k
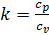 , , |
выразим удельную теплоемкость при постоянном объеме 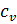 :
:
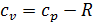 , , 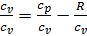 , , 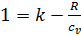 , сυ = , сυ = 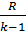 . . | (24) |
Подставляя выражение (24) в (23) среднее теоретическое давление в термодинамическом цикле Отто приводится к виду:
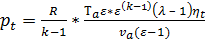 , , 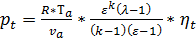 , , 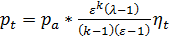 . . | (25) |
Отсюда видно, что при прочих равных условиях рt возрастает прямо пропорционально начальному давлению цикла ра. На практике повышение ра осуществляют за счет применения наддува. В бензиновых двигателях давление наддува ограничено возникновением детонации.
Среднее давление цикла повышается с увеличением количества подведенной теплоты (ростом λ = Тz/Тc ). Однако, если на максимальную температуру цикла Тz наложено ограничение, связанное, например, с требованием уменьшения выбросов двигателем оксидов азота NOх, то, как показывают расчеты, кривая среднего давления цикла в функции от степени сжатия проходит через максимум, рисунок 3. [4]
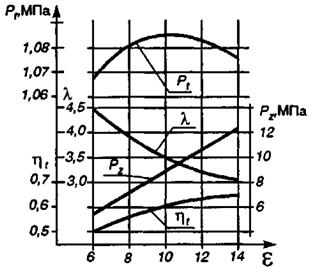
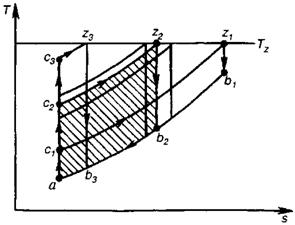
| Рисунок 3 – Зависимость показателей цикла Отто от степени сжатия при ограничении на максимальную температуру цикла (pa = 0,1 МПа, Та = 300К, Tz = 2700К, k=1,4) | Рисунок 4 – Совокупность циклов Отто с различными степенями сжатия при одинаковой максимальной температуре цикла |
Изменение конфигурации цикла с повышением степени сжатия при ограничении на максимальную температуру схематично показано на рисунке 4. Видно, что при повышении ε (переход от цикла ас1z1b1, к циклу ас3z3b3), работа цикла вначале увеличивается, а затем уменьшается. [4]
Циклы с подводом теплоты при постоянном объеме применяются в карбюраторных и инжекторных типах двигателей с использованием принудительного воспламенения от электрической искры. [2]
Цикл Дизеля
Двигатели, в основу работы которых положен термодинамический цикл с подводом теплоты при постоянном давлении, имеют ряд преимуществ по сравнению с двигателями, работающими по циклу с подводом теплоты при постоянном объеме. Они связаны с тем, что в двигателях, работающих по циклу Дизеля, осуществляется раздельное сжатие топлива и воздуха. Поэтому здесь можно достигать значительно более высоких степеней сжатия.
Воздух при высоких давлениях имеет настолько высокую температуру что подаваемое в цилиндр топливо самовоспламеняется без всяких специальных запальных приспособлений. Кроме того, раздельное сжатие воздуха и топлива позволяет использовать любое жидкое дешевое топливо – нефть, мазут, смолы и проч.
В двигателях, работающих по циклу Дизеля, воздух сжимается в цилиндре, а жидкое топливо распыляется сжатым воздухом от компрессора. Такая организация процесса сгорания позволяет применять существенно более высокие степени сжатия по сравнению с циклом Отто и исключить преждевременное самовоспламенение топлива. Постоянство давления при горении топлива обеспечивается соответствующей регулировкой топливной форсунки. Конструкция такого двигателя впервые была разработана немецким инженером Дизелем. [2]
Термодинамический цикл Дизеля показан на рисунке 5 и осуществляется следующим образом. Газообразное рабочее тело (воздух) с начальными параметрами pa, υa, Ta сжимается по адиабатеас, при этом происходит увеличение температуры и давления рабочего тела. В конце сжатия (точка с, ВМТ) через форсунку в цилиндр впрыскивается порция топлива в мелкораспыленном состоянии. Мелкие частицы топлива, соприкасаясь с нагретым сжатым воздухом, самовоспламеняются и процесс сгорания происходит при постоянном давлении. В изобарном процессе сzк рабочему телу подводится количество теплоты q1. Под большим давлением расширяющихся газов поршень перемещается к НМТ и передает воспринимаемое им усилие через шатун на коленчатый вал, заставляя его вращаться. Процесс zb – это изоэнтропное (адиабатное) расширение рабочего тела до первоначального объема. В точке b открывается выпускной клапан, под действием избыточного давления отработанные газы выходят из цилиндра. В изохорном процессе ba рабочее тело при постоянном объеме возвращается в исходное состояние с отводом от него теплоты в количестве q2. Полезная работа термодинамического цикла пропорциональна площади, ограниченной на диаграмме aczb. Рабочее тело совершает положительную работу lzbчасть которой в дальнейшем (при повторении цикла) затрачивается на осуществление процесса ас.
Ts-диаграмма используется для наглядного анализа количества подведенного q1 (площадь saaczbsb) и отведённого q2 (площадь saabsb) тепла и полезно использованного количества теплоты в цикле lЦ = q1 - q2 (площадь aczb).

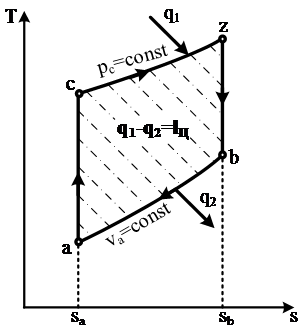
Рисунок 5 – Цикл Дизеля на pυ и Ts-диаграммах.
Цикл с подводом теплоты при р=const (термодинамический цикл Дизеля, с постепенным сгоранием) используется в двигателях высокого сжатия, например, на керосине. В этом цикле λ = 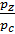 = 1. Кроме ε =
= 1. Кроме ε = 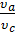 , параметрами этого цикла являются: ρ =
, параметрами этого цикла являются: ρ = 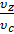 – степень предварительного расширения; δ =
– степень предварительного расширения; δ = 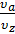 – степень последующего расширения.
– степень последующего расширения.
Параметры цикла связаны соотношением ε = ρδ.
Выразим объем, давление и температуру в характерных точках цикла (точки c, z и b) через характеристики цикла и его начальные параметры Та, υa,pa.
Точка с.
Удельный объём в точке сможно определить, используя определение степени сжатия:
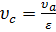 , , | (26) |
Процесс ac – адиабатный, тогда для него, используя уравнение адиабатного процесса,можно записать соотношение между параметрами:
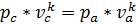 , , |
отсюда определяем давление в точке с:
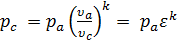 , , | (27) |
Аналогично, из уравнения адиабатного процесса ac:
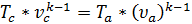 , , |
выразим температуру в точке с:
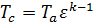 , , | (28) |
Точка z.
Зная степень предварительного расширения, можем определить удельный объем в точке z:
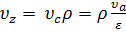 , , | (29) |
Процесс cz – изобарный, значит
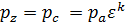 , , | (30) |
а отношение объемов равно отношению температур:
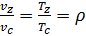 , , |
тогда, зная выражение температуры в предыдущей точке (28), получим температуру в точке z:
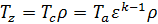 , , | (31) |
Точка b.
Процесс ba – изохорный, значит
| υb = υa., | (32) |
Зная, что процесс zb – адиабатный и выражение (29), можно записать
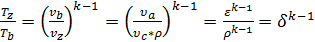 , , |
отсюда, используя (31) находим температуру в точке b:
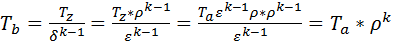 . . | (33) |
Так как процесс ba – изохорный, то отношение давлений равно отношению температур, т.е. получаем что:
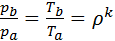 , , |
тогда давление в точке b равняется:
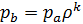 , , | (34) |
Таблица 2 – Расчет параметров рабочего тела в характерных точках цикла Дизеля.
| Параметры | Характерные точки цикла | |||
| a | c | z | b | |
| v | va | 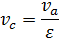 | 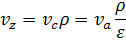 | 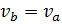 |
| p | pa | 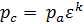 | 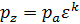 | 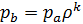 |
| T | Ta | 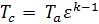 | 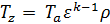 | 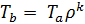 |
Используя полученные выражения температур в точках c (28), z(31), b(33), количество подведенной и отведенной теплоты можно выразить следующим образом:
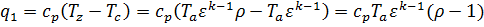 , , |
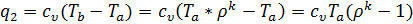 . . | (35) |
Подставляя эти результаты в ηt= 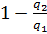 , получаем
, получаем
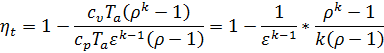 | (36) |
Тогда работу цикла используя выражение (36) можно определить как:
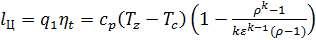 . . | (37) |
Подставляя (37) в выражение для определения среднего давления (6) в случае термодинамического цикла Дизеля, получим:
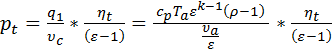 , , 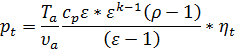 | (38) |
Используя уравнение Майера для идеального газа
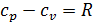 ,
,
и выражение для показателя адиабаты k
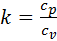 ,
,
выразим удельную теплоемкость при постоянном давлении 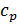 :
:
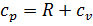 , , 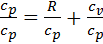 , , 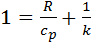 , cp = , cp = 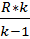 . . | (39) |
Подставляя выражение (39) в (38) среднее теоретическое давление в цикле Дизеля приводится к виду:
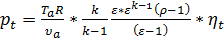 , , 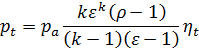 | (40) |
Таким образом, как и в случае цикла Отто, ηt и рt цикла Дизеля зависят от природы рабочего тела и степени сжатия, возрастая при повышении ε и показателя адиабаты k, уменьшаясь при росте ρ.
Величина ε в термодинамическом цикле с подводом теплоты при постоянном давлении выбирается таким образом, чтобы обеспечивать условия самовоспламенения топлива. Таким условиям в дизельных двигателях соответствует ε =14-20. [2]
Сравнение КПД циклов ДВС с подводом теплоты при p=const и υ=const при одинаковых максимальных давлениях или температурах, но при различных ε показывают, что КПД цикла Дизеля больше, чем у цикла Отто: ηtрДизель> ηtυОтто. [2]
В отличие от цикла Отто, в данном случае термический КПД зависит от тепловой нагрузки цикла, т.е. количества подведенной теплоты. С увеличением количества подведенной теплоты КДПηt, снижается. По условию организации отвода теплоты по изохоре ba величина ρ не может превышать значения ε. Несмотря на снижение термического КПД ηt увеличение количества подведенной теплоты приводит к росту среднего давления цикла.
Традиционно цикл с подводом теплоты при р=const считается термодинамическим циклом тихоходного дизеля, но могут использовать более тяжелое топливо, например, солярку. Однако при подборе подходящих значений ра и εэтот цикл может рассматриваться как модель цикла двигателя с искровым зажиганием при его работе на особо малых нагрузках и холостом ходу[4].
Цикл Саботэ-Тринклера
Одним из недостатков двигателей, в которых применяется цикл с подводом теплоты при постоянном давлении, является необходимость использования высокого давления, применяемого для подачи и распыления жидкого топлива. Это усложняет конструкцию и уменьшает экономичность двигателя, т.к. на повышение давления для подачи топлива затрачивается 6-10 % от общей мощности двигателя. [2, 3] В двигателях, работающих по термодинамическому циклу со смешанным подводом теплоты, жидкое топливо вводится в форкамеру при сравнительно невысоком давлении и распыляется струей сжатого воздуха, поступающего из основного цилиндра.
С целью упрощения конструкции и увеличения экономичности двигателя русский инженер Г.В. Тринклер разработал проект двигателя высокого сжатия. Этот двигатель лишен недостатков рассмотренных выше двух типов двигателей. Основное его отличие в том, что после сжатия воздуха в основной камере сгорания жидкое топливо с помощью топливного насоса под высоким давлением подается через форсунку VIII в головку цилиндра (форкамеру, VII), рисунок 6. В форкамере горючая смесь предварительно воспламеняется и горит вначале при постоянном объеме, а потом при постоянном давлении горение распространяется в цилиндр. [2]
Двигатели Тринклера чаще называют быстроходными или форкамерными дизелями.

Рисунок 6 – Схема поршневого ДВС, работающего по циклу
Триклера.
I – поршень, II – цилиндр, III – впускной клапан, IV – выпускной (выхлопной) клапан, V – впускной патрубок, VI – выпускной патрубок, VII – форкамера, VIII – форсунка, ВМТ – верхняя мертвая точка, НМТ – нижняя мертвая точка.
Смешанный термодинамический цикл (рисунок 7) относится к быстроходным дизелям. Минимальная величина степени сжатия в реальном дизеле определяется созданием условий надежного с
