Фотоэффект и его законы. Уравнение Эйнштейна для фотоэффекта. Фотоны. Дуализм волновых и корпускулярных свойств излучения.

Фотоэффект наз.испускание электронов веществом под действием света. Это было обнаружено, когда проводится опыт: проскальзывание искры между шариками облегчится, если один осветить ультрафиолетовыми лучами. Первым исследовал фотоэффект Столетов. Он установил что:1) наиболее эффективное действие оказывает ультрафиолетовое излучение;2)под действием света вещество теряет только отрицательные заряды;3)сила тока, возникающего под действием света, прямо пропорциональна его интенсивности.

Внутренний фотоэффект-это вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу. Вентильный фотоэффект- разновидность внутреннего возникновение э.д.с. при освещении контакта двух разных полупроводников или полупроводника и металла(при отсутствии внешнего эл.поля). 3 закона фотоэффекта:

1.Закон Столетова: при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода в единицу времени, пропорционально интенсивности света(сила фототока насыщения пропорциональна энергетической освещенности Е_е катода).

2.Максимальная начальная скорость( максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется его частотой ν.

3.Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота ν₀ света( зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.

hν=A+mv_max²/2-уравнение Эйнштейна для внешнего фотоэффекта (объясняет 2 и 3 законы). А –работа выхода`е.Максимальная кинетическая энергия фотоэлектрона возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), т.к. ни А, ни ν от интенсивности света не зависят(2 закон). Т.к. с уменьшением частоты света кинет.энергия фотоэлектрона уменьшается, то при некоторой 6.Корпускулярно-волновой дуализм материи. Гипотеза де Бройля. Опыты по дифракции микрочастиц.

Де Бройль выдвинул теорию о корп.-волн.дуализме материи, т.е. не только фотоны, но и электроны и любые другие частица материи наряду с корпускулярными обладают также волновыми свойствами. Каждые микрообъект связывают корпуск.характеристики –энергия Е и импульс р, а также волновые – частота ν и длина волны λ. Е=hν,p=h/λ. Т.о. любой частице обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемо по формуле де Бройля λ=h/p. Можно добавить то, что на частице вещества переносится связь между полной энергией частицы ε и частотой ν волн де Бройля:ε=hν , h-постоянная Планка=6,625·10^-34 Дж·с

Волна де Бройля – это волна, связанная с равномерным и прямолинейным движением частицы.

y=Acos(wt-kx) ü уравнения

y(x,t)=Aexp(-(wt-kx)) þ волны.

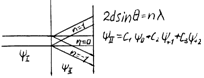
E=hw, p=hk, w=E/h, k=p/h. y(x,t)=Aexp(-i/h(Et-px)) – плоская волна де Бройля. Фазовая и групповая скорости волн де Бройля. Фазовая скорость – скорость распространения фазы . Et-px=const, Edt-pdx=0, <u>=dx/dt=E/p= =mc²/mu - средняя скорость волны. u_ф=c²/u, u_гр=dw/dk, E=hw, p=hk, E²-p²c²=m²₀c⁴; E=cÖ(p²+m²₀c⁴). u_гр=dw/dk=dE/dp= c2p/(2Ö(p²+m²₀c⁴))=pc2/cÖ(p²+m²₀c⁴)=pc²/mc²=p/m=mu/m=u. u_грu_ф=c². Дифракция микрочастиц. По идее де Бройля движение электрона или какой другой частицы связано с волновым процессом. l=2ph/p=2ph/mu (1); w=E/h. Гипотеза была подтверждена экспериментально в 1927 г. исследование отражения электронов от монокристалла никеля, принадлежащего к кубической системе. Узкий пучок моноэнергетических электронов направлялся на пов-ть монокристалла. Отраженные электроны улавливались цилиндрическим электродом, присоединенным к гальванометру. Интенсивность оценивалась по силе тока. Варьировалась скорость электронов и угол j. Рассеяние оказалось особенно интенсивным при угле, соответствующем отражению от атомных плоскостей, расстояние между которыми было известно из рентгенографических исследований. Вычисленная по формуле (1) длина волны примерно равна брэгговской длине волны, где 2dsinq=nl. Этот опыт подтвердил идею де Бройля. Томсон и Тартаковский независимо друг от друга получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Пучок электронов проходил через тонкую фольгу и попадал на фотопластину. Электрон при ударе о фотопластину оказывает на нее такое же действие как и фотон. Полученая таким же способом электрограмма золота сопоставлена с рентгенограммой алюминия. Сходство поразительно. Обнаружили, что дифф. Явления и у атомных и у молекулярных пучков, и длина волны l=2ph/p. Таким образом было доказано, что волновое сходство присуще отдельному электрону.

7. Волновая ф-ция, ее статический смысл и условие, которым она должна удовлетворять. Принцип суперпозиции в квантовой механике. Сдвижением частицы связывается волновой процесс, описываемый волновой ф-цией y(`r,t)= =y(x,y,z,t). y(`r,t)=y(`r)j(t). dp=|y|<sup>2</sup>dV=|y(`r,t)|²dxdydz – вероятность того, что частица находится в объеме dV, определяемая радиусом`r. Таким образом волновая ф-ция не имеет смысла, а квадрат модуля дает плотность вероятности нахождения частицы в пр-ве. Поскольку ф-ция не имеет смысла, то она может быть комплексной: ò|y|²dV=1 (от -¥ до ¥) – условие нормировки. y - нормированная, если удовлетворяется условие: |e^ia|²=e^ia, e^-ia=1. Требования к волновой ф-ции. w=|y|²=yy^*, ò|y|²dV=1. 1) Ф-ция должна быть квадратично интегрируема или конечна. 2) ф-ция должна быть однозначна. 3) непрерывность ф-ции вместе с первыми производными. Принцип суперпозиции. dw=|y|²dV, y=c₁y₁+c₂y₂. Если частица может находится в состоянии, описываемом волновой ф-цией y₁ и y₂, то она может находится и в состоянии y, являющейся линейной комбинацией этих состояний. y=c₁y₁+c₂y₂ (с₁ и с₂ могут быть комплексными), |c₁|² и |c₂|² дают вероятность того, что частица находится в состоянии 1 или в состоянии 2.