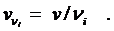Расчет химических равновесий. Тепловой закон Нернста

Прямой и простой расчет изобарных потенциалов реакций и К_Р возможен, если известны абсолютные энтропии всех участников реакции. Для реакций, протекающих при Т = const:

DG_T^o = DH_T^o – TDS_T^o

DH_T^o – теплота реакции при Р = const

DS_T^o – изменение S при превращении чистых исходных веществ, взятых в стандартном состоянии при Р = 1 атм, в конечные вещества в том же состоянии:

DS^o = ån_iS_i^o

Если для данной Т известны теплота реакции DН^о и энтропии S_i^o всех участников реакции, то расчет DG^o – элементарная арифметическая операция.

Если известны C_P = f(T), можно вычислить DН^о при данной Т по уравнению Кирхгоффа и S каждого участника по уравнению:

S_T = + + + +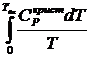

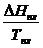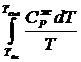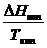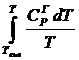
а затем найти DG^o.

Т.о., изложенный метод расчета химических равновесий базируется на постулате Планка. Однако для обоснования метода расчета достаточно утверждение, что изменение энтропии для всех процессов (в том числе и химических реакций), происходящих при Т = 0 с участием только кристаллических чистых веществ, равно нулю. Действительно:

S = S_o +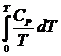

Изменение S при химической реакции составляет:

DS = DS_o +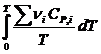

Приняв DS_o = 0, получим: DS = 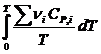= ån_i ,

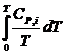т.е. возможность вычислить DS, используя те же табличные величины стандартных энтропий.

Уравнение DS_o = 0 является выражением теплового закона Нернста, который был исторически первой формой третьего закона термодинамики, высказанной Нернстом в 1906 г.

Изложенный метод расчета химических равновесий называется методом абсолютных энтропий и является общим для реакций в любых системах. Он позволяет использовать эмпирические уравнения.

DG_T^o = DH_T^o – TDS_T^o

DH_T^o = DН^о₂₉₈ + 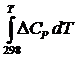; (DН^о₂₉₈)_x = ån(DН^о_{f, 298})_{конеч.в-в} - ån(DН^о_{f, 298})_нач.в-в

DS_T^o = DS^o₂₉₈ +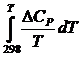

DG_T^o = DН^о₂₉₈ + 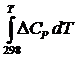– TDS^o₂₉₈ – T 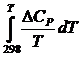– уравнение для точного расчета изобарного потенциала реакции; надо знать: DS^o₂₉₈ и С_Р(Т). Расчет точного значения DG_T^o по этому уравнению при высоких Т часто невозможен из-за отсутствия соответствующих экспериментальных данных. В таких случаях возможно применение приближенных методов расчета изобарных потенциалов.

ПЕРВОЕ ПРИБЛИЖЕНИЕ УЛИХА : DС_Р = 0 – применяется, когда С_Р некоторых участников реакции совершенно неизвестны. Получаем:

DG_T^o = DH^о₂₉₈ – TDS^о₂₉₈

– в пределах Т не более 600 К дает удовлетворительные результаты.

ВТОРОЕ ПРИБЛИЖЕНИЕ УЛИХА : DС_Р = const – применяется, если числовые значения С_Р участников реакции известны при комнатной Т.

DG_T^o = DH^о₂₉₈ – TDS^о₂₉₈ + DС_Р(Т – 298) – ТDС_Р ln =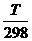

= DH^о₂₉₈ – TDS^о₂₉₈ – DC_PT 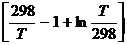= DH^о₂₉₈ – TDS^о₂₉₈ – M_oDC_PT

Значения М_о при различных Т сведены в таблицу.

МЕТОД ТЕМКИНА – ШВАРЦМАНА расчета DG^o :

DC_P = D a + D bT + D cT² + … + D nTⁿ

DG_T^o = DH^о₂₉₈ – TDS^о₂₉₈ – T× (D aM_o + D bM₁ + D cM₂ + … + D nM_n)

M_o = 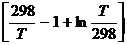; M₁ =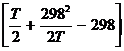

M_n = + –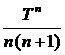

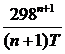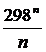
Выражение для M_n справедливо и для n = – 2. Коэффициенты М_о, М₁ … уравнения зависят только от Т; они сведены в таблицу для разных Т.

Отсутствие значений DS^о₂₉₈ многих веществ (огромного большинства из них) приводит к необходимости пользоваться некоторыми приближенными закономерностями для их подсчета. Известно значительное число таких закономерностей, предложенных разными авторами, охватывающих большие или меньшие группы соединений и дающих результаты разной степени точности.

Основной постулат химической кинетики. Скорость химической реакции, скорость реакции средняя и истинная. Кинетическая классификация реакций, различие понятий «порядок реакции» и «молекулярность реакции», понятие об элементарной реакции. Необратимые реакции первого, второго, n-го и нулевого порядка.

В общем виде химическую реакцию можно записать следующим образом:

n₁ А₁ + n₂ А₂ + ... + n_n A_n = n₁¢A₁¢ + n₂¢A₂¢ + ... + n_n¢A_n¢ .

Скоростью химической реакции называется количество молекул данного сорта, реагирующих в единицу времени в единице объёма. Для определения скорости химической реакции достаточно знать изменение во времени количества одного из участвующих в реакции веществ (исходного или конечного), так как изменение количества всех остальных веществ можно определить из уравнения реакции.

Химические реакции редко протекают в одну стадию, так, как их принято записывать. Запись уравнения реакции можно рассматривать как символическое выражение материального баланса (закона сохранения вещества). В действительности подавляющая часть химических реакций протекает через ряд промежуточных стадий, и в большинстве случаев детальный механизм протекания реакции нам неизвестен из-за больших трудностей выявления промежуточных продуктов. Скорость суммарной реакции определяется скоростью наиболее медленной стадии, которая называется лимитирующей.

Еще в самом начале исследований по химической кинетике было сделано физически очевидное предположение, что реагируют только те молекулы, которые сталкиваются. Как известно, число столкновений прямо пропорционально числу молекул, поэтому скорость реакции должна быть пропорциональна концентрации реагирующих веществ. В общем случае можно принять, что скорость химической реакции прямо пропорциональна концентрациям реагирующих веществ в некоторых степенях:

v = k 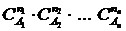, [v] = моль/(м³×с) или молекул/(м³×с) ;

k - константа скорости химической реакции, k зависит от природы реакции и является функцией температуры;

n_i - порядок реакции по данному веществу; в общем случае порядки реакции по веществам никак не связаны со стехиометрическими коэффициентами n_i этих веществ в уравнении реакции, и только в тех случаях, когда реакция протекает в одну стадию, порядок реакции n_i по данному веществу совпадает со стехиометрическим коэффициентом n_i данного вещества в химическом уравнении.

Вышеприведенное выражение называют основным постулатом химической кинетики.

Физический смысл коэффициента k : v = k , если 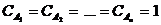, то есть константа скорости химической реакции есть скорость реакции при условии, что концентрации реагирующих веществ равны 1; k иногда называют удельной скоростью химической реакции. Размерность константы скорости зависит от порядка реакции.

Скорость реакции является функцией времени, так как количества реагирующих веществ меняются во времени. Введем понятие средней скорости реакци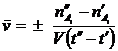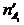и:

,

и 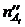- число молей одного из веществ в начальный t¢ и конечный t¢¢ моменты времени; V - объем системы. Знак «-» в выражении стоит тогда, когда мы следим за ходом реакции по изменению количества одного из исходных веществ, поскольку в этом случае 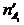> 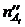, а скорость реакции может быть только положительной величиной. Знак «+» используют, если скорость реакции определяют по ее продукту.

Если t¢¢ - t¢ ® 0 , то получим истинную скорость v реакции (скорость реакции в данный момент времени):

v = ± .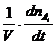

Если V = const, то v = ± .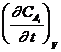

Этим уравнением удобно пользоваться при рассмотрении реакций в растворах, так как изменением объема раствора в результате реакции во многих случаях можно пренебречь.

Скорость реакции зависит от природы реагирующих веществ, их концентрации, температуры и наличия катализатора.

Следует иметь в виду, что при вышеприведенном определении скорости химической реакции (число молекул, реагирующих в единицу времени в единице объема) числовое значение величины скорости реакции будет зависеть от того, какое вещество из участвующих в реакции мы выбрали, чтобы следить за ее скоростью, так как стехиометрические коэффициенты разных участников реакции могут отличаться друг от друга. Например, в реакции синтеза бромоводорода

Н₂ + Br₂ = 2HBr

за одно и то же время образуется в 2 раза большее число молей HBr, чем прореагирует молей Н₂ и Br₂ , и, следовательно, скорость реакции, определенная по бромоводороду, будет в 2 раза выше, чем скорость, определенная по водороду либо по брому:

.

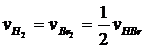Чтобы устранить эту неопределенность, скорость реакции рассчитывают на единицу стехиометрического коэффициента, и тогда ее величина не зависит от того, по какому веществу ее определяют:

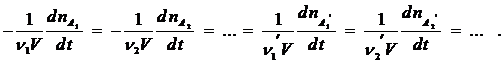
В общем виде можно записать:

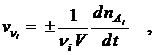где