Критериальное уравнение осаждения.
скорость осаждения 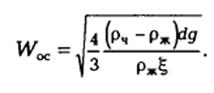
Значение коэф-та сопротивления ξ может быть определено по одной из зав-тей ξ от критерия Рейнольдса при движении шарообразных частиц диаметром d. Существует 3 различных режима движения, каждому из которых соответствует определенный характер зависимости ξ от Re:
Ламинарный режим приблизительно при Re<2
ξ = 24/Re =>(Re~w)
Переходный режим при Re=2-500
ξ =18,5/Re0,5 =>(Re~w1,4)
Турбулентный режим при ~2·105>Re>~500
ξ =0,44=const =>(Re~w2)
При подстановке в уравнение выражения (1.2а) для ламинарной области находим формулу wос=d2g(ρT -ρ)/18µ где µ–вязкость среды (1.3а)
В случае переходной области 2 < Re < 500 после подстановки в уравнение (1.1) выражения (1.2б) для ξ и некоторых преобразований получим
wос=0,78d0,43g(ρT -ρ)0,715/(ρ0,285µ0,43) (1.3б)
Аналогично для турбулентной области (при Re> 500), согласно выражению (1.2в), подставив ξ = 0,44 в уравнение (1.1)находим wос=5,46√4(ρT -ρ)/ρ (1.3в)
Для того чтобы выбрать расчетное ур-ние, соответствующее данной области осаждения, т. е, одно из уравнений(1.3а), (1.3б), (1.3в) необходимо предварительно знать значение критерия Re, в который входит искомая скорость осаждения wос. Поэтому расчет Woc по приведенным выше уравнениям возможен только методом последовательных приближений. Допуская, что осаждение происходит в опред. области, н-р ламинарной, рассчитывают по соответствующему уравнению Woc и по этому значению вычисляют Re. Затем проверяют, лежит ли найденное значение Re в пределах, отвечающих принятой области осаждения. В случае несовпадения расчет повторяют до получения сходимых результатов.
Вследствие трудоемкости метода последовательных приближений более удобно для определения Woc пользоваться другим методом; предложенным П. В. Лященко. Этот метод основан на преобразовании уравнения (1.1) путем подстановки в него скорости осаждения, выраженной через Re, и возведения обеих частей уравнения в квадрат,Откуда Re2ξ =(4/3)d3ρ2g (ρT -ρ)/ρµ2
Выражение в правой части этого уравнения принципиально не отличается от выражения для критерия Аг: Ar=d3ρ2g (ρT -ρ)/ρµ2
В данном случае за определяющий линейный размер принят диаметр частицы, а за масштаб разности плотностей частицы и среды - плотность среды, в которой происходит осаждение.
В критерий Архимеда искомая скорость осаждения не входит. Он состоит из величин, к-ые обычно либо заданы, либо могут быть заранее определены.
Таким образом Re2ξ=(4/3)Ar (1.4)
Подставив в это Обобщенное уравнение критические (граничные) значения критерия Re, отвечающие переходу одной области осаждения в другyю, можно найти соответствующие критические значения критерия Ar.
Для области действия Зaкона Стокса (Re < 2) при подстановке выражения ξ, согласно зав-ти (1.2а), в уравнение (1.4) получим Re=Ar/18 (1.4a)
Верхнее предельное, или критическое, значение критерия Архимеда для этой области Arкр.1= 18*2 = 36
Следовательно, 'существование ламинарного режима осаждения соответствует условию Аг<или=36
Для переходной 06ласти, где 2 < Re < 500, подставляем значениеξ, согласно зависимости (1.2б), в уравнение (1.4). Тогда Re=0,152Ar0,715 (1.4б)
При подстановке в уравнение (1.5б) критического значения Re = 500 находят верхнее предельное значение Аг для переходной области
Arкр.2= 83 000
Таким образом, переходная обласrь осаждения соответствует изменению критерия Аг, в пределах 36 <Аг <83 000.
Для турбулентной области, где Аг> 83 000, зависимость между Re и Аг можно найти, подставив ξ= 0,44, в соответствии с выражением (1.2в), в уравнение (1.4):
__
Re=1,74√Ar (1.4в)
Таким образом, рассчитав критерий Аг, определяют по его значению область, в которой происходит осаждение. Вычисляют, пользуясь одним из уравнений(1.4a), (1.4б), (1.4в)
отвечающим этой области, значение Re и находят по нему скорость осаждения
wос=µRe/dρ
Зная область осаждения, можно также рассчитать скорость осаждения по одному из уравнений (1.3а), (1.3б), (1.3в). Для расчетов может быть использована и единая интерполяционная зависимость, связывающая критерии Re и Аг для всех режимов осаждения:
__
Re = Ar/(18+0,575√Ar) (1.5)
При малых значениях Аг вторым слагаемым в знаменателе можно пренебречь, и уравнение (1.5) превращается в уравнение (1.4а), соответствующее области действия закона Стокса; при больших же значениях Ar пренебречь можно уже первым слагаемым в знаменателе, и уравнение (1.5) превращается в уравнение (1.4в), отвечающее турбулентной области.
Скорость осаждения wос частии нешарообразной формы меньше, чем скорость осаждения шарообразных частиц. Чтобы ее рассчитать, значение скорости осаждения Woc для· шарообразных частиц необходимо умножить на поправочный коэффициент φ, называемый коэффициентом формы
W’ос=φWос
Коэффициент φ<1, и его значения определяют опытным путем. Так, для частиц округлой формы φ~ 0,77, для угловатых частиц φ~ 0,66, для продолговатых частиц φ~ 0,58 и для пластинчатых частиц φ~ 0,43.
Кроме того, при расчете скорости осаждения частиц нешарообразной формы в соответствующие уравнения для определения скорости следует подставлять диаметр эквивалентного шара d, равный диаметру шара, имеющего такой же объем, что и данное тело. Если объем тела V, его масса m, а плотность ρT, то значение d может быть найденоиз соотношения
V=m/ ρT=πd2/6
Приведенный расчет W’ос и Wос относится к скорости с в о б о д н о г о о с а ж д е н и я, при котором осаждающиеся частицы практически не оказывают влияния на движение друг друга. При значительной концентрации твердых частиц в среде происходит стесненное осаждение, скорость которого меньше, чем свободного, вследствие трения и соударений между частицами.
