Градиент потенциальной энергии. Связь силы и потенциальной энергии. Движение частицы в потенциальном поле.
Градиент — вектор, показывающий направление наискорейшего возрастания некоторой величины 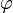 , значение которой меняется от одной точки пространства к другой (скалярного поля).
, значение которой меняется от одной точки пространства к другой (скалярного поля).
Градиент потенциальной энергии– первая производная потенциальной энергии молекулярной системы по ядерным координатам. Точки ППЭ, в которых градиент энергии равен нулю, отвечают глобальному или локальному минимуму или переходному состоянию конфигурации молекулярной системы.
Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы F, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии Wп. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.
Дальше много вычислений, в конце получаем: 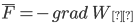
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
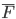 =
= 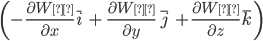
Сила равна градиенту потенциальной энергии, взятого с обратным знаком:
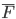 =
= 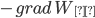
Причиной движения материальной частицы является потенциальное поле, то мы вынуждены признать, что под воздействием этого поля частица должна двигаться ускоренно.
| ||||||||||||||||||||||||||
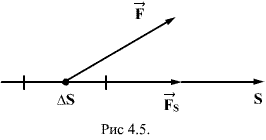
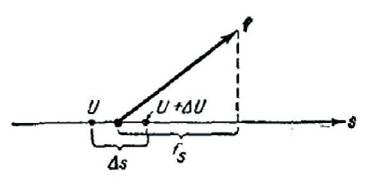
| Каждой точке потенциального поля соответствует одной стороны, некоторое значение вектора силы f, действующей на тело, с другой стороны, некоторое значение потенциальной энергии тела U. Следовательно, между силой и потенциальной энергией должна существовать определенная связь. Для установления этой связи вычислим элементарную работу, ΔA совершаемую силами поля при малом перемещении тела Δs, происходящем вдоль произвольно выбранного направления в пространстве, которое мы обозначим буквой s (рис. 66), Эта работа равна:
Рис.66
где fs — проекция силы f на направление s. Поскольку в данном случае работа совершается за счет запаса потенциальной энергии, она равна убыли потенциальной энергии — ΔU на отрезке Δs оси s:
Сопоставляя (28.1) и (28.2), получаем:
откуда:
Выражение (28.3) даст среднее значение fs на отрезке Δs. Чтобы получить значение fs в данной точке, нужно произвести предельный переход:
Поскольку U может изменяться не только при перемещении вдоль оси s, но также и при перемещениях вдоль других направлений, предел в формуле (28.4) представляет собой так называемую частную производную от U по s:
Соотношение (28.5) справедливо для любого направления в пространстве, в частности, и для направления декартовых координатных осей x, y, z:
Формулы (28.6) определяют проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы. В соответствии с (2.8)
В математике вектор
где a — скалярная функция x, y, z, называется градиентом этого скаляра и обозначается символом grada. Следовательно, сила равна градиенту потенциальной энергии, взятому с обратным знаком
Пример. Возьмем в качестве примера поле сил тяжести. Ось
Проекция силы на оси согласно (28.6) равны:
Рис.67 откуда следует, что сила равна mg и направлена в сторону, противоположную направлению z, т. е. вниз по вертикали. 4.3. Консервативные силы. Условие потенциальности силового поля
Силу
Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина
Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным. 4.8. Связь между потенциальной энергией и силой Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы
Для установления этой связи вычислим элементарную работу
где Поскольку в данном случае работа совершается за счет запаса потенциальной энергии
Из двух последних выражений получаем
Откуда
Последнее выражение дает среднее значение получить значение
Так как
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
в математике вектор где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом
Рассмотрим систему, состоящую из многих материальных точек. Если задано положение каждой материальной точки, то этим определено и положение всей системы или ее конфигурация. Если силы, действующие на материальные точки системы, зависят только от конфигурации системы (т.е. только от координат материальных точек) и сумма работ этих сил при перемещении системы из одного положения в другое не зависит от пути перехода, а определяется только начальной и конечной конфигурациями системы, то такие силы называются консервативными. В этом случае для системы материальных точек также можно ввести понятие потенциальной энергии системы, обладающей свойством (7): где Связь между силой, действующей на тело в данной точке поля, и его потенциальной энергией определяется по следующим формулам:
или где
Часто формулу (9) записывают также в виде |

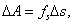
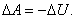
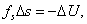
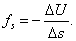
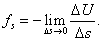
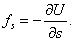
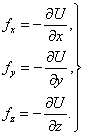
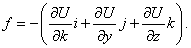
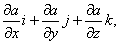
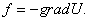
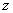 направим по вертикали вверх (рис. 67). При таком выборе координатных осей потенциальная энергия будет иметь вид
направим по вертикали вверх (рис. 67). При таком выборе координатных осей потенциальная энергия будет иметь вид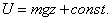
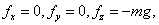
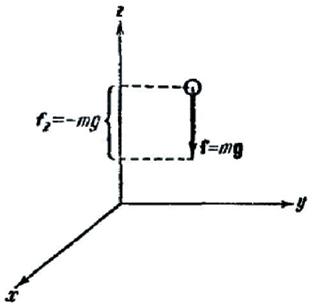
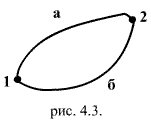
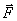 , действующую на материальную точку, называют консервативной или потенциальной, если работа
, действующую на материальную точку, называют консервативной или потенциальной, если работа 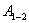 , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:
, совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло: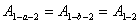
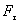 меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории
меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории 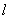 , например
, например  , работа консервативной силы равна нулю.
, работа консервативной силы равна нулю.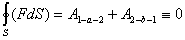
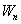 . Следовательно, между силой и потенциальной энергией должна существовать определенная связь.
. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.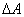 , совершаемую силами поля при малом перемещении
, совершаемую силами поля при малом перемещении 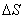 тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой
тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой 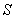 . Эта работа равна
. Эта работа равна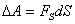
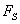 - проекция силы
- проекция силы 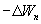 на отрезке оси
на отрезке оси 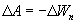
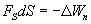
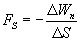
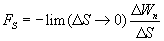
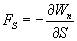
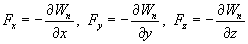
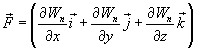
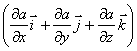 ,
,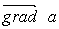 .Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком
.Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком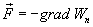
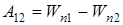 , (8)
, (8)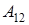 - полная работа консервативных сил, действующих на материальные точки системы при переходе ее из конфигурации 1 в конфигурацию 2;
- полная работа консервативных сил, действующих на материальные точки системы при переходе ее из конфигурации 1 в конфигурацию 2; 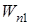 и
и 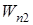 - значения потенциальной энергии системы в этих конфигурациях.
- значения потенциальной энергии системы в этих конфигурациях.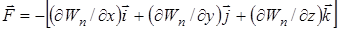 (9)
(9)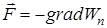 , (10)
, (10)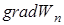 – называется градиентом скалярной функции
– называется градиентом скалярной функции 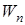 ;
; 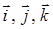 – единичные векторы координатных осей;
– единичные векторы координатных осей;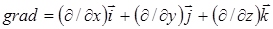 . (11)
. (11)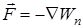 , где
, где 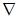 – оператор набла, определяемый по формуле (11).
– оператор набла, определяемый по формуле (11).