Вращательное движение твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение.
Абсолютно твердое тело –тело взаимное расположение частей которого во время движения не меняется.
Поступательное движение твёрдого тела - это такое его движение, при котором любая прямая, жёстко связанная с телом, перемещается, оставаясь параллельной своему первоначальному направлению.
При поступательном движении твёрдого тела все его точки движутся одинаково за малое время dt, радиус-вектор этих точек изменяется на одну и ту же величину. Соответственно в каждый момент времени скорости всех его точек одинаковы и равны. Поэтому кинематика рассматриваемого поступательного движения твёрдого тела сводится к изучению движения любого из его точек. Обычно рассматривают движение центра инерции твёрдого тела, свободно двигающегося в пространстве.
Вращательное движение твёрдого тела - это такое движение, при котором все его точки движущиеся по окружностям, центры которых находятся вне пределов тела. Прямая называется осью вращения тела.
Угловая скорость– векторная величина, характеризующая быстроту вращения тела; отношение угла поворота ко времени, за которое этот поворот произошёл; вектор, определяемый первой производной угла поворота тела по времени. Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта. ω=φ/t=2π/T=2πn, где T – период вращения, n – частота вращения. ω=limΔt→0Δφ/Δt=dφ/dt.
Угловое ускорение – вектор, определяемый первой производной угловой скорости по времени. При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. Вторая производная угла поворота по времени. При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору φ, при замедленном – противонаправлен ему. ε=dω/dt.
Если dω/dt> 0, то ε↑↑ω
Если dω/dt< 0, то ε ↑↓ω
4. Принцип инерции (первый закон Ньютона). Инерциальные системы отсчета. Принцип относительности.
Первый закон Ньютона (закон инерции): всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют законом инерции.
Первый закон Ньютона утверждает существование инерциальных систем отсчёта.
Инерциальная система отсчёта – это система отсчёта, относительно которой свободная материальная точка неподверженная воздействию других тел, движется равномерно прямолинейно; это такая система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы.
Принцип относительности - фундаментальный физический закон, согласно которому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе в состоянии равномерного прямолинейного движения. Состояния движения или покоя определяются по отношению к произвольно выбранной инерциальной системе отсчета. Принцип относительности лежит в основе специальной теории относительности Эйнштейна.
Принцип относительности (Галилея): никакие опыты (механические, электрические, оптические), проведённые внутри данной инерциальной системы отсчёта, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчёта к другой.
5. Преобразования Галилея.
Принцип относительности (Галилея): никакие опыты (механические, электрические, оптические), проведённые внутри данной инерциальной системы отсчёта, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчёта к другой.
Рассмотрим две системы отсчета: инерциальную систему К (с координатами x,y,z), которую условно будем считать неподвижной и систему К’ (с координатами x’,y’,z’), движущуюся относительно К равномерно и прямолинейно со скоростью U (U = const). Найдем связь между координатами произвольной точки А в обеих системах. r = r’+r0=r’+Ut. (1.)
Уравнение (1.) можно записать в проекциях на оси координат:
x=x’+Uxt;
y=y’+Uyt; (2.)
z=z’+Uzt; Уравнение (1.) и (2.) носят название преобразований координат Галилея.
Связь между потенциальной энергией и силой
Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы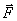 
, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии 
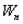. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.
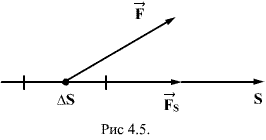
Для установления этой связи вычислим элементарную работу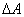 
, совершаемую силами поля при малом перемещении 
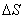тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой 
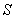. Эта работа равна
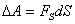
где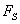 
- проекция силы 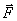на направление .
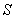Поскольку в данном случае работа совершается за счет запаса потенциальной энергии 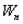, она равна убыли потенциальной энергии 
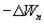на отрезке оси :
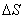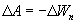
Из двух последних выражений получаем
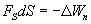
Откуда
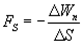
Последнее выражение дает среднее значение 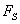на отрезке 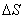. Чтобы
получить значение 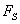в точке нужно произвести предельный переход:
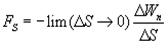
Так как 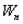может изменяться не только при перемещении вдоль оси 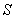, но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от 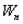по :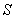
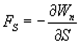
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
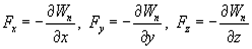
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
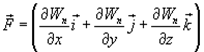
в математике вектор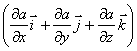 
,
где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом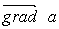 
. Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком
 |
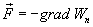