Стационарный поток. Поле скоростей. Линии и трубки тока. Уравнение неразрывности. Уравнение Бернулли.
Гидродинамика
(Элементы механики сплошных сред)
Линии и трубки тока. Теорема о неразрывности струи
Гидродинамика -раздел механики сплошных сред, в котором изучается движение несжимаемых жидкостей и взаимодействие несжимаемых жидкостей с твёрдыми телами. Рассмотрим движение несжимаемой жидкости. Состояние движения жидкости можно определить, указав для каждой точки пространства вектор скорости 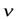 , как функцию времени
, как функцию времени 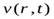 .Совокупность векторов
.Совокупность векторов 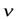 , заданных для всех точек пространства, образует так называемое поле вектора скорости
, заданных для всех точек пространства, образует так называемое поле вектора скорости 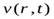 .
.
Стационарное течение – это установившееся движение жидкости, при котором вектор скорости в каждой точке пространства остаётся постоянным, т.е.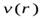 .
.
Линии тока-это линии, проведённые в движущейся жидкости так, что касательные к ним в каждой точке совпадают по направлению с вектором скорости .Густота линий тока пропорциональна величине скорости в данном месте.
.Густота линий тока пропорциональна величине скорости в данном месте.
Трубка тока–это часть жидкости, ограниченная линиями тока.Частицы жидкости при своём движении не пересекают стенок трубки тока.
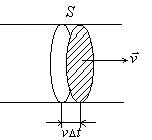
Возьмем несжимаемую жидкость и рассмотрим в ней трубку тока. Объём жидкости, прошедшей через поперечное сечение S за время Dt, равен SvDt.
ТогдаQ = Sv -поток жидкости, т.е. объём жидкости, прошедшей через поперечное сечение S за единицу времени.
Если жидкость несжимаема, то объем жидкости между сечениями S1 и S2 будет оставаться неизменным, и тогда S1v1= S2v2 . Это справедливо для любой пары S1 и S2 , и мы получаем
Sv = const – теорема о неразрывности струи:
Для несжимаемой жидкости величина потока жидкости Sv в любом сечении одной и той же трубки тока должна быть одинаковой.
Истечение жидкости из отверстия
Рассмотрим истечение жидкости из небольшого отверстия в широком открытом сосуде. Выделим в жидкости трубку тока, имеющую своим сечением с одной стороны открытую поверхность, а с другой стороны – отверстие, через которое вытекает жидкость. P1 = P2 – давления в обоих сечениях равны атмосферному. Скорость перемещения открытой поверхности в широком сосуде положим, равна нулю. Тогда:
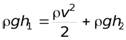
где v – скорость течения из отверстия. Отсюда:
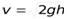 - формула Торричелли, где h = h1 - h2
- формула Торричелли, где h = h1 - h2
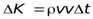 -импульс силы.
-импульс силы.
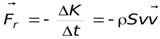 - реакция вытекающей струи.
- реакция вытекающей струи.
Навигация
Главная
Учебные материалы
Оглавление
Оглавление нижнее
Вверх
Вниз
Оглавление
Медицинская и биологическая физика. Курс лекций с задачами : учеб. пособие / В.Н. Федорова, Е.В. Фаустов. - 2008. - 592 с.
·ПРЕДИСЛОВИЕ
·ПЛАН ЛЕКЦИЙ
·ЛЕКЦИЯ 1 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
·ЛЕКЦИЯ 2 МЕХАНИЧЕСКИЕ ВОЛНЫ
·ЛЕКЦИЯ 3 АКУСТИКА. ЗВУК
·ЛЕКЦИЯ 4 НЕКОТОРЫЕ ВОПРОСЫ ФИЗИКИ СЛУХА
·ЛЕКЦИЯ 5 УЛЬТРАЗВУК И ИНФРАЗВУК
·ЛЕКЦИЯ 6 МЕХАНИЧЕСКИЕ СВОЙСТВА ТКАНЕЙ
·ЛЕКЦИЯ 7 УРАВНЕНИЕ БЕРНУЛЛИ И ЕГО СЛЕДСТВИЯ
·ЛЕКЦИЯ 8 ВЯЗКОСТЬ ЖИДКОСТИ
·ЛЕКЦИЯ 9 ФИЗИЧЕСКИЕ ОСНОВЫ ГЕМОДИНАМИКИ
·ЛЕКЦИЯ 10 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
·ЛЕКЦИЯ 11 ФИЗИЧЕСКИЕ ПРОЦЕССЫ В МЕМБРАНАХ
·ЛЕКЦИЯ 12 БИОЭЛЕКТРИЧЕСКИЕ ПОТЕНЦИАЛЫ
·ЛЕКЦИЯ 13 ДИПОЛЬ. ФИЗИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОГРАФИИ
·ЛЕКЦИЯ 14 ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
·ЛЕКЦИЯ 15 ПЕРЕМЕННЫЙ ТОК
·ЛЕКЦИЯ 16 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
·ЛЕКЦИЯ 17 ФИЗИЧЕСКИЕ ПРОЦЕССЫ, ПРОИСХОДЯЩИЕ В ТКАНЯХ ОРГАНИЗМА ПОД ВОЗДЕЙСТВИЕМ ТОКОВ И ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
·ЛЕКЦИЯ 18 НЕКОТОРЫЕ ВОПРОСЫ МЕДИЦИНСКОЙ ЭЛЕКТРОНИКИ
·ЛЕКЦИЯ 19 УСИЛИТЕЛИ. ГЕНЕРАТОРЫ
·ЛЕКЦИЯ 20 ИНТЕРФЕРЕНЦИЯ СВЕТА
·ЛЕКЦИЯ 21 ДИФРАКЦИЯ СВЕТА
·ЛЕКЦИЯ 22 ПОЛЯРИЗАЦИЯ СВЕТА
·ЛЕКЦИЯ 23 ГЕОМЕТРИЧЕСКАЯ ОПТИКА
·ЛЕКЦИЯ 24 ГЛАЗ И ЕГО ФУНКЦИИ
·ЛЕКЦИЯ 25 МИКРОСКОПИЯ
·ЛЕКЦИЯ 26 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
·ЛЕКЦИЯ 27 ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ КВАНТОВОЙ МЕХАНИКИ.
·ЛЕКЦИЯ 28 ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ
·ЛЕКЦИЯ 29 ЛЮМИНЕСЦЕНЦИЯ
·ЛЕКЦИЯ 30 ФОТОБИОЛОГИЧЕСКИЕ ПРОЦЕССЫ
·ЛЕКЦИЯ 31 ЛАЗЕРЫ. ЛАЗЕРНОЕ ИЗЛУЧЕНИЕ
·ЛЕКЦИЯ 32 РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ
·ЛЕКЦИЯ 33 РАДИОАКТИВНОСТЬ
·ЛЕКЦИЯ 34 ДОЗИМЕТРИЯ
·РЕКОМЕНДУЕМАЯ НАУЧНАЯ И НАУЧНО-ПОПУЛЯРНАЯ ЛИТЕРАТУРА
Категории
·Акушерство и Гинекология
·Анатомия
·Безопасность жизнедеятельности и медицина катастроф
·Биология
·Внутренние болезни
·Гематология
·Гигиена
·Гистология, эмбриология и цитология
·Госпитальная терапия
·Госпитальная хирургия
·Гуманитарные науки
·Дерматовенерология
·Детская хирургия
·Иностранные языки
·Инфекционные болезни
·Микробиология и вирусология
·Неврология и нейрохирургия
·Нормальная физиология
·Общая хирургия
·Общественное здоровье и здравоохранение
·Онкология
·Офтальмология
·Патологическая анатомия
·Патофизиология
·Педиатрия
·Поликлиническая терапия
·Пропедевтика внутренних болезней
·Пропедевтика детских болезней
·Психиатрия
·Психология и педагогика
·Социальные науки
·Стоматология
·Судебная медицина
·Топографическая анатомия и оперативная хирургия
·Травматология и ортопедия
·Факультетская терапия
·Факультетская хирургия
·Фармакология
·Физическая культура
·Физика и медицинская информатика
·Фтизиатрия
·Химия
·Экономика и управление
·Разное
·Библиотека
·Обмен файлами
Начало формы
Конец формы Интернет Картинка
| |||||||||||
Яндекс.Директ | |||||||||||
Оглавление
Медицинская и биологическая физика. Курс лекций с задачами : учеб. пособие / В.Н. Федорова, Е.В. Фаустов. - 2008. - 592 с.
·ПРЕДИСЛОВИЕ
·ПЛАН ЛЕКЦИЙ
·ЛЕКЦИЯ 1 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
·ЛЕКЦИЯ 2 МЕХАНИЧЕСКИЕ ВОЛНЫ
·ЛЕКЦИЯ 3 АКУСТИКА. ЗВУК
·ЛЕКЦИЯ 4 НЕКОТОРЫЕ ВОПРОСЫ ФИЗИКИ СЛУХА
·ЛЕКЦИЯ 5 УЛЬТРАЗВУК И ИНФРАЗВУК
·ЛЕКЦИЯ 6 МЕХАНИЧЕСКИЕ СВОЙСТВА ТКАНЕЙ
·ЛЕКЦИЯ 7 УРАВНЕНИЕ БЕРНУЛЛИ И ЕГО СЛЕДСТВИЯ
·ЛЕКЦИЯ 8 ВЯЗКОСТЬ ЖИДКОСТИ
·ЛЕКЦИЯ 9 ФИЗИЧЕСКИЕ ОСНОВЫ ГЕМОДИНАМИКИ
·ЛЕКЦИЯ 10 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
·ЛЕКЦИЯ 11 ФИЗИЧЕСКИЕ ПРОЦЕССЫ В МЕМБРАНАХ
·ЛЕКЦИЯ 12 БИОЭЛЕКТРИЧЕСКИЕ ПОТЕНЦИАЛЫ
·ЛЕКЦИЯ 13 ДИПОЛЬ. ФИЗИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОГРАФИИ
·ЛЕКЦИЯ 14 ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
·ЛЕКЦИЯ 15 ПЕРЕМЕННЫЙ ТОК
·ЛЕКЦИЯ 16 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
·ЛЕКЦИЯ 17 ФИЗИЧЕСКИЕ ПРОЦЕССЫ, ПРОИСХОДЯЩИЕ В ТКАНЯХ ОРГАНИЗМА ПОД ВОЗДЕЙСТВИЕМ ТОКОВ И ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
·ЛЕКЦИЯ 18 НЕКОТОРЫЕ ВОПРОСЫ МЕДИЦИНСКОЙ ЭЛЕКТРОНИКИ
·ЛЕКЦИЯ 19 УСИЛИТЕЛИ. ГЕНЕРАТОРЫ
·ЛЕКЦИЯ 20 ИНТЕРФЕРЕНЦИЯ СВЕТА
·ЛЕКЦИЯ 21 ДИФРАКЦИЯ СВЕТА
·ЛЕКЦИЯ 22 ПОЛЯРИЗАЦИЯ СВЕТА
·ЛЕКЦИЯ 23 ГЕОМЕТРИЧЕСКАЯ ОПТИКА
·ЛЕКЦИЯ 24 ГЛАЗ И ЕГО ФУНКЦИИ
·ЛЕКЦИЯ 25 МИКРОСКОПИЯ
·ЛЕКЦИЯ 26 ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
·ЛЕКЦИЯ 27 ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ КВАНТОВОЙ МЕХАНИКИ.
·ЛЕКЦИЯ 28 ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ
·ЛЕКЦИЯ 29 ЛЮМИНЕСЦЕНЦИЯ
·ЛЕКЦИЯ 30 ФОТОБИОЛОГИЧЕСКИЕ ПРОЦЕССЫ
·ЛЕКЦИЯ 31 ЛАЗЕРЫ. ЛАЗЕРНОЕ ИЗЛУЧЕНИЕ
·ЛЕКЦИЯ 32 РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ
·ЛЕКЦИЯ 33 РАДИОАКТИВНОСТЬ
·ЛЕКЦИЯ 34 ДОЗИМЕТРИЯ
·РЕКОМЕНДУЕМАЯ НАУЧНАЯ И НАУЧНО-ПОПУЛЯРНАЯ ЛИТЕРАТУРА
Уравнение Бернулли
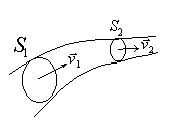
Для идеальной жидкости (сила трения полностью отсутствует) справедливо уравнение, которое было получено швейцарским математиком и физиком Даниилом Бернулли (1700-1782). Рассмотрим тонкую трубку тока и выделим в ней два произвольных сечения (рис. 7.2).
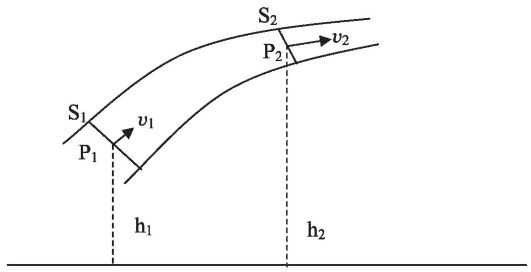 Рис. 7.2.Параметры сечений в трубке тока
Рис. 7.2.Параметры сечений в трубке тока
В общем случае эти сечения находятся на различных высотах (h1 и h2), а их площади различны (S1 и S2). Вследствие уравнения неразрывности различны будут и скорости течения жидкости в этих сечениях (v1и v2). Обозначим давления жидкости в этих сечениях Р1 и Р2 соответственно.
Используя закон сохранения механической энергии, можно доказать, что для этих сечений выполняется следующее соотношение:
 Давление Р называют статическим. Это давление, которое оказывают друг на друга соседние слои жидкости. Его можно измерить манометром, который движется вместе с жидкостью. Величину ρv2/2 называют динамическим давлением. Оно обусловлено движением жидкости. Гидростатическое давление ρgh - это давление, создаваемое весом вертикального столба жидкости высотой h.
Давление Р называют статическим. Это давление, которое оказывают друг на друга соседние слои жидкости. Его можно измерить манометром, который движется вместе с жидкостью. Величину ρv2/2 называют динамическим давлением. Оно обусловлено движением жидкости. Гидростатическое давление ρgh - это давление, создаваемое весом вертикального столба жидкости высотой h.
Уравнение Бернулли формулируется следующим образом:
Измерение скорости жидкости
Установим в разных местах горизонтальной цилиндрической трубы (струи жидкости) одного сечения две трубки: 1) манометрическую трубку, плоскость отверстия которой расположена параллельно движению жидкости; 2) трубку, изогнутую под прямым углом навстречу движению жидкости (трубку Пито) (рис. 7.6).
В движущемся потоке жидкость в трубках поднимается на разную высоту. Давление под манометрической трубкой равно статическому давлению Р. Оно уравновешивается давлением атмосферы Ра и давлением столба жидкости h2:
 Имея систему двух таких трубок, вычисляют скорость потока жидкости по формуле (7.10).
Имея систему двух таких трубок, вычисляют скорость потока жидкости по формуле (7.10).
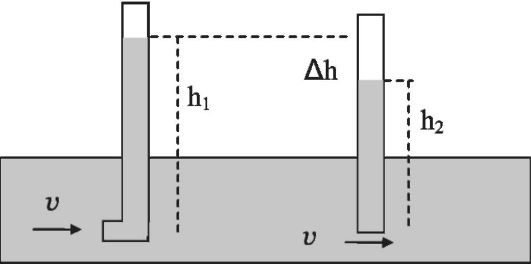 Рис. 7.6.Измерение скорости жидкости
Рис. 7.6.Измерение скорости жидкости
Инжектор
Этот прибор используют для дозированной подачи пациенту газообразного препарата. Например, закиси азота или кислорода. Препарат из баллона поступает в смесительную камеру через узкое сопло (рис. 7.7).
При этом скорость движения препарата возрастает, а его давление, в соответствии с уравнением Бернулли, падает. В смесительной камере возникает разрежение, и в нее засасывается атмосферный воздух. Всасывание происходит через одно из отверстий поворотного диска. Отверстия имеют различные диаметры. Выбирая соответствующее отверстие, регулируют состав смеси, подаваемой пациенту.
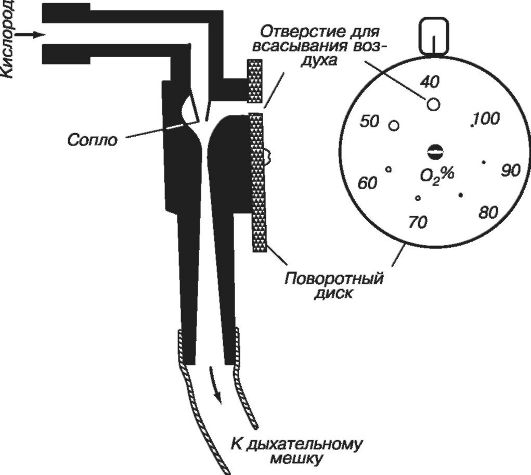 Рис. 7.7.Подача кислорода при кислородной терапии
Рис. 7.7.Подача кислорода при кислородной терапии
Ингалятор
Этот прибор используют для введения в область носоглотки лекарственных средств в распыленном виде (рис. 7.8).
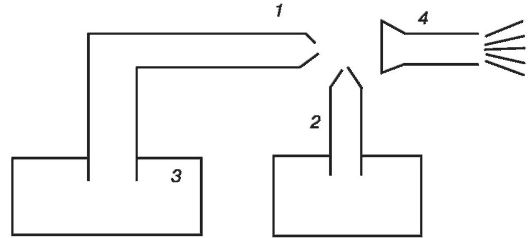 Рис. 7.8.Схема ингалятора
Рис. 7.8.Схема ингалятора
Он состоит из двух трубок, расположенных под прямым углом.
Горизонтально расположенная трубка (1) имеет на конце сужение. Чуть ниже этого конца располагается верхний конец вертикальной трубки (2), нижний конец которой опущен в сосуд с жидким препаратом. В горизонтальную трубку подается пар (3). При прохождении суженного конца скорость пара возрастает, а давление падает. В область пониженного давления засасывается препарат, который распыляется струей пара. В результате образуется смесь пара, воздуха и капелек препарата, которая через патрубок (4) поступает к пациенту.
Основные понятия и формулы
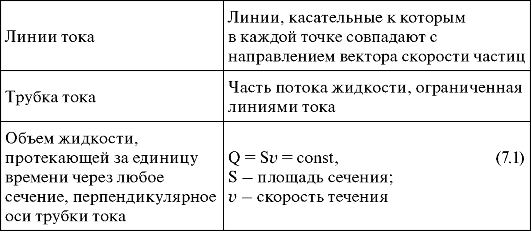 Продолжение таблицы
Продолжение таблицы
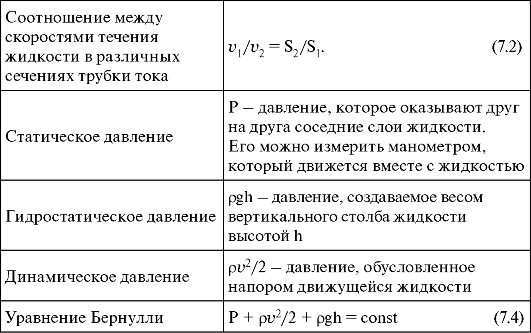 7.6. Задачи
7.6. Задачи
 2.Кровь течет по горизонтальному участку артерии, имеющему сужение. Где давление крови на стенки сосуда будет больше - на суженном или широком участке? Динамическим или статическим давлением обусловлено фонтанирование крови при надрезе артерии?
2.Кровь течет по горизонтальному участку артерии, имеющему сужение. Где давление крови на стенки сосуда будет больше - на суженном или широком участке? Динамическим или статическим давлением обусловлено фонтанирование крови при надрезе артерии?
Решение
Фонтанирование крови при надрезе артерии обусловлено разностью между статическим давлением в артерии и давлением атмосферы.
При прохождении места сужения скорость кровотока возрастает (7.2), а статическое давление, которое и воздействует на стенки сосуда, уменьшается (7.5). Отметим, что вклад динамического давления в полное давление ничтожен. Действительно, принимая v = 0,5 м/с, ρ = 103 кг/м3, найдем:
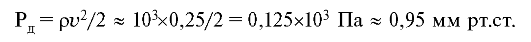 Ответ: давление на стенки незначительно уменьшается на участке сужения артерии. Фонтанирование крови при надрезе артерии обусловлено статическим давлением.
Ответ: давление на стенки незначительно уменьшается на участке сужения артерии. Фонтанирование крови при надрезе артерии обусловлено статическим давлением.
3.Скорость потока крови в капиллярах равна примерно v1= 30 мм/мин, а скорость потока крови в аорте v2= 45 см/с. Определить, во сколько раз площадь сечения всех капилляров больше сечения аорты.
 4.Лекарственный раствор вводят в мышцу животного с помощью шприца, внутренний диаметр которого d1 = 10 мм, а диаметр иглы d2 = 0,5 мм. Определить скорость истечения раствора из иглы, если скорость перемещения поршня шприца равна v1 = 2,3 см/с.
4.Лекарственный раствор вводят в мышцу животного с помощью шприца, внутренний диаметр которого d1 = 10 мм, а диаметр иглы d2 = 0,5 мм. Определить скорость истечения раствора из иглы, если скорость перемещения поршня шприца равна v1 = 2,3 см/с.
 7. Наблюдая под микроскопом эритроциты в капилляре, можно измерить скорость течения крови: v1= 0,5 мм/с. Средняя скорость тока крови в аорте составляет v2= 40 см/с. На основании этих данных определить, во сколько раз суммарная площадь поперечных сечений функционирующих капилляров больше площади сечения аорты.
7. Наблюдая под микроскопом эритроциты в капилляре, можно измерить скорость течения крови: v1= 0,5 мм/с. Средняя скорость тока крови в аорте составляет v2= 40 см/с. На основании этих данных определить, во сколько раз суммарная площадь поперечных сечений функционирующих капилляров больше площади сечения аорты.
Решение
Условие неразрывности струи было получено для трубки тока переменного сечения. Очевидно, что оно применимо и к разветвлению труб. В задаче такое разветвление начинается с аорты (площадь поперечного сечения S2) и заканчивается капиллярами (общая площадь сечения S1). Исходя из этого запишем уравнение неразрывности струи (7.2): S1/S2 = v2/v1= 800.
Ответ: 800.
8.При всасывании человек может понизить давление в легких на 80 мм рт.ст. ниже атмосферного. Определить, на какую высоту ему удастся втянуть воду по трубочке.
 10.Во время бури или смерча с домов иногда срывает крыши. Используя уравнение Бернулли, объяснить, почему это происходит. Решение
10.Во время бури или смерча с домов иногда срывает крыши. Используя уравнение Бернулли, объяснить, почему это происходит. Решение
Давление в потоке ветра уменьшается. Поэтому давление на чердаке превышает внешнее давление на величину ΔΡ = pv2/2. При этом на кровлю действует направленная наружу сила F = Spv2/2. При скорости v = 35 м/с (ураган), ρ = 1,3 кг/м3 и S = 100 м2 величина силы составляет F = 61 000 Н (6 т), что существенно превышает вес кровли.
Линия тока. Трубка тока
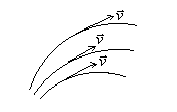
При рассмотрении динамики движения жидкости или газа можно не следить за конкретной точкой среды, а следить за конкретной точкой пространства и фиксировать в таких точках направление и величину скорости различных частиц в данный момент времени. Таким образом, в каждой точке пространства можно получить некоторый вектор, имеющий определённую величину и направление. Такая картина называется полем скоростей. В этом поле скоростей можно провести некоторые линии, линии тока (так же, как проводят силовые линии в электрическом или гравитационном полях) (см. рис .1).
Линия тока (на рис. 1 выделены жёлтым) – линия в пространстве, направление касательной к которой в данный момент времени в каждой точке совпадает с направлением вектора скорости в этой точке.

Рис. 1. Линии тока в поле скоростей
Если сделать мгновенное отображение, то можно поле скоростей заменить линиями тока.
В том случае, когда скорости в данной точке пространства не меняются со временем, такое движение называют стационарным движением жидкости или газа. В этом случае картина линий тока не будет зависеть от времени, она будет заморожена. Линия тока в данном случаи будет представлять собой траекторию движения отдельной частицы, которая будет двигаться в каждый момент времени в направлении касательных к этой линии.
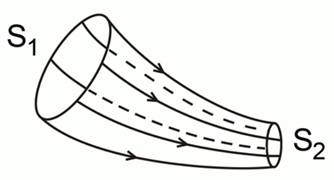
Рис. 2. Трубка тока
При стационарном течении жидкости или газа из стационарных линий тока можно построить поверхность такой формы, которая называется трубкой тока (см. рис. 2). Эта трубка – мысленно выделенная труба, по которой течёт жидкость или газ (далее будет рассматриваться движение жидкости именно в такой трубе). Если за определённое время некоторая масса жидкости перетекла через поверхность сечения такой трубы  , то такое же количество жидкости должно перетечь через сечение трубы
, то такое же количество жидкости должно перетечь через сечение трубы  , так как с течением времени полная масса жидкости в этом объёме, выделенным двумя сечениями, меняться не должна.
, так как с течением времени полная масса жидкости в этом объёме, выделенным двумя сечениями, меняться не должна.
Уравнение Бернулли
Динамика движения реальной жидкости очень сложная, однако в некоторых случаях можно пренебречь вязкостью жидкости, то есть наличием трения между различными слоями жидкости. В этом случае при движении жидкости не выделяется тепло, то есть сохраняется механическая энергия. Закон движения такой идеальной несжимаемой жидкости без вязкости называется уравнением Бернулли, которое полностью основано на законе сохранения механической энергии.
Рассмотрим энергетические соотношения при движении идеальной несжимаемой жидкости. Выделяем некоторую трубку тока, ограниченную сечениями  и
и  (см. рис. 3). За некоторое время
(см. рис. 3). За некоторое время 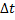 масса жидкости, заключённой между сечениями
масса жидкости, заключённой между сечениями 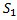 и
и  , сместится. Сечение
, сместится. Сечение  перейдёт в сечение
перейдёт в сечение 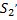 , а
, а 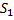 – в
– в 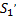 .
.
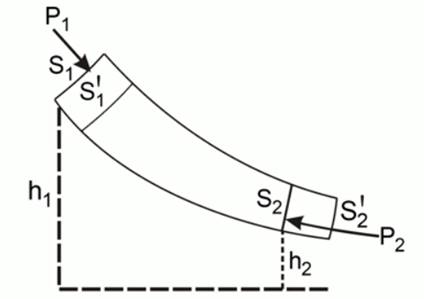
Рис. 3. Трубка тока
Рассматриваем не только очень маленькие сечения трубки тока, но и очень маленькие промежутки времени, в течение которых сечения сместятся на очень маленькую величину. Будем пренебрегать изменением площади сечений, изменением высоты, скорости и давления на этих сечениях. С учётом этих данных рассчитаем работу внешних сил над данным объёмом жидкости. Эта работа складывается из таких работ:
1) Внешняя часть жидкости давит на сечение  с силой
с силой  , поэтому совершает работу при перемещении этого сечения.
, поэтому совершает работу при перемещении этого сечения.
2) Внешняя часть жидкости давит на сечение  с силой
с силой 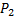 и совершает отрицательную работу при перемещении этого сечения.
и совершает отрицательную работу при перемещении этого сечения.
Также меняется кинетическая и потенциальная энергия жидкости.
Для того чтобы легче было это понять, рассмотрим объём жидкости, заключённый между сечениями 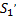 и
и  . Энергия, масса, скорость, давление и остальные характеристики этого объёма не изменились в силу стационарности движения. Поэтому вся работа внешних сил привела к тому, что энергия части жидкости между
. Энергия, масса, скорость, давление и остальные характеристики этого объёма не изменились в силу стационарности движения. Поэтому вся работа внешних сил привела к тому, что энергия части жидкости между 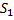 и
и 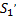 переместилась в часть между
переместилась в часть между 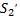 и
и  с ниже посчитанными изменениями:
с ниже посчитанными изменениями:
-работа внешних сил в верхней части трубки: 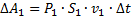 ;
;
-работа внешних сил в нижней части трубки ( 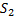 сдвигается в сторону противоположную силе давления, поэтому работа имеет знак минус):
сдвигается в сторону противоположную силе давления, поэтому работа имеет знак минус): 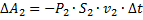 ;
;
-суммарная работа, произведённая над объёмом, передвинувшимся за время 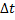 :
: 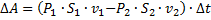 .
.
Вычислим изменение энергии рассмотренного отрезка трубки тока (изменение энергии части жидкости между 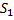 и
и 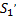 по сравнению с энергией между
по сравнению с энергией между 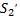 и
и  ), для этого из энергии конечной отнимаем энергию начальную.
), для этого из энергии конечной отнимаем энергию начальную.
Изменение потенциальной энергии (потенциальная энергия – это масса (масса – это плотность ( 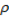 ), умноженная на объём, а объём в данном случае – это поперечное сечение на длину участка между
), умноженная на объём, а объём в данном случае – это поперечное сечение на длину участка между 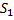 и
и 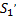 или
или 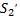 и
и  (
( 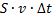 )), умноженная на ускорение свободного падения (
)), умноженная на ускорение свободного падения ( 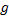 ) и высоту этого участка над некоторым нулевым уровнем):
) и высоту этого участка над некоторым нулевым уровнем):
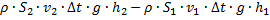 .
.
Изменение кинетической энергии (масса, умноженная на квадрат скорости и делённая на два): 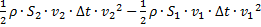 .
.
Изменение энергии в соответствии с законом сохранения энергии равно работе внешних сил.
Приравниваем эти величины и переносим слагаемые с одинаковыми индексами в одну сторону. Сократив 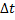 ,
, 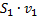 и
и 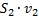 (согласно условию неразрывности
(согласно условию неразрывности 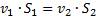 ), получаем окончательный результат:
), получаем окончательный результат: 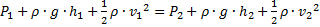 .
.
Сечения 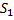 и
и  были выбраны произвольно, поэтому уравнение можно записать в таком виде:
были выбраны произвольно, поэтому уравнение можно записать в таком виде: 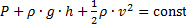 .
.
Мы получили уравнение Бернулли. Это уравнение утверждает, что сумма физических величин ( 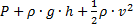 ) постоянна вдоль очень узкой трубки тока. В математическом смысле следует устремить сечение этой трубки к нулю, то есть получим линию тока. Следовательно,
) постоянна вдоль очень узкой трубки тока. В математическом смысле следует устремить сечение этой трубки к нулю, то есть получим линию тока. Следовательно, 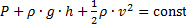 вдоль любой линии тока.
вдоль любой линии тока.
Уравнение Бернулли.
Изучение движения реальных жидкостей и газов, вообще говоря, представляет собой довольно сложную задачу. Для ее упрощения сначала полностью пренебрегают силами внутреннего трения, считая жидкости идеальными.
Рассмотрим стационарное течение идеальной жидкости в каком-либо консервативном силовом поле, например в поле силы тяжести.[1] Применим к этому течению закон сохранения энергии. При этом будем полностью пренебрегать теплообменом, который может происходить между частями жидкости с окружающей средой. Выделим в жидкости бесконечно узкую трубку тока и рассмотрим часть жидкости, занимающую объем MNDC.
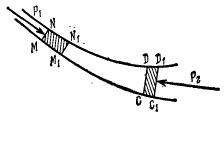
Пусть эта часть переместилась в бесконечно близкое положение M1N1D1C1. Вычислим работу А, совершаемую при этом силами давления. Давление, действующее на боковую поверхность трубки тока, перпендикулярно к перемещению и работы не совершает. При перемещении границы MN в положение M1N1 совершается работа A1 = p1S1l1, где l1 = MM1 – величина перемещения. Введя объем ∆1V = S1l1, ее можно представить в виде A1 = p1∆1V или 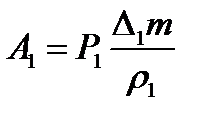 , где
, где 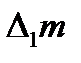 — масса жидкости в объеме MNN1M1. При перемещении границы CD в положение C1D1 жидкость совершает работу против давления Р2 (или давление Р2 совершает над жидкостью отрицательную работу). Для нее, рассуждая аналогично, найдем
— масса жидкости в объеме MNN1M1. При перемещении границы CD в положение C1D1 жидкость совершает работу против давления Р2 (или давление Р2 совершает над жидкостью отрицательную работу). Для нее, рассуждая аналогично, найдем 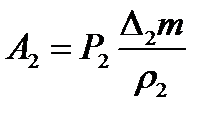 , где
, где 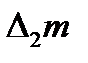 — масса жидкости в объеме
— масса жидкости в объеме 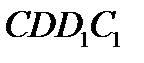 . Но если движение стационарно, то масса жидкости в объеме M1N1DC не изменится, а потому из закона сохранения массы получим
. Но если движение стационарно, то масса жидкости в объеме M1N1DC не изменится, а потому из закона сохранения массы получим 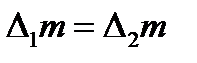 . Опуская индексы у
. Опуская индексы у 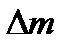 , для работы, совершаемой внешним давлением, окончательно находим
, для работы, совершаемой внешним давлением, окончательно находим
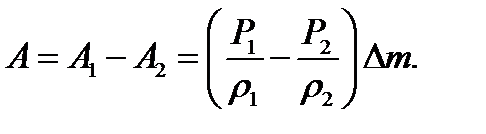
Эта работа должна быть равна приращению 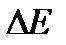 полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме M1N1DC не изменилась. Поэтому величина
полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме M1N1DC не изменилась. Поэтому величина 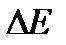 равна разности энергий массы жидкости
равна разности энергий массы жидкости 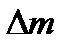 в положениях CDD1С1 и MNN1M1. Обозначая посредством ε полную энергию, приходящуюся на единицу массы жидкости, находим
в положениях CDD1С1 и MNN1M1. Обозначая посредством ε полную энергию, приходящуюся на единицу массы жидкости, находим 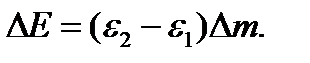 Приравнивая эту величину работе А и сокращая на
Приравнивая эту величину работе А и сокращая на 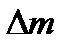 , получаем
, получаем
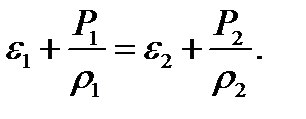
Отсюда следует, что вдоль одной и той же линии тока при стационарном течении идеальной жидкости величина 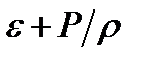 остается постоянной:
остается постоянной:
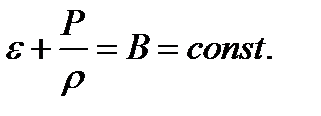
Это соотношение называется уравнением Даниила Бернулли (1700—1782), который впервые опубликовал его в 1738 году. При выводе уравнения Бернулли мы нигде не использовали предположения о несжимаемости жидкости. Поэтому оно справедливо и для сжимаемых жидкостей. Требуется только, чтобы жидкость была идеальной, а течение – стационарным.
Если жидкость несжимаемая, то вся энергия ε складывается из кинетической энергии единицы массы жидкости 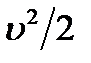 и ее потенциальной энергии gh в поле тяжести. В этом случае уравнение Бернулли принимает вид
и ее потенциальной энергии gh в поле тяжести. В этом случае уравнение Бернулли принимает вид
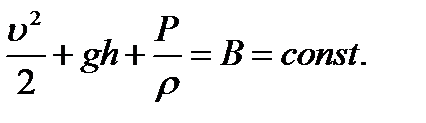
Подчеркнем, что это постоянство этой величины выполняется только вдоль одной и той же линии тока. Вообще говоря, она может меняться при переходе от одной линии тока к другой. Но могут быть и такие случаи, где постоянная Бернулли одна и та же для всего потока жидкости. Рассмотрим один довольно часто встречающийся частный случай. Допустим, что все линии тока начинаются или оканчиваются в такой области, где жидкость практически находится в состоянии покоя. Возьмем одну из точек линии тока в этой области. Тогда в уравнении Бернулли следует считать v = 0 и мы получим
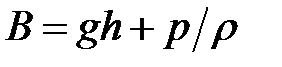 .
.
Но во всей области, где жидкость покоится, должно выполняться условие 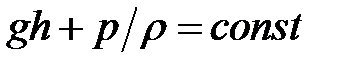 , так как давление в покоящейся жидкости одинаково (при соответствующем введении начала координат направления оси это представляет собой условие равновесия). Поэтому в рассматриваемом случае постоянная Бернулли для всех линий тока будет одинаковой.
, так как давление в покоящейся жидкости одинаково (при соответствующем введении начала координат направления оси это представляет собой условие равновесия). Поэтому в рассматриваемом случае постоянная Бернулли для всех линий тока будет одинаковой.
Допустим теперь, что тонкая трубка тока имеет переменное поперечное сечение, а ось ее горизонтальна. (Примером может служить горизонтальная труба переменного сечения, по которой течет жидкость). Тогда h — const, и уравнение Бернулли принимает вид
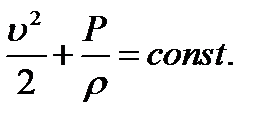
 Отсюда видно, что давление больше там, где меньше скорость v, и наоборот. С другой стороны, согласно соотношению
Отсюда видно, что давление больше там, где меньше скорость v, и наоборот. С другой стороны, согласно соотношению 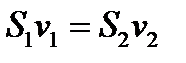 , скорость v минимальна там, где максимально сечение трубки. Значит, в широких частях трубки давление максимально, а в узких — минимально. Такой результат является непосредственным следствием второго закона Ньютона. Действительно, когда жидкость из широкой части течет в узкую, то скорость ее возрастает. Значит, ускорение направлено в сторону течения, т.е. на рис. слева направо. Это ускорение сообщается разностью давлений, действующих на рассматриваемую часть жидкости слева и справа. Следовательно, давление слева, т. е. в более широкой части трубки, должно быть больше, чем справа, где трубка уже.
, скорость v минимальна там, где максимально сечение трубки. Значит, в широких частях трубки давление максимально, а в узких — минимально. Такой результат является непосредственным следствием второго закона Ньютона. Действительно, когда жидкость из широкой части течет в узкую, то скорость ее возрастает. Значит, ускорение направлено в сторону течения, т.е. на рис. слева направо. Это ускорение сообщается разностью давлений, действующих на рассматриваемую часть жидкости слева и справа. Следовательно, давление слева, т. е. в более широкой части трубки, должно быть больше, чем справа, где трубка уже.
Рассмотрим несколько примеров, иллюстрирующих следствия из уравнения Бернулли.
Пульверизатор.
Возьмем трубку с суживающимся наконечником и будем продувать через нее воздух. Давление воздуха в узкой части наконечника и в выходящей из него струе будет меньше атмосферного.
Поднесем теперь струю воздуха к верхнему концу стеклянной трубки, нижний конец которой погружен в воду, а верхний оканчивается узким наконечником (рис. 2.3, а). Вода в стеклянной трубке будет подниматься, разбрызгиваться и увлекаться струей воздуха. На этом принципе основано устройство пульверизатора.
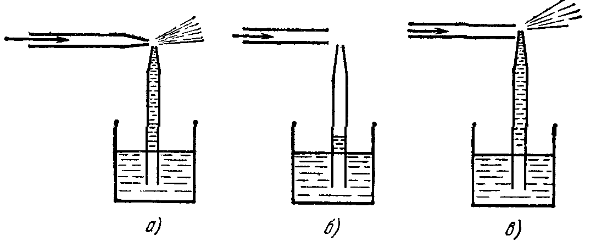
Рис. 2.3.
Если трубка, по которой продувается воздух, не снабжена узким наконечником, а имеет постоянное поперечное сечение (рис. 2.3, б), то поднятие воды и разбрызгивание не происходит. Если, однако, такую трубку поднести вплотную к наконечнику трубки, погруженной в воду, так, чтобы между ними образовался узкий зазор (рис.2.3,в), то вода опять поднимается и разбрызгивается. Зазор между трубками выполняет роль узкого наконечника, понижающего давление воздуха в струе.
Рассмотрим другой пример.
Если два слегка изогнутых листа твердой бумаги подвесить на горизонтальных проволоках (рис. 2.4) и продувать между ними воздух, то они притягиваются друг к другу. Дело в том, что давление воздуха Р между листами в наиболее узком месте
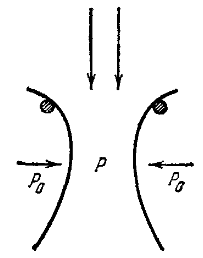
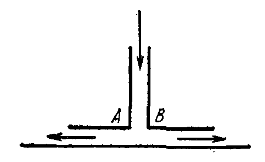
Рис. 2.5.
становится меньше атмосферного Р0, и наружное атмосферное давление прижимает листы друг к другу. Можно также подвесить на небольшом расстоянии друг от друга две стеклянные колбы. При продувании воздуха между ними колбы начинают стучать, сталкиваясь друг с другом. Притяжение такого же типа наблюдается между двумя кораблями, когда они идут параллельным курсом на небольшом расстоянии друг от друга. Это легко объяснить, если перейти в систему отсчета, в которой корабли покоятся, а вода течет между ними. Описанное явление не раз было причиной столкновения судов и приводило к авариям.
3. Формула Торричелли. Кавитация. Форма струи жидкости
Уравнение Бернулли имеет самое широкое применение на практике. В качестве первого примера рассмотрим стационарное истечение идеальной несжимаемой жидкости из сосуда (рис.2.6). Если полагать, что сосуд достаточно велик, а отверстие мало, то можно считать, что при истечении уровень жидкости не изменяется заметно в течение достаточно продолжительного промежутка времени. Пусть на поверхность жидкости в сосуде действует давление 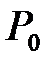 (например, атмосферное). Будем также полагать, что струя вытекает в пространство, где внешнее давление также равно
(например, атмосферное). Будем также полагать, что струя вытекает в пространство, где внешнее давление также равно 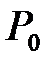 (истечение в атмосферу). Обобщение на различные давления не составляет труда. Проведем некоторую гипотетическую линию тока и выберем на ней две точки: одну на поверхности жидкости в сосуде (точка 1), другую внутри отверстия (точка 2).
(истечение в атмосферу). Обобщение на различные давления не составляет труда. Проведем некоторую гипотетическую линию тока и выберем на ней две точки: одну на поверхности жидкости в сосуде (точка 1), другую внутри отверстия (точка 2).
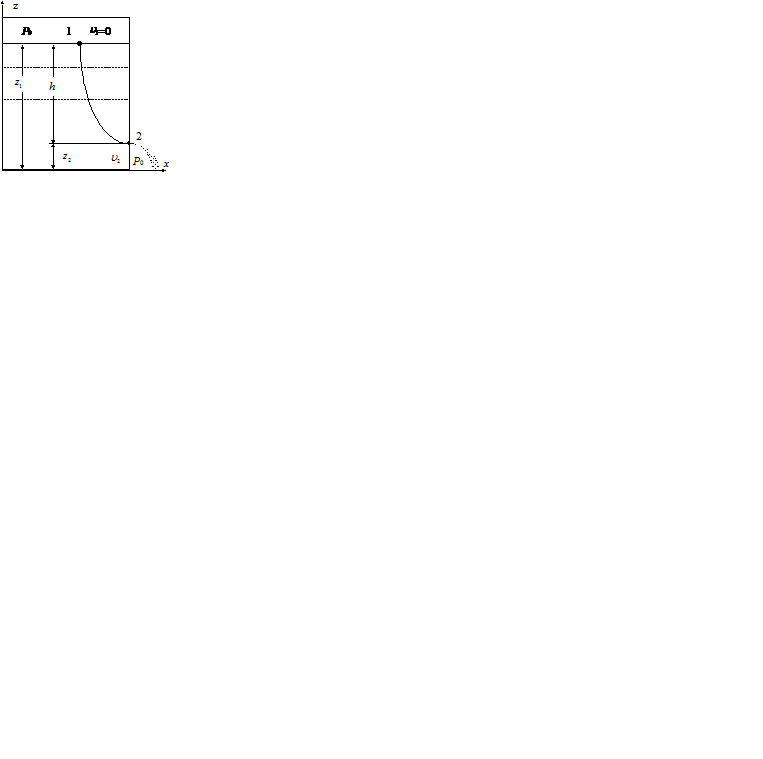 Рис.2.6. Рис.2.6. | Тогда для этой линии тока можно записать уравнение Бернулли: 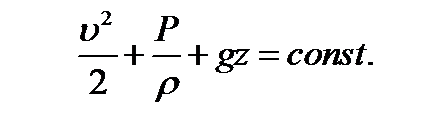 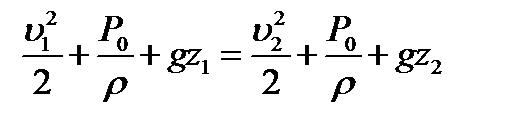 Поскольку поверхность жидкости в сосуде предполагается неподвижной Поскольку поверхность жидкости в сосуде предполагается неподвижной 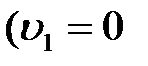 ), из последнего равенства следует: Это соотношение называется формулой Торричелли. Заметим, что такую же скорость приобретает тело, которое падает в пустоте с высоты h. С помощью формулы Торричелли, можно оценить, за какое время жидкость полностью истечет из сосуда. ), из последнего равенства следует: Это соотношение называется формулой Торричелли. Заметим, что такую же скорость приобретает тело, которое падает в пустоте с высоты h. С помощью формулы Торричелли, можно оценить, за какое время жидкость полностью истечет из сосуда. |
Задача о вытекании жидкости из сосуда.
Пусть внизу сосуда имеется отверстие площадью S0, а в самом сосуде начальная высота уровня жидкости равна h0. Нужно найти зависимость высоты уровня жидкости от времени. За какое время жидкость полностью вытечет из сосуда?
Применим формулу Торричелли для скорости жидкости:
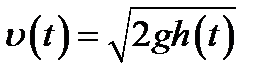 .
.
Тогда объем жидкости, вытекающий в секунду из сосуда, может быть рассчитан, как
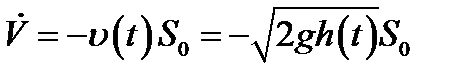 .
.
Но с другой стороны, объем равен:
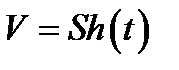 .
.
Таким образом, получаем дифференциальное уравнение:
.
Разделяем переменные и интегрируем:


 pallet-okna.ru
pallet-okna.ru  Остекление и отделка балконов за 2 дня! Скидка 50%! Звоните!Адрес и телефонВоронежСкрыть объявлениеСкрытьрекламу:Не интересуюсь этой темой / Уже купилНавязчивое и надоелоСомнительного содержания или спамМешает просмотру контента
Остекление и отделка балконов за 2 дня! Скидка 50%! Звоните!Адрес и телефонВоронежСкрыть объявлениеСкрытьрекламу:Не интересуюсь этой темой / Уже купилНавязчивое и надоелоСомнительного содержания или спамМешает просмотру контента  balconych.ru
balconych.ru  Качественное остекление балконов «под ключ» от профи. Бесплатный замерХолодноеостеклениеТеплоеостеклениеОтделка и утеплениеРассрочкаСкрыть объявлениеСкрытьрекламу:Не интересуюсь этой темой / Уже купилНавязчивое и надоелоСомнительного содержания или спамМешает просмотру контента
Качественное остекление балконов «под ключ» от профи. Бесплатный замерХолодноеостеклениеТеплоеостеклениеОтделка и утеплениеРассрочкаСкрыть объявлениеСкрытьрекламу:Не интересуюсь этой темой / Уже купилНавязчивое и надоелоСомнительного содержания или спамМешает просмотру контента  окналидер.рф
окналидер.рф  Быстрое изготовление! Монтаж по ГОСТ! Гарантия 5 лет!ЦеныВсе услугиСертификатыКонтактыАдрес и телефонВоронежСкрыть объявлениеСкрытьрекламу:Не интересуюсь этой темой / Уже купилНавязчивое и надоелоСомнительного содержания или спамМешает просмотру контента
Быстрое изготовление! Монтаж по ГОСТ! Гарантия 5 лет!ЦеныВсе услугиСертификатыКонтактыАдрес и телефонВоронежСкрыть объявлениеСкрытьрекламу:Не интересуюсь этой темой / Уже купилНавязчивое и надоелоСомнительного содержания или спамМешает просмотру контента