Энергия покоя является внутренней энергией тела.

Внутренняя энергия тела складывается из кинетической энергии всех частиц относительно центра масс, потенциальной энергии их взаимодействия и суммы энергий покоя всех частиц.

Закон сохранения релятивистской массы и энергии:изменение полной энергии тела (или системы) DЕ сопровождается эквивалентным изменением её массы (Dm): Dm=DE/c², DE=Dmc².

Смысл энергосодержания тела:существует принципиальная возможность перехода материальных объектов, имеющих массу покоя, в электромагнитном излучении, не имеющее массы покоя, при этом выполняется закон сохранения энергии.

Основной закон релятивистской дянамвкя материальной точки имеет вид

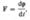
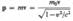
В силу однородности пространства в релятивистской механике выполняет­ся закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени

Релятивистский закон сложения скоростей. Рассмотрим движение материальной точки в системе К', в свою очередь движущейся относительно системы К со скоро­стью v . Определим скорость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется координатами х, у, х, а в системе

системе К, то, определяя его длину в системе К', опять-таки придем к выражению. Линейные размеры размеры тела, движущегося относительно инерциальной системы отсчета,уменьшается в направлении движения в корень из 1-β2 -лоренцево сокращение длинны,тем больше, чем больше скорость движения.

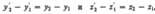
т. е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.

18. Статистический и термодинамический методы исследования.

В физике для описания тепловых явлений используют два основных метода: молекулярно-кинетический (статистический) и термодинамический. Молекулярно-кинетический метод основан на представлении о том, что все вещества состоят из молекул, находящихся в хаотическом движении. Так как число молекул огромно, то можно, применяя законы статистики, найти определённые закономерности для всего вещества в целом. Термодинамический метод исходит из основных опытных законов, получивших название законов термодинамики. Термодинамический метод подходит к изучению явлений подобно классической механике, которая базируется на опытных законах Ньютона. При таком подходе не рассматривается внутреннее строение вещества.

https://studfiles.net/preview/5616181/page:6/

19. Идеальный газ.

Идеальным называют такой газ, для которого можно пренебречь размерами молекул, силами молекулярного взаимодействия; соударения молекул в таком газе происходят по закону соударения упругих шаров.

Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объём V, давление p и температура T.

Среднеквадратичная скорость молекул.

<u>=Ö(3RT/M).

Молекулярно-кинетическое толкование абсолютной температуры.

Для однозначного определения температуры необходим выбор термодинамического тела и термодинамического параметра.

Температурный параметр должен изменяться с температурой непрерывно и монотонно, т.е. он не должен иметь одинаковые значения при разной температуре.

В настоящее время применяют только две температурные шкалы: термодинамическую, градуированную в кельвинах, и Международную практическую, градуированную в градусах Цельсия.

Термодинамическая температура и температура по Международной практической шкале связаны соотношением T=273.15°C+t.

25. Первое начало термодинамики.

Первое начало термодинамики формулируется в виде следующего утверждения: невозможно построить перпетууммобиле первого рода.

Первое начало термодинамики – это закон сохранения и превращения энергии: при разнообразных процессах, протекающих в природе, энергия не возникает из ничего и не уничтожается, но превращается лишь из одних видов в другие.

Изменение внутренней энергии тела равно разности сообщённого телу количества теплоты и произведённой над ним механической работы: dU=dQ-dA.

21. Закон Максвелла для распределения молекул идеального газа по скоростям теплового движения.

Скорости молекул газа имеют различные значения и направления, причём как величина, так и направление скорости каждой отдельной молекулы изменяется в результате соударений, поэтому нельзя определить число молекул, обладающих точно заданной скоростью в данный момент времени, но можно подсчитать число молекул, скорости которых лежат в интервале от u1 до u2.

При этом предполагалось, что в газе не существует молекул, имеющих в точности одинаковые скорости, и число молекул dN, скорость которых лежит в узком интервале междуu и u+du, пропорционально общему числу молекул N, ширине интервала du и зависит от скорости u. Такая теоретическая зависимость была установлена Максвеллом на основании теории вероятностей:

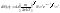
Функцию

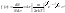
22.Вероятностное толкование закона распределения Максвелла. Барометрическая формула.

p=p₀e^(-mgh/(kT)) – барометрическая формула.

Эта формула показывает зависимость давления газа от высоты над поверхностью Земли. Если учесть, что концентрация молекул воздуха в атмосфере определяет давление, то эту формулу можно записать в виде n=n₀e^(-mgh/(kT)).

Из этой формулы следует, что с понижением температуры число частиц на высоте, отличной от нуля, убывает и при T=0 K обращается в нуль, т.е. при 0 К все молекулы расположились бы на земной поверхности.

https://studfiles.net/preview/5616181/page:7/

Закон Больцмана для распределения частиц идеального газа во внешнем потенциальном поле.

Так как потенциальная энергия молекул на различной высоте различна и на высоте h определяется по формуле Еп=mgh, то n=n₀e^(-Eп/(kT)) – закон Больцмана, показывающий распределение участвующих в тепловом движении молекул в потенциальном поле сил, в частности в поле силы тяжести.

Закон Больцмана является универсальным, он справедлив для любых частиц, находящихся в потенциальном поле сил.

23. Среднее число столкновений и средняя длина свободного пробега молекул идеального газа.

Проследить точно за траекторией частицы, пришедшей из точки А в точку В, невозможно, поэтому реальное смещение молекуле в газе оценивают скоростью диффузии: (отношением перемещения L молекулы из А в В к времени, за которое произошло это перемещение). Скорость диффузии молекулы значительно меньше средней скорости её молекулярного движения.

Чтобы оценить скорости диффузии молекул, вводится понятие средней длины свободного пробега<l>. Это такой путь, который молекула проходит, не испытывая соударений.

Средняя длина свободного пробега молекулы равна отношению пути, пройденного молекулой за 1 с, к числу происшедших за это время столкновений:<l>=<u>/<z>=1/(4Ö2pr²n₀).

24.Внутренняя энергия идеального газа.

Внутренняя энергия – это сумма энергий молекулярных взаимодействий и энергии теплового движения молекул.

Внутренняя энергия системы зависит только от её состояния и является однозначной функцией состояния.

Внутренняя энергия идеального газа пропорциональна массе газа и его термодинамической температуре.

Работа газа при расширении.

Пусть в цилиндре под поршнем находится газ, занимающий объём V под давлением p. Площадь поршня S. Сила, с которой газ давит на поршень, F=pS. При расширении газа поршень понимается на высоту dh, при этом газ совершает работу dA=Fdh=pSdh. Но Sdh=dV – увеличение объёма газа. Следовательно элементарная работа dA=pdV. Полную работу A, совершаемую газом при изменении его объёма от V1 до V2 найдём интегрированием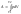

Результат интегрирования зависит от процесса, протекающего в газах.

При изохорном процессе V=const, следовательно, dV=0 и A=0.

При изобарном процессе p=const, тогда

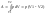
Работа при изобарном расширении газа равна произведению давления газа на увеличение объёма.

При изотермическом процессе T=const. p=(mRT)/(MV).

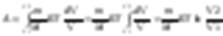
Количество теплоты.

Энергия, переданная газу путём теплообмена, называется количеством теплоты Q.

При сообщении системе бесконечно малого количества теплоты dQ его температура изменится на dT.

26.Теплоёмкостью С системы называют величину, равную отношению сообщенного системе количества теплоты dQ к изменению температуры dT системы: C=dQ/dT.

Различают удельную теплоёмкость (теплоёмкость 1 кг вещества) c=dQ/(mdT) и молярную теплоёмкость (теплоёмкость 1 моль вещества) c=Mc.

При различных процессах, протекающих в термодинамических системах, теплоёмкости будут различны.

https://studfiles.net/preview/5616181/page:8/

27. Адиабатный процесс.

Процесс, протекающий без теплообмена с окружающей средой, называют адиабатным.

Первое начало термодинамики для адиабатного процесса имеет вид: dU+dA=0.

При адиабатном процессе работа совершается только за счёт изменения внутренней энергии газа, т.е. pdV= -C_VdT, откуда dT=-pdV/C_V.

pV^g=const

TV^-1=const

T^p1-^ – уравнениеПуассона. Оно связывает параметры состояния газа при адиабатном процессе.

g=C_P/C_V=(i+2)/i.

если процесс может быть проведён в обратном направлении, причём система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности, то эти процессы называют обратимыми.

28. Тепловые двигатели и холодильные машины.

Тепловой двигатель представляет собой устройство, превращающее внутреннюю энергию топлива в механическую. Энергия, выделяющаяся при сгорании топлива, путём теплообмена передаётся газу. Газ, расширяясь, совершает работу против внешних сил, приводя в движение механизм.

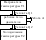Любой тепловой двигатель состоит из трёх основных частей: рабочего тела, нагревателя и холодильника. По окончании цикла рабочее тело возвращается в свое первоначальное состояние, его внутренняя энергия

принимает начальное значение.

Реальные тепловые двигатели работают по разомкнутому циклу, т.е. после расширения газ выбрасывается, а в машину вводится и сжимается новая порция газа.

Величина h=A/Q=(Q1-Q2)/Q1 называется термическим коэффициентом полезного действиядля кругового процесса.

29.Цикл Карно для идеального газа и его кпд.

Цикл Карно это обратимый круговой процесс, состоящий из двух равновесных изотермических и двух равновесных адиабатных процессов, чередующихся между собой.

h=(T1-T2)/T1.

30. Второе начало термодинамики.

Второе начало термодинамики определяет направление процессов, происходящих в природе и связанных с превращением энергии.

Превращение теплоты в работу возможно только при наличии нагревателя и холодильника; во всех тепловых машинах полезно используется только часть энергии, передаваемая от нагревателя к холодильнику.

Иначе говоря, ни один тепловой двигатель не может дать КПД, равный единице.

В природе невозможен процесс, единственным результатом которого был бы переход теплоты полностью в работу.

Статистическое толкование второго начала термодинамики.

Связь энтропии с термодинамической вероятностью установил Больцман – энтропия пропорциональна логарифму термодинамической вероятности: S=klnW.

Статистический смысл понятия энтропии состоит в том, что увеличение энтропии изолированной системы связано с переходом этой системы из менее вероятного состояния в более вероятное.

Одной из формулировок второго закона термодинамики, выявляющей статистический характер этого закона, является формулировка Больцмана: все процессы в природе протекают в направлении, приводящем к увеличению вероятности состояния.

https://studfiles.net/preview/5616181/page:9/

Энтропия в термодинамике.

Величина, равная отношению теплоты, полученной телом при изотермическом процессе, к температуре, при которой происходит теплопередача, т.е. Q/T, называется приведённой теплотой.

Алгебраическая сумма приведённыхтеплот для обратимого цикла Карно равна нулю.

Функция, характеризующая направление протекания самопроизвольных процессов в замкнутой термодинамической системе, называется энтропией: .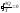

Каждому состоянию тела соответствует одно определённое значение энтропии. Поэтому энтропия является однозначной функцией состояния.

31. Энтропия в термодинамике.

Величина, равная отношению теплоты, полученной телом при изотермическом процессе, к температуре, при которой происходит теплопередача, т.е. Q/T, называется приведённой теплотой.

Алгебраическая сумма приведённыхтеплот для обратимого цикла Карно равна нулю.

Функция, характеризующая направление протекания самопроизвольных процессов в замкнутой термодинамической системе, называется энтропией: .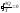

Каждому состоянию тела соответствует одно определённое значение энтропии. Поэтому энтропия является однозначной функцией состояния.

35. Реальные газы.

Силы взаимодействия, проявляющиеся на расстоянии порядка 10^-9-10^-10 м, называют ван-дер-ваальсовыми.

Внутренняя энергия реального газа.

Внутренняя энергия реального газа определяется суммой потенциальной энергии взаимодействия молекул и кинетической энергии их движения.

Так как потенциальная энергия взаимодействия молекул зависит от их взаимного расположения, то она должна изменяться при изменении объёма газа. Потенциальную энергию взаимодействия молекул 1 моль газа можно вычислить по формуле: Eп=интг(r_внdV), где r_вн=-a/V² – добавочное внутренне давление, входящее в уравнение Ван-дер-Ваальса.

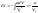
Эта энергия имеет отрицательный знак, т.к. молекулярные силы, создающие внутреннее давление, являются силами притяжения.

Использую закон Джоуля, можно вычислить внутреннюю энергию реального газа: U=C_VT-a/V_M – для одного моля.

Внутренняя энергия n моль газа определяется по формуле U=nC_VT-a¢/V, где a¢=n²a, V=nV_M.

Внутренняя энергия реального газа зависит как от температуры, так и от объёма.

https://studfiles.net/preview/5616181/page:10/

1.Кинематика материальной точки.

Материальная точка –тело, размерами которого в данной задаче можно пренебречь.

Абсолютно твёрдое тело –система материальных точек, расстояние между которыми не изменяется в процессе движения.

Движение тела называется поступательным, если любая прямая, соединяющая две любые его точки, остается всё время параллельной самой себе.

При вращательном движении твёрдого тела все его точки описывают окружности, центры которых лежат на одной прямой – оси вращения.

Радиус-вектор, скорость и ускорение.

Положение точки может быть задано радиус-вектором r, проведённый из начала системы координат к точке. Радиус вектор зависит от времени r=r(t). Векторному уравнению эквивалентна система скалярных уравнений: x=x(t), y=y(t), z=z(t). Называются уравнениями движения материальной точки.

Длина участка траектории АВ пройденного материальной точкой за промежуток Dt, называется длиной пути Ds и является скалярной функцией времени.

На участке АВ вектор средней М скорости равен <V>=Dr/Dt и направлен вдоль хорды АВ в ту же сторону, что и вектор перемещения Dr. Скорость в точке А (мгновенная скорость) V=lim(Dt®0)(Dr/Dt)=dr/dt. Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Так как модуль вектора Dr равен длине ds малого участка траектории, то u=|V|=ds/dt, т.е. модуль скорости равен первой производной по времени.

Быстрота изменения скорости характеризуется вектором ускорения а.

Среднее ускорение – отношение изменения скорости DV к промежутку времени Dt, в течение которого произошло это изменение: <a>=DV/Dt. Вектор среднего ускорения совпадает по направлению с вектором изменения скорости.

Мгновенное ускорение a=lim(Dt®0)(DV/Dt)=dV/dt.

Ускорение – векторная величина, равная первой производной скорости по времени.

Нормальная и тангенциальная составляющая.

Вектор DV можно разложить на две составляющие: DVt - вдоль касательной, DVn – вдоль нормали. DVt определяет изменение скорости по модулю, DVn – по направлению за промежуток Dt: a=lim(Dt®0)(DV/Dt)=lim(Dt®0)(DVt/Dt)+lim(Dt®0)(DVn/Dt)=at+an.Модуль тангенциального ускорения равен производной модуля скорости по времени: at=du/dt.

Модуль нормального ускорения: an=u²/R, где R – радиус кривизны траектории.

Радиус кривизны представляет собой радиус окружности, которая сливается в данном месте с кривой на бесконечно малом её участке. Центром такой окружности называется центром кривизны для данной точки кривой. Система отсчёта -совокупность системы координат и часов, связанных с телом отсчёта.Чаще используют декартову с.к. Тело отсчёта-произвольно выбранное тело относительно которого определяется положение другого тела.движение мат. точк и полносью определено в пространстве,если декартовы координаты заданы в завмсимости от времени r=r(t)

2.Кинематика вращательного движения. Угловые скорость и ускорение.

Пусть радиус окружности, описываемой некоторой точкой, равен r, а её линейное перемещение – ds. Тогда угловое перемещение dj (угол поворота радиус-вектора) dj=ds/r.

Угловая скорость равна первой производной от угла поворота радиус-вектора по времени: w=lim(Dt®0)(Dj/Dt)=dj/dt. Если направление вращения винта совпадает с вращением тела, то конец винта укажет направление вектора w.

Время одного полного поворота тела вокруг оси вращения называют периодом обращенияT, а величину n, обратную периоду, -частотой. w=2p/T=2pn.

Единица угловой скорости – рад/с.

Быстрота изменения угловой скорости характеризуется угловым ускорением.

Угловое ускорение равно первой производной от угловой скорости по времени или второй производной от угла поворота радиус-вектора по времени: e=lim(Dt®0)(Dw/Dt)=dw/dt=d²w/dt².

Угловое ускорение также является векторной величиной. При ускоренном вращении e совпадает с вектором w, при замедленном вращении e противоположно w.

Единица углового ускорения – рад/с².

https://studfiles.net/preview/5616181/