Вопрос 2. Понятие определенного интеграла как предела интегральной суммы

Решение рассмотренных выше задач сводилось к отысканию предела суммы специального вида при неограниченном возрастании числа отрезков деления и стягивания каждого из них в точку.

Изучим этот процесс независимо от конкретного содержания той или иной задачи.

Пусть функция y = f(x) определена на отрезке [a;b], где a < b. Выполним следующие действия.

1. Разобьем отрезок [a;b] точками a = x₀ < x₁ < … < x_n‒1 < x_n = b на n частичных отрезков [x_i‒1;x_i] с длинами Δx_i = x_i ‒ x_i‒1, где i = 1,2,…,n.

2. В каждом частичном отрезке [x_i‒1;x_i] выберем произвольную точку c_i и вычислим значение функции в ней f(c_i).

3. Найдем произведения f(c_i)Δx_i, i = 1,2,…,n.

4. Составим сумму S_n всех таких произведений:

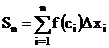. (3)

Сумма вида (3) называется интегральной суммойфункции y = f(x) на отрезке [a;b], соответствующей данному разбиению отрезка [a;b] на частичные отрезки [x_i‒1;x_i] и данному выбору промежуточных точек c_i в них.

Пусть 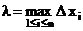- длина наибольшего частичного отрезка разбиения.

5. Найдем предел интегральной суммы (3) при l®0 (т.е. при n ® ¥).

О.2.1. Если существует конечный предел I интегральной суммы (3) при l®0, который не зависит от способа разбиения отрезка [a;b] на частичные отрезки [x_i‒1;x_i] и от выбора в них точек c_i, то этот предел называется определенным интегралом от функции y = f(x) на отрезке [a;b] и обозначается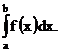

По определению

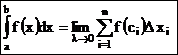. (4)

Числа a и b называются соответственно нижним и верхним пределами интегрирования, функция f(x) - подынтегральной функцией, f(x)dx - подынтегральным выражением, x - переменной интегрирования, отрезок [a;b] - областью (отрезком) интегрирования.

О.2.2.Функция y = f(x), для которой на отрезке [a;b] существует определенный интеграл 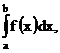называется интегрируемойна этом отрезке.

Данное аналитическое определение определенного интеграла впервые было сформулировано для непрерывных функций в 1823 г. Коши. Позднее Риман показал, что определение, данное Коши, применимо к более широкому классу функций. Это позволило ему впервые высказать в общей форме определение интеграла и установить условия его существования. Поэтому интеграл (4) называют интегралом Римана. Обозначение интеграла 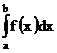было введено Фурье.

Замечание

Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы – существенно различные понятия: òf(x)dx - совокупность функций, а 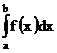- определенное число.

Вопрос 3. Необходимое и достаточное условие существования определенного интеграла

Т.3.1. (необходимое условие существования определенного интеграла)

Если функция y = f(x) интегрируема на отрезке [a;b], то она ограничена на этом отрезке.

Замечание

Обратная теорема неверна, т.е. из ограниченности функции y = f(x) еще не следует ее интегрируемость.

Пример. Рассмотрим функцию Дирихле, которая имеет широкое применение в технических приложениях:

Для функции Дирихле:

1. Если c_i - рациональное число, то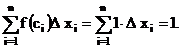

2. Если c_i - иррациональное число, то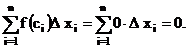

Очевидно, что для функции Дирихле предел интегральной суммы (3) не существует, следовательно, не существует и определенный интеграл от данной функции. При этом функция Дирихле ограничена.