Электронная теория дисперсии света

Из макроскопической электромагнитной теории Максвелла следует, что абсолют­ный показатель преломления среды

n=Öem,

где e — диэлектрическая проницаемость среды, m — магнитная проницаемость. В оптической области спектра для всех веществ m»1 поэтому

n=Öe. (186.1)

Из формулы (186.1) выявляются не­которые противоречия с опытом: величина n, являясь переменной (см. § 185), остает­ся в то же время равной определенной постоянной Öe. Кроме того, значения n, получаемые из этого выражения, не со­гласуются с опытными значениями. Труд­ности объяснения дисперсии света с точки зрения электромагнитной теории Максвел­ла устраняются электронной теорией Лоренца. В теории Лоренца дисперсия света рассматривается как результат взаимо-

действия электромагнитных волн с заря­женными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнит­ном поле волны.

Применим электронную теорию дис­персии света для однородного диэлектри­ка, предположив формально, что диспер­сия света является следствием зависимо­сти e от частоты w световых волн. Диэлектрическая проницаемость вещест­ва по определению (см. (88.6) и (88.2)) равна

e=1+c=1+Р/(e₀E),

где c — диэлектрическая восприимчивость среды, e₀ — электрическая постоянная, P — мгновенное значение поляризованности. Следовательно,

n²=1+Р/(e₀E), (186.2)

т. е. зависит от Р. В данном случае основ­ное значение имеет электронная поляриза­ция, т. е. вынужденные колебания элек­тронов под действием электрической со­ставляющей поля волны, так как для ориентационной поляризации молекул частота колебаний в световой волне очень высока (v»10¹⁵ Гц).

В первом приближении можно считать, что вынужденные колебания совершают только внешние, наиболее слабо связан­ные с ядром электроны — оптические электроны.Для простоты рассмотрим ко­лебания только одного оптического элек­трона. Наведенный дипольный момент электрона, совершающего вынужденные колебания, равен р=ех, где е — заряд электрона, х — смещение электрона под действием электрического поля световой волны. Если концентрация атомов в ди­электрике равна по, то мгновенное значе­ние поляризованности

Р=n₀p=n₀ех. (186.3)

Из (186.2) и (186.3) получим

n²=1+n₀ех/(e₀E). (186.4)

Следовательно, задача сводится к опреде­лению смещения х электрона под действи­ем внешнего поля Е. Поле световой волны

будем считать функцией частоты w, т. е. изменяющимся по гармоническому закону: E=E₀coswt.

Уравнение вынужденных колебаний электрона (см. § 147) для простейшего случая (без учета силы сопротивления, обусловливающей поглощение энергии па­дающей волны) запишется в виде

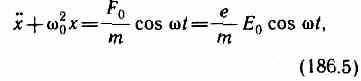
где F₀=eE₀— амплитудное значение си­лы, действующей на электрон со стороны поля волны, w0=Ök/m — собственная частота колебаний электрона, m — масса электрона. Решив уравнение (186.5), най­дем e=n² в зависимости от констант ато­ма (е, т, w₀) и частоты w внешнего поля, т. е. решим задачу дисперсии.

Решение уравнения (186.5) можно за­писать в виде

в чем легко убедиться подстановкой (см. (147.8)). Подставляя (186.6) и (186.7) в (186.4), получим

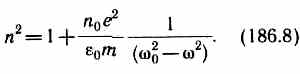
Если в веществе имеются различные за­ряды e_i, совершающие вынужденные коле­бания с различными собственными часто­тами w_0i, то

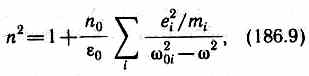
где m_i — масса i-ro заряда.

Из выражений (186.8) и (186.9) вы­текает, что показатель преломления n за­висит от частоты w внешнего поля, т. е. по­лученные зависимости действительно под­тверждают явление дисперсии света, хотя и при указанных выше допущениях, кото-

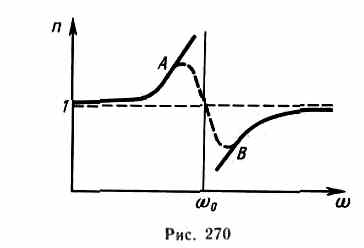
рые в дальнейшем надо устранить. Из выражений (186.8) и (186.9) следует, что в области от w=0 до w=w₀n² больше еди­ницы и возрастает с увеличением со (нор­мальная дисперсия); при w=w₀ n²= ±¥; в области от w=w₀ до w=¥ n² меньше единицы и возрастает от -¥ до 1 (нормальная дисперсия). График за­висимости и от со представлен на рис. 270. Подобное поведение n вблизи собствен­ной частоты w₀ получилось в результате допущения об отсутствии сил сопротив­ления при колебаниях электронов. Если принять в расчет и это обстоятельство, то график функции n (w) вблизи w₀ за­дается штриховой линией АВ. Область АВ — область аномальной дисперсии (n убывает при возрастании w), осталь­ные участки зависимости n от w опи­сывают нормальную дисперсию (n воз­растает с возрастанием со).

Советскому физику Д. С. Рожде­ственскому (1876—1940) принадлежит классическая работа по изучению ано­мальной дисперсии в парах натрия. Он разработал интерференционный метод для очень точного измерения показателя пре­ломления паров и экспериментально по­казал, что формула (186.9) правильно ха­рактеризует зависимость и отсо, а также ввел в нее поправку, учитывающую кван­товые свойства света и атомов.

Дисперсия света