Энергетическое строение атома водорода
В Таблице 4 представлены номера орбит, их радиусы и соответствующие им уровни энергии электрона в атоме водорода в двух основных энергетических состояниях, что составляет основу энергетического строения этого атома. В данную таблицу включены 19 орбит первого основного энергетического состояния и 37 первых орбит второго основного энергетического состояния. При этом все нечетные орбиты второго основного энергетического состояния совпадают с орбитами первого основного энергетического состояния. Кроме того, некоторые уровни энергии в обоих энергетических состояниях электрона совпадают. Такое совпадение энергетических состояний приводит к возникновению близких и практически совпадающих спектральных линий, дублетов.
В Таблице 5 представлена угловая скорость электрона на каждой из возможных орбит в обоих энергетических состояниях. Угловая скорость на n-ной орбите для первого энергетического состояния электрона определялась по формуле:
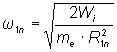 , , | (24) |
где Rn − радиус n-ной орбиты. Во втором энергетическом состоянии энергия ионизации в 4 раза меньше и орбиты расположены чаще:
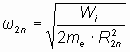 . . | (25) |
В Таблице 6 представлены возможные переходы электрона в пределах первого основного энергетического состояния, величины разности энергии и соответствующая им длина волны электромагнитного излучения для первых 18 спектральных линий вакуумной области спектра, известных, как уже упоминалось, под названием спектральной серии Лаймона.
Таблица 4. Радиусы орбит и уровни энергии электрона в атоме водорода
| 1-е основное энергетическое состояние электрона | 2-е основное энергетическое состояние электрона | ||||
| № орбиты, n | Радиус орбиты, ×10 -10 м | Энергия электрона на данной орбите в состоянии W1.n (эВ) | № орбиты, 2n-1 | Радиус орбиты, ×10 -10 м | Энергия электрона на данной орбите в состоянии W2.2n-1 (эВ) |
| 0.529365 | W1.1 13.60097 | 0.529365 | W2.1 3.40025 | ||
| 1.191071 | W2.2 1.51122 | ||||
| 2.117458 | W1.2 3.40025 | 2.117458 | W2.3 0.850062 | ||
| 3.308531 | W2.4 0.544039 | ||||
| 4.764281 | W1.3 1.51122 | 4.764281 | W2.5 0.377805 | ||
| 6.484721 | W2.6 0.277571 | ||||
| 8.469834 | W1.4 0.850062 | 8.469834 | W2.7 0.212515 | ||
| 10.71964 | W2.8 0.167913 | ||||
| 13.23413 | W1.5 0.54404 | 13.23413 | W2.9 0.13601 | ||
| 16.01329 | W2.10 0.112405 | ||||
| 19.05714 | W1.6 0.377806 | 19.05714 | W2.11 0.0944511 | ||
| 22.36567 | W2.12 0.0804791 | ||||
| 25.93889 | W1.7 0.277571 | 25.93889 | W2.13 0.0693927 | ||
| 29.77678 | W2.14 0.0604488 | ||||
| 33.87936 | W1.8 0.212516 | 33.87936 | W2.15 0.0531288 | ||
| 38.24662 | W2.16 0.0470622 | ||||
| 42.87857 | W1.9 0.167914 | 42.87857 | W2.17 0.0419783 | ||
| 47.77519 | W2.18 0.0376758 | ||||
| 52.93646 | W1.10 0.13601 | 52.93646 | W2.19 0.0340025 | ||
| 58.36249 | W2.20 0.0308412 | ||||
| 64.05317 | W1.11 0.112405 | 64.05317 | W2.21 0.0281012 | ||
| 70.00852 | W2.22 0.0257107 | ||||
| 76.22856 | W1.12 0.0944514 | 76.22856 | W2.23 0.0236128 | ||
| 82.71328 | W2.24 0.0217616 | ||||
| 89.46269 | W1.13 0.0804793 | 89.46269 | W2.25 0.0201198 | ||
| 96.47677 | W2.26 0.018657 | ||||
| 103.7555 | W1.14 0.0693929 | 103.7555 | W2.27 0.0173482 | ||
| 111.2990 | W2.28 0.01611724 | ||||
| 119.1071 | W1.15 0.0604489 | 119.1071 | W2.29 0.0151122 | ||
| 127.1799 | W2.30 0.0141529 | ||||
| 135.5174 | W1.16 0.0531289 | 135.5174 | W2.31 0.0132822 | ||
| 144.1196 | W2.32 0.0124894 | ||||
| 152.9865 | W1.17 0.0470623 | 152.9865 | W2.33 0.0117655 | ||
| 162.1180 | W2.34 0.0111028 | ||||
| 171.5143 | W1.18 0.0419784 | 171.5143 | W2.35 0.0104946 | ||
| 181.1752 | W2.36 0.0093497 | ||||
| 191.1008 | W1.19 0.0376759 | 191.1008 | W2.37 0.0094190 |
Таблица 5. Радиусы орбит и угловая скорость электрона в атоме водорода
| 1-е основное энергетическое состояние электрона | 2-е основное энергетическое состояние электрона | ||||
| № орбиты, n | Радиус орбиты, ×10 -10 м | Угловая скорость электрона, ×10 15 рад/с | № орбиты, 2n-1 | Радиус орбиты, ×10 -10 м | Угловая скорость электрона, ×10 15 рад/с |
| 0.529365 | 41.3193 | 0.529365 | 20.6597 | ||
| 1.191071 | 9.18209 | ||||
| 2.117458 | 10.3299 | 2.117458 | 5.16493 | ||
| 3.308531 | 3.30555 | ||||
| 4.764281 | 4.59105 | 4.764281 | 2.29552 | ||
| 6.484721 | 1.68651 | ||||
| 8.469834 | 2.58246 | 8.469834 | 1.29123 | ||
| 10.71964 | 1.02023 | ||||
| 13.23413 | 1.65278 | 13.23413 | 0.826388 | ||
| 16.01329 | 0.62965 | ||||
| 19.05714 | 1.14776 | 19.05714 | 0.573881 | ||
| 22.36567 | 0.488987 | ||||
| 25.93889 | 0.843253 | 25.93889 | 0.421626 | ||
| 29.77678 | 0.367284 | ||||
| 33.87936 | 0.645616 | 33.87936 | 0.322808 | ||
| 38.24662 | 0.285947 | ||||
| 42.87857 | 0.510116 | 42.87857 | 0.255058 | ||
| 47.77519 | 0.228916 | ||||
| 52.93646 | 0.413194 | 52.93646 | 0.206597 | ||
| 58.36249 | 0.18739 | ||||
| 64.05317 | 0.341483 | 64.05317 | 0.170741 | ||
| 70.00852 | 0.156217 | ||||
| 76.22856 | 0.28694 | 76.22856 | 0.14347 | ||
| 82.71328 | 0.132222 | ||||
| 89.46269 | 0.244493 | 89.46269 | 0.122247 | ||
| 96.47677 | 0.113359 | ||||
| 103.7555 | 0.210813 | 103.7555 | 0.105407 | ||
| 111.2990 | 0.0982625 | ||||
| 119.1071 | 0.183642 | 119.1071 | 0.0918209 | ||
| 127.1799 | 0.0859925 | ||||
| 135.5174 | 0.161404 | 135.5174 | 0.080702 | ||
| 144.1196 | 0.0774983 | ||||
| 152.9865 | 0.142974 | 152.9865 | 0.0714868 | ||
| 162.1180 | 0.0674603 | ||||
| 171.5143 | 0.127529 | 171.5143 | 0.0637645 | ||
| 181.1752 | 0.0603643 | ||||
| 191.1008 | 0.114458 | 191.1008 | 0.0572291 |
Длина волны в спектральной серии Лаймона определялась по формуле, связывающей энергию электрона с его моментом импульса:
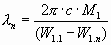 , , | (26) |
В этой формуле введен пересчетный коэффициент 2, учитывающий то, что разность механической энергии состояния электрона в атоме распределяется в электромагнитной волне на две равных составляющих, в соответствии со структурой электромагнитной волны.
Так как во втором энергетическом состоянии и момент импульса, и энергия состояния в четыре раза меньше, то определить длину волны и во второй спектральной серии атома водорода (Таблица 7) можно по этой же формуле (26).
Если брать из Таблицы 5 значения угловых скоростей электрона, то также можно найти длины волн соответствующих спектральных линий по формуле, связывающей длину волны с частотой электромагнитной волны. Однако здесь надо обратить внимание на то, что разность угловых скоростей вращения электрона на орбите может несовпадать с частотой электромагнитной волны. При простом соотношении энергии состояний угловые скорости и частоты могут быть кратны. Поэтому в формулу для нахождения длины электромагнитной волны по разности угловой скорости электрона, переходящего на различные орбиты в пределах одного и того же основного энергетического состояния, необходимо ввести коэффициент кратности, k:
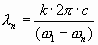 . . | (27) |
В первом энергетическом состоянии k=2, а во втором энергетическом состоянии k=4.
Причина несоответствия разности угловых скоростей вращения электрона и частоты электромагнитной волны при энергетическом подходе понятна и заключается в перераспределении механической энергии на две составляющие электромагнитные волны, каждая из которых в результате имеет в два раза более низкую частоту колебаний.
Той же самой причиной объясняется появление коэффициента k=2 при расчете длины волны в первом основном энергетическом состоянии по формуле (27).
Почему же при применении формулы (27) во втором энергетическом состоянии коэффициент кратности необходимо еще раз удвоить? Причина этого связана с соотношением радиусов орбит электрона, удовлетворяющим равенству момента импульса электрона во втором основном энергетическом состоянии. Проще говоря, угловая частота вращения электрона во втором энергетическом состоянии, при одном и том же моменте импульса электрона, в два раза ниже. Поэтому эквивалентная частота электромагнитной волны, излучаемой во втором энергетическом состоянии, также будет в два раза ниже, что удваивает коэффициент кратности, k. В первом основном энергетическом состоянии такого удвоения нет, так как момент импульса электрона кратен целому числу оборотов электрона вокруг ядра.
Таблица 6. Переходы в пределах первого основного энергетического состояния электрона и соответствующая им длина волны электромагнитного излучения первых 18 спектральных линий (серия Лаймона).
| № | Переход между энергетическими состояниями | Величина разности энергии состояний (эВ) | Длина волны, ×10 -10 м |
| W1.1- W1.2 | 10.20072 | 1215.672 | |
| W1.1- W1.3 | 12.08975 | 1025.722 | |
| W1.1- W1.4 | 12.750908 | 972.537 | |
| W1.1- W1.5 | 13.05693 | 949.743 | |
| W1.1- W1.6 | 13.223164 | 937.803 | |
| W1.1- W1.7 | 13.323399 | 930.748 | |
| W1.1- W1.8 | 13.388454 | 926.225 | |
| W1.1- W1.9 | 13.433056 | 923.150 | |
| W1.1- W1.10 | 13.46496 | 920.963 | |
| W1.1- W1.11 | 13.488565 | 919.351 | |
| W1.1- W1.12 | 13.5065186 | 918.129 | |
| W1.1- W1.13 | 13.5204907 | 917.180 | |
| W1.1- W1.14 | 13.5315771 | 916.429 | |
| W1.1- W1.15 | 13.5405211 | 915.823 | |
| W1.1- W1.16 | 13.5478411 | 915.329 | |
| W1.1- W1.17 | 13.5539077 | 914.919 | |
| W1.1- W1.18 | 13.5589916 | 914.576 | |
| W1.1- W1.19 | 13.5632941 | 914.286 |
Все длины волн спектральных линий из Таблицы 6, построенной на основе энергетического спектра электрона, данного в Таблице 4 для первого основного энергетического состояния, точно соответствуют длинам волн спектральной серии Лаймона и могут быть получены из выведенной ранее формулы (14) для первого основного энергетического состояния электрона в атоме водорода.
Формула (14) позволяет вычислить и другие возможные спектральные линии этой серии, но эти потенциальные спектральные линии отсутствуют в имеющихся справочниках. В отличие от первого основного энергетического состояния, во всех остальных энергетических состояниях электрон не может быть сколь угодно долго. Электрон всегда стремится перейти из этих состояний в одно из двух основных своих энергетических состояний, W1 и W2, а из W2 – в состояние с наименьшей энергией W1.
Все длины волн спектральных линий, помещенные в Таблице 7, построенной на основе энергетического спектра электрона для второго основного энергетического состояния электрона по данным Таблицы 4, соответствуют длинам волн спектральной серии Бальмера и могут быть получены из выведенной ранее формулы (18) для второго основного энергетического состояния электрона в атоме водорода.
Таблица 7. Переходы в пределах второго основного энергетического состояния электрона и соответствующая им длина волны электромагнитного излучения первых 30 спектральных линий (серия Бальмера).
| № пп | Переход между энергетическими состояниями W2.1- W2.(n+1) | Разность энергии состояний (эВ) | Длина волны, λвак ×10 -10 м (вакуум) | Попр. (Рис.) Δλ×10 -10 м | λ вычис- ленное, ×10 -10 м (воздух) | λ изме- ренное, ×10 -10 м (воздух) | δλ |
| W2.1- W2.2 | 1.88903 | 6564.60 | -1.82 | 6562.78 | 6562.82* | -0.04 | |
| W2.1- W2.3 | 2.550188 | 4862.67 | -1.35 | 4861.32 | 4861.33 | -0.01 | |
| W2.1- W2.4 | 2.856211 | 4341.67 | -1.22 | 4340.45 | 4340.47 | -0.02 | |
| W2.1- W2.5 | 3.022445 | 4102.88 | -1.16 | 4101.72 | 4101.74 | -0.02 | |
| W2.1- W2.6 | 3.122679 | 3971.18 | -1.12 | 3970.06 | 3970.07 | -0.01 | |
| W2.1- W2.7 | 3.187735 | 3890.14 | -1.10 | 3889.04 | 3889.05 | -0.01 | |
| W2.1- W2.8 | 3.232337 | 3836.46 | -1.08 | 3835.38 | 3835.39 | -0.01 | |
| W2.1- W2.9 | 3.26424 | 3798.96 | -1.07 | 3797.89 | 3797.90 | -0.01 | |
| W2.1- W2.10 | 3.287845 | 3771.69 | -1.06 | 3770.63 | 3770.63 | ||
| W2.1- W2.11 | 3.3057989 | 3751.20 | -1.06 | 3750.14 | 3750.15 | -0.01 | |
| W2.1- W2.12 | 3.3197709 | 3735.42 | -1.06 | 3734.36 | 3734.37 | -0.01 | |
| W2.1- W2.13 | 3.3308573 | 3722.98 | -1.05 | 3721.94 | 3721.94 | ||
| W2.1- W2.14 | 3.3398012 | 3713.01 | -1.05 | 3711.96 | 3711.97 | -0.01 | |
| W2.1- W2.15 | 3.3471212 | 3704.89 | -1.04 | 3703.85 | 3703.86 | -0.01 | |
| W2.1- W2.16 | 3.3531878 | 3698.19 | -1.04 | 3697.15 | 3697.15 | ||
| W2.1- W2.17 | 3.3582717 | 3692.59 | -1.04 | 3691.55 | 3691.56 | -0.01 | |
| W2.1- W2.18 | 3.3625742 | 3687.87 | -1.04 | 3686.83 | 3686.83 | ||
| W2.1- W2.19 | 3.3662475 | 3683.84 | -1.04 | 3682.80 | 3682.81 | -0.01 | |
| W2.1- W2.20 | 3.3694088 | 3680.39 | -1.04 | 3679.35 | 3679.36 | -0.01 | |
| W2.1- W2.21 | 3.3721488 | 3677.40 | -1.04 | 3676.36 | 3676.36 | ||
| W2.1- W2.22 | 3.3745393 | 3674.79 | -1.04 | 3673.75 | 3673.76 | -0.01 | |
| W2.1- W2.23 | 3.3766372 | 3672.51 | -1.04 | 3671.47 | 3671.48 | -0.01 | |
| W2.1- W2.24 | 3.3784884 | 3670.50 | -1.04 | 3669.46 | 3669.47 | -0.01 | |
| W2.1- W2.25 | 3.3801302 | 3668.71 | -1.04 | 3667.67 | 3667.68 | -0.01 | |
| W2.1- W2.26 | 3.381593 | 3667.13 | -1.03 | 3666.10 | 3666.10 | ||
| W2.1- W2.27 | 3.3829018 | 3665.71 | -1.03 | 3664.68 | 3664.68 | ||
| W2.1- W2.28 | 3.38413276 | 3664.37 | -1.03 | 3663.34 | 3663.41 | -0.07 | |
| W2.1- W2.29 | 3.3851378 | 3663.29 | -1.03 | 3662.26 | 3662.26 | ||
| W2.1- W2.30 | 3.3860971 | 3662.25 | -1.03 | 3661.22 | 3661.22 | ||
| W2.1- W2.31 | 3.3869678 | 3661.31 | -1.03 | 3660.28 | - | - |
Таблица 8. Переходы между основными состояниями электрона и соответствующая им длина волны электромагнитного излучения.
| № пп | Переход между энергетическими уровнями: | Величина разности энергетических состояний (эВ) | Длина волны в вакууме, λ×10 -10 м | Поправка на изменение λ в воздухе, Δλ (×10 -10 м) | Длина волны в воздухе, λ×10 -10 м |
| W1.1- W2.1 | 10.20075 | 1215.67* | |||
| W1.1- W2.2 | 12.08978 | 1025.72* | |||
| W1.1- W2.3 | 12.75094 | 972.534* | |||
| W1.1- W2.4 | 13.05698 | 949.739* | |||
| W1.1- W2.5 | 13.223194 | 937.80* | |||
| W1.1- W2.6 | 13.323429 | 930.735* | |||
| W1.1- W2.7 | 13.388484 | 926.223* | |||
| W1.1- W2.8 | 13.433086 | 923.147* | |||
| W1.1- W2.9 | 13.46499 | 920.96* | |||
| W1.1- W2.10 | 13.488595 | 919.348* | |||
| W1.1- W2.11 | 13.5065486 | 918.126* | |||
| W1.1- W2.12 | 13.520521 | 917.177* | |||
| W1.1- W2.13 | 13.5316071 | 916.426* | |||
| W1.1- W2.14 | 13.5405511 | 915.821* | |||
| W1.1- W2.15 | 13.5478711 | 915.326* | |||
| W1.1- W2.16 | 13.5539377 | 914.916* | |||
| W1.1- W2.17 | 13.5590216 | 914.573* | |||
| W1.1- W2.18 | 13.5633241 | 914.283** | |||
| W1.2- W2.2 | 1.88903 | 6564.6 * | -1.81 | 6562.79 | |
| W1.2- W2.3 | 2.550188 | 4862.67* | |||
| W1.2- W2.4 | 2.85621 | 4341.67* | |||
| W1.2- W2.5 | 6.022444 | 2059.08** | |||
| W1.3- W2.3 | 0.661158 | 18756.1 | (-5) | 18751.1 | |
| W1.3- W2.4 | 0.96718 | 12821.5 | -3.5 | ||
| W1.3- W2.5 | 1.133414 | 10941.0 | -2 | ||
| W1.3- W2.6 | 1.233649 | 10052.1 | -2.75 | 10049.25 | |
| W1.3- W2.7 | 1.298704 | 9548.53 | -2.63 | 9545.9 | |
| W1.3- W2.8 | 1.343306 | 9231.49 | -2.5 | 9228.99 | |
| W1.3- W2.9 | 1.37521 | 9017.33 | -2.47 | 9014.86 | |
| W1.3- W2.10 | 1.398815 | 8865.16 | -2.43 | 8862.73 | |
| W1.3- W2.11 | 1.4167686 | 8752.82** | |||
| W1.4- W2.4 | 0.306022 | 40522.3 | (-10.9) | 40511.4 | |
| W1.4- W2.5 | 0.472256 | 26258.5 | (-7.2) | 26251.3 | |
| W1.4- W2.6 | 0.572491 | 21661.0** | |||
| W1.5- W2.5 | 0.166234 | 74598.0 | |||
| W1.5- W2.6 | 0.266469 | 46537.2** | |||
| W1.6- W2.6 | 0.100235 | (-32) | |||
| W1.6- W2.7 | 0.16529 | (-20) | |||
| W1.6- W2.8 | 0.209892 | 59081.4** | |||
| W1.7- W2.7 | 0.065055 | (-50) | |||
| W1.7- W2.8 | 0.109657 | (-29) |
*) – данная спектральная линия имеется в 1-й или 2-й основной серии;
**) – спектральная линия с такой длиной волны отсутствует в справочниках [1, 5].
Восемнадцать первых спектральных линий в Таблице 8 совпадают с соответствующими спектральными линиями серии Лаймона в Таблице 6.
Спектральные линии под номерами 19 – 21 в Таблице 8 совпадают с первыми тремя спектральными линиями серии Бальмера (Таблица 7).
Восемь спектральных линий под номерами 23 – 30 в Таблице 8 составляют третью спектральную серию, называемую серией Пашена.
Спектральные линии под номерами 32 и 33 в Таблице 8 составляют четвертую «спектральную серию» атома водорода.
Спектральная линия под номером 35 в Таблице 8 представляет пятую «спектральную серию» атома водорода.
Спектральные линии под номерами 37 и 38 в Таблице 8 составляют шестую «спектральную серию» атома водорода.
Спектральные линии под номерами 40 и 41 в Таблице 8 составляют седьмую, заключительную «серию» известных спектральных линий атома водорода.
Все спектральные линии, входящие в серию Лаймона, могут быть получены двумя способами:
а) при переходе электрона с любой орбиты на первую в первом основном энергетическом состоянии (без изменения состояния собственного момента импульса электрона);
б) при переходе электрона с любой орбиты второго основного состояния на первую орбиту первого основного энергетического состояния (с изменением величины и направления собственного момента импульса электрона).
Аналогично спектральным линиям, входящие в серию Лаймона, первые три спектральные линии серии Бальмера могут быть получены этими же двумя способами (без изменения собственного момента импульса электрона и с изменением собственного момента импульса электрона). На языке «квантовой физики» такие состояния называются «дважды вырожденными», хотя никакого «вырождения» здесь нет, – просто электрон может перейти из одних энергетических состояний в другие, получив или отдав при этом практически равную порцию электромагнитной энергии. Небольшая разница в энергии состояний определяет тонкую структуру этих линий.
То есть все спектральные линии серии Лаймона и три первые спектральные линии серии Бальмера принципиально являются двойными спектральными линиями, дублетами, даже если тонкая структура некоторых из этих спектральных линий до сих пор не обнаружена.
Спектральные линии, входящие в 3-ю – 7-ю «серии», получаются только при переходах с изменением состояния собственного момента импульса, то есть при переходах между двумя основными энергетическими состояниями электрона.
На Рис. 3. показана вычисленная поправка на изменение длины волны в воздухе, полученная из расчетной и измеренной длин волн для той части спектра, где автор не нашел экспериментальных данных для сопоставления, как это было сделано для спектральных линий серии Бальмера и других спектральных линий, входящих в диапазон длин волн, показанный на Рис. 2. Вычисленная поправка, в отличие от поправки, взятой из эксперимента, в Таблице 8 дана в круглых скобках.
На Рис. 4 графически показана энергетическая структура атома водорода, соответствующая данным Таблицы 4, и допустимые энергетические переходы в этом атоме, соответствующие данным, помещенным в Таблицы 6 – 8.
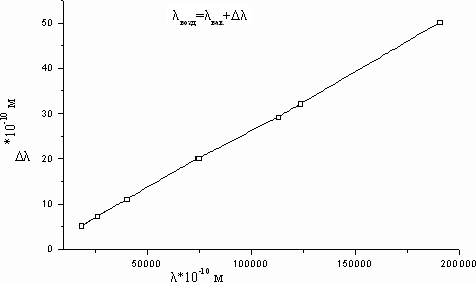
Рис. 3. Поправка на изменение длины волны в воздухе, вычисленная по данным Таблицы 7 (эти расчетные данные в Таблице 7 приведены в скобках).
Энергетические переходы внутри первого основного энергетического состояния, W1.1 – W1.n, составляют спектральную серию Лаймона (Таблица 6).
Энергетические переходы внутри второго основного энергетического состояния, W2.1 – W2.n, составляют спектральную серию Бальмера (Таблица 7). Энергетические переходы между первой орбитой первого основного энергетического состояния и всеми орбитами второго основного энергетического состояния, W1.1 – W2.n, полностью дублируют все известные линии спектральной серии Лаймона (Таблица 8).
Из Рис. 4. следует, что электрон в атоме на первой орбите и на половине последующих орбит может находиться в двух различных энергетических состояниях, отличающихся как величиной энергии, так и величиной и направлением собственного момента импульса.
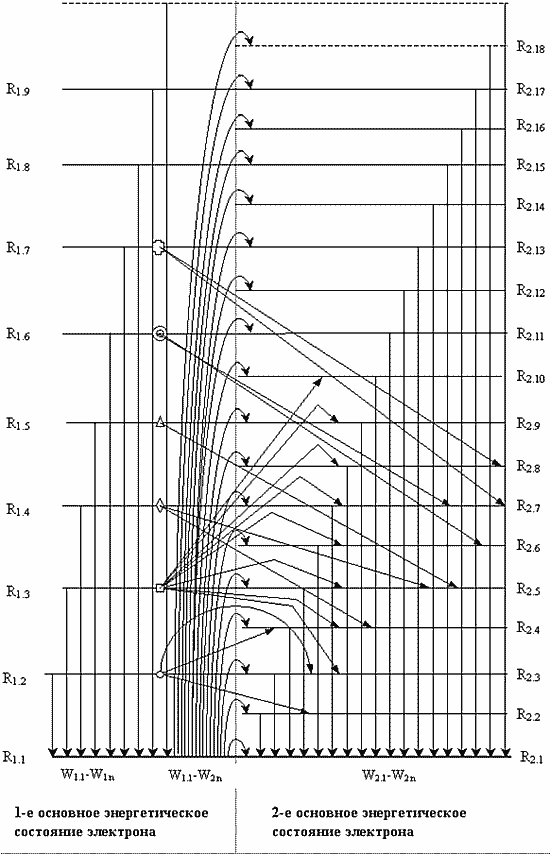
Рис. 4. Структура энергетических переходов атома водорода.
Условное расположение орбит атома водорода на Рис. 4 показано без соблюдения масштаба, причем представлены не все, а только ближайшие к ядру атома орбиты электрона в обоих основных энергетических состояниях. Одностороннее направление стрелок при энергетических переходах показано условно, так как переходы могут осуществляться в обоих направлениях (поглощение и излучение электромагнитной энергии).
Энергетические переходы между второй орбитой первого основного энергетического состояния (обозначено кружком) и второй, третьей и четвертой орбитами второго основного энергетического состояния, W1.2 – W2.2, W1.2 – W2.3 и W1.2 – W2.4 дублируют три первые линии спектральной серии Бальмера. Энергетические переходы между третьей орбитой первого основного энергетического состояния (обозначено квадратом) и третьей – десятой орбитами второго основного энергетического состояния, от W1.3 – W2.3 до W1.3 – W2.10 составляют так называемую спектральную серию Пашена.
С четвертой орбиты первого основного энергетического состояния (обозначена ромбом) возможен переход только на четвертую и пятую орбиты второго основного энергетического состояния, W1.4 – W2.4 и W1.4 – W2.5. С пятой орбиты первого основного энергетического состояния (обозначена треугольником) возможен переход только на пятую орбиту второго основного энергетического состояния, W1.5 – W2.5. С шестой (обозначена двойным кружком) и с седьмой (обозначена крестом) орбит первого основного энергетического состояния возможны переходы только на шестую – седьмую (W1.6 – W2.6 и W1.6 – W2.7) и седьмую – восьмую (W1.7 – W2.7 и W1.7 – W2.8) орбиты второго основного энергетического состояния, соответственно.
Итак, не обращая внимания на заклинания современных шаманов, подчинивших себе физику экспериментальную и погрузивших мир теоретической физики в пучину средневековой религиозной тьмы, можно на основе доступной пониманию классической физики построить теоретическую модель простейшего атома, − атома водорода, наиболее полно соответствующую физической реальности.И нет в этой модели ни «магнетонов Бора», ни «постоянной Планка», ни «постоянной Ридберга», ни «спинов» Гаудсмита и Уленбека, ни «соотношения неопределенностей» Гейзенберга, ни «волновых свойств вещества» де Бройля, ни гипотетических «фотонов» Эйнштейна и т.п.
Все, что оказалось необходимым, − это законы сохранения энергии, импульса и момента импульса, законы классической механики и классической электродинамики, экспериментальное значение энергии ионизации. Ну и, разумеется, атомные спектры, которые необходимы не только для проверки правильности модели, но и для ее корректировки из-за недостаточной точности экспериментального определения энергии ионизации.
Это далеко не все, что можно рассказать об атоме водорода и его энергетическом строении. С более полной информацией о строении атома водорода (и не только водорода) можно ознакомиться в книге
