Первая спектральная серия атома водорода

5.1. Между энергетическим состоянием W₁ электрона на первой орбите радиуса R₁ и до отрыва электрона от атома могут существовать еще множество энергетических состояний (или энергетических уровней) с другими радиусами орбит и, но с моментом импульса, равным моменту импульса электрона на первой орбите. Причем эти уровни энергии соответствуют отрицательной энергии электрона, то есть соответствуют связанному состоянию электрона с ядром.

Согласно закону сохранения момента импульса, на всех орбитах электрона в первом основном энергетическом состоянии с порядковым номером орбиты n=2, 3, … электрон должен иметь тот же самый орбитальный момент импульса, что и на первой орбите:

,

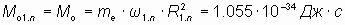(9)

где n – порядковый номер орбиты.

Выразим разность между угловой скоростью на первой орбите и угловой скоростью электрона на орбите с номером n через орбитальный момент импульса электрона, который для всех радиусов орбит первого основного энергетического состояния равен M_о/2.

,

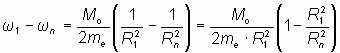или

.

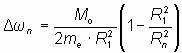(10)

Почему в формуле (10) следует брать только половину орбитального момента импульса? Изменение энергии атома или иона осуществляется посредством поглощения или излучения электромагнитных волн. Но электромагнитная волна не несет механический момент импульса, через который выражена разность угловых скоростей или угловых частот орбитального вращения электрона [4]. Поэтому при применении понятия механического момента к электромагнитной волне необходимо пользоваться энергетическими характеристиками. Это возможно потому, что энергия вращательного движения пропорциональна моменту импульса. Если перейти к энергетической характеристике момента импульса, то и электромагнитную волну следует рассматривать с тех же энергетических позиций. Поскольку элементарная электромагнитная волна состоит из двух одновременных электромагнитных колебаний электрического и магнитного полей, взаимно преобразующихся друг в друга [4], то каждое составляющее электромагнитное колебание несет половину энергии всей электромагнитной волны и, соответственно, эта энергия пропорциональна произведению половины орбитального момента импульса электрона на разность частот. То есть когда речь идет о разности энергий электрона в атоме, то его орбитальный момент импульса в основном состоянии равен M_о, а энергия − 0.5M_о∙Δω, но когда речь идет о длине волны или частоте электромагнитной волны, которые определяются в каждом из двух одновременных колебаний электромагнитного поля, то при выражении длины волны или частоты через момент импульса электрона необходимо использовать только половину величины момента M_о, а эквивалентная энергия этой половины электромагнитной волны − 0.25M_о∙Δω. Связь же величин в электромагнитной волне (λ=2π· с/ω ) одинакова в любом из двух составляющих волну электромагнитных колебаний.

Именно поэтому в соответствии с определением момента импульса и структурой элементарной электромагнитной волны [4] в формулу (10) входит половина орбитального момента импульса электрона.

Преобразуем разность частот (10) в соответствующую этой разности частот величину обратной длины волны:

.

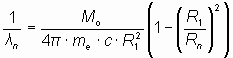(11)

В уравнении (11) величина, стоящая в правой части перед скобками, равна:

.

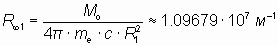(12)

Эта величина в формуле (12) соответствует так называемой «постоянной Ридберга», R_∞, которая в современной физике выражается через несколько другое соотношение некоторых других известных констант [2, 6]:

.

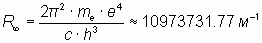Рассмотрим возможную длину электромагнитных волн соответствующих изменению энергетических уровней электрона в пределах основного энергетического состояния W₁.

Для того чтобы не изменился момент импульса электрона, допустимые длины волн излучаемого или поглощаемого электромагнитного излучения должны быть кратны длине окружности первой орбиты, то есть, кратны целому числу радиусов первой орбиты электрона:

.

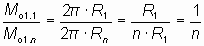(13)

Подставляя отношение (13) в формулу (12) получаем формулу для определения всех длин волн электромагнитного излучения (или поглощения) в первом основном энергетическом состоянии атома водорода в зависимости от номера орбиты электрона:

,

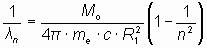(14)

где n=2, 3, … – это номера орбит и соответствующих им спектральных линий в первой основной серии атома водорода, называемой серией Лаймона.

5.2. Излучение и поглощение атомом электромагнитных волн с изменением энергетических уровней в пределах одного основного энергетического состояния является дипольным электрическим излучением [4].