Две задачи математического анализа

Основные правила дифференцирования

1. .

2. независимая переменная.

3. , где .

4. , .

5. ,

.

6. .

7. Производная сложной функции. Если , где .

8. Дифференциал функции. Если .

Таблица производных

1. Производная степенной функции

. Частные случаи : .

2. Производная показательной функции ,

; , так как ; , так как .

3. Производная логарифмической функции

; , так как ; , так как .

4. Производные тригонометрических функций

; ; ;

; ;

.

5. Производные обратных тригонометрических функций:

, ,

, .

6. Производные гиперболических функций:

, ,

, .

Неопределенный интеграл

Теорема существования. Если функция непрерывна в заданном промежутке , то в этом промежутке она имеет первообразную.

Основные свойства неопределенного интеграла

1. . 2. .

3. . 4. .

5. .

6. Если , то .

7. Если , то .

8. Если , то .

Методы интегрирования

1. Метод замены переменной (способ подстановки)

.

2. Метод интегрирования по частям: .

Таблица неопределенных интегралов

1. Интеграл от степенной функции :

; (1) . (2)

. (3)

2. .

3. Интеграл от показательной функции :

.

4. Интегралы от тригонометрических функций:

; ;

; ; ; ;

; .

5. Интегралы от гиперболических функций:

; ;

; .

6. Интегралы, содержащие выражение вида :

. (5) . (6)

. (7) . (8)

. (9) . (10)

7. Часто встречающиеся интегралы:

.

.

. (11)

. (12)

. (13)

. (14)

8. Реккурентные соотношения

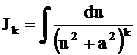; . (15)

; .

; .

Замечание

1. Во всех формулах подынтегральные функции предполагаются сложными,

т. е. аргумент и есть некоторая функция от независимой переменной х: . Следует хорошо уяснить, что все формулы верны лишь в том случае, когда подынтегральная функция умножается строго на дифференциал аргумента u, т. е. на . Так, например, , но , так как здесь , чего нет под интегралом. Аналогично , но , так как здесь , чего нет под интегралом.

Для упрощения записи во всех формулах независимая переменная х опущена. Например, формула (1) имеет следующий вид: . Такая запись затрудняет запоминание формулы.

2. Вся таблица интегралов разбита на восемь групп формул. Деление это, вообще говоря, произвольное, сделано с единственной целью, чтобы можно было быстрее и легче запомнить эти формулы. Впрочем, в большинстве случаев достаточно знать первые шесть групп формул. Седьмая группа выделена потому, что эти интегралы находятся достаточно длинным способом и встречаются на практике редко.

3. Следует научиться работать с рекуррентными соотношениями. Сущность их состоит в том, что, зная интеграл 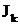, можно без труда найти интеграл

Приведем пример использования формулы (15). Полагая здесь 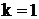, получим

(табличный интеграл (5)),

, .

При имеем ,

,

.

В заключение отметим, что существуют три способа отыскания неопределенных интегралов: интегрирование с помощью табличных формул (он называется иначе «метод подведения под знак дифференциала»), метод замены переменной (иначе: «способ подстановки») и метод интегрирования по частям. Подробно рассмотрим эти методы.

Упражнения (устно)

Дайте ответы в следующих примерах.

.

Упражнение

Найти следующие интегралы.

Задание на дом

Примеры.

.

Последний интеграл степенной, так как , если

, поэтому

.

.

Первый интеграл степенной: , где . Второй интеграл также степенной, его можно найти в примере . Поэтому

.

Упражнение. Решить примеры.

Упражнение

Найти интегралы

, .

Примеры

Многочлен 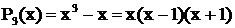имеет простые вещественные корни

.

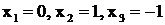Решение. Многочлен 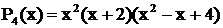имеет вещественный простой корень 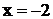; двукратный корень .

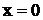Определение. Следующие рациональные дроби называются простейшими первого, второго, третьего и четвертого типов: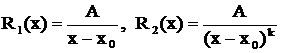

.

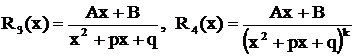Здесь 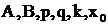- заданные числа, .

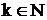В последующем постоянно предполагается, что трехчлен 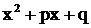не имеет

вещественных корней и, следовательно, не разлагается на линейные множители.

Примеры. Рассмотрим дроби

.

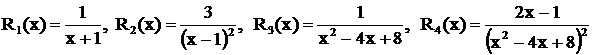Здесь 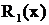- дробь первого типа, причем 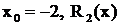- дробь второго типа, где 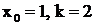. 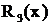- дробь третьего типа, где 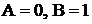, причем трехчлен 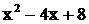вещественных корней не имеет. Дробь 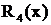принадлежит к четвертому типом, где .

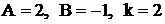Дроб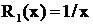и и 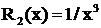принадлежат соответственно к первому и второму типам, причем .

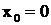Теорема о разложении рациональной дроби. Всякая правильная рациональная дробь разлагается в сумму простейших дробей первого – четвертого типов. При этом если 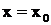- простойвещественный корень знаменателя 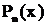, то в разложении ему соответствует дробь первого типа 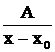; если 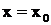- вещественный корень кратностью k, то в разложении ему соответствует сумма k дробей первого и второго типов:

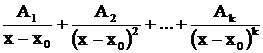; если в знаменателе 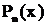имеется трехчлен 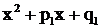без вещественных корней, то в разложении дроби ему соответствует дробь третьего типа 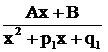; если, наконец, знаменатель 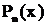содержит множитель 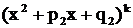, то в разложении ему соответствует сумма «k» дробей третьего и четвертого типов: .

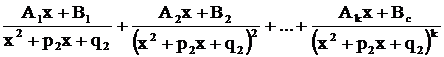Таким образом, разложение дроби 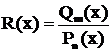существенно зависит от того, какие корни имеет знаменатель 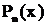. Поэтому разложение рекомендуется проводить по следующей схеме.

1. Найти все корни знаменателя 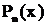и определить их кратность.

2. Написать разложение 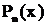на линейные и квадратные множители.

3. Написать сумму простейших дробей в соответствии с полученным разложе-нием знаменателя.

Пример 1. Разложить дробь .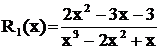

Решение. Здесь знаменатель имеет разложение 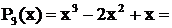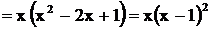. Отсюда следует, что 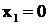- простой вещественный корень, ему соответствует дробь 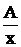; 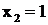- вещественный двукратный корень, ему соответствует сумма дробей 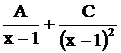. Поэтому данная дробь представлена суммой .

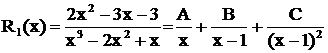Пример 2. Разложить дробь .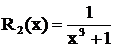

Решение. Здесь 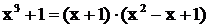, причем трехчлен вещественных корней не имеет, поэтому .

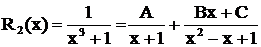Пример 3.Разложить дробь .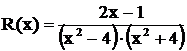

Решение. Здесь знаменатель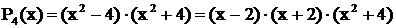

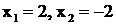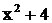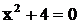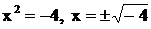имеет вещественные простые корни: . Двучлен веществен-ных корней не имеет: если , то . Поэтому разло-жение дроби имеет вид

.

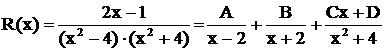Теперь перейдем к нахождению неопределенных коэффициентов разложения: А, В, С,…. Существуют два способа их определения. Поскольку оба способа достаточно простые, рассмотрим их на конкретных примерах.

Первый способ. Дробь 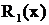представлена в виде

.

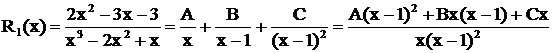Поскольку здесь знаменатели равны, то должны быть равны и числители.

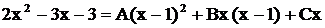. Имеет место равенство двух многочленов, которое выполняется тождественно, т.е. при любых значениям «х».

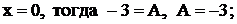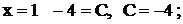Пусть, например, при при 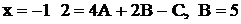. Таким образом, получили разложение дроби .

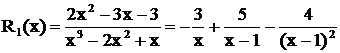Замечание. Нахождение неопределенных коэффициентов А, В, С, … упрощается, если в качестве значений «х» брать корни знаменателя.

Второй способ покажем на следующем примере:

,

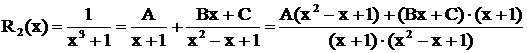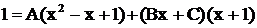. В правой части раскроем скобки и приведем подобные члены, тогда 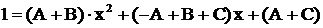или 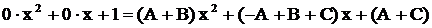. Приравнивая коэффициенты при одинаковых степенях х и свободные члены, получаем систему линейных уравнений относительно А, В, С: 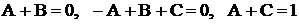. Решив эту систему способом подстановки (или по формулам Крамера), получим 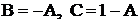. Подставим эти значения во второе равенство: 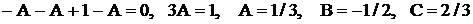. Получаем разложение дроби .

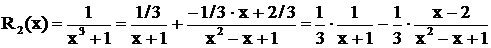Замечание. Результат вычислений всегда можно проверить. Так, в последнем примере .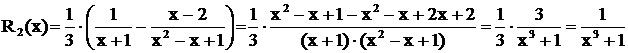

Упражнение. Разложить на простейшие дробь 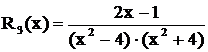. Разложив дробь 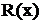на простейшие и проинтегрировав полученное равенство, получим в правой части (в общем случае) сумму следующих четырех интегралов:

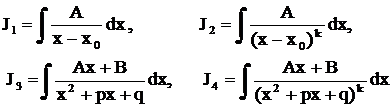
Первый из них по существу табличный: 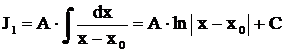. Второй интеграл степенной:

.

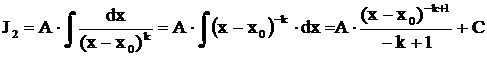Третий интеграл был рассмотрен выше.

Рассмотрим подробнее интеграл 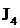, 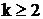. Так как 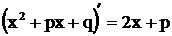, чи-слитель представляем в виде 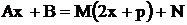, 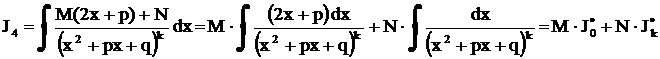. Интеграл 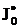степенной, так как

.

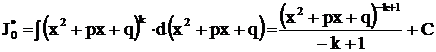Для нахождения интеграла 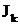выделим из трехчлена полный квадрат:

.

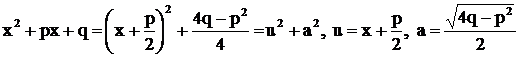Тогда 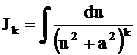. Этот интеграл находится с помощью рекуррентного соотношения (15). Впрочем интеграл может быть найдем с помощью тригонометрической подстановки .

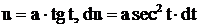Пример. Найти интеграл .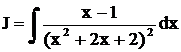

Решение.Так как 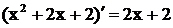, получим .

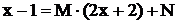Тогда .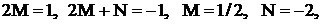

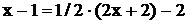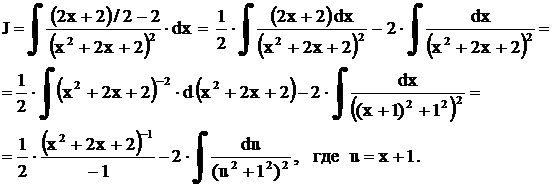
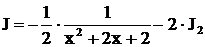. Полагая в формуле (15) 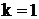, получим

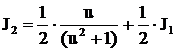, где ,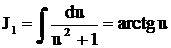

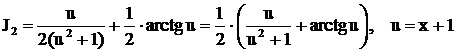. Окончательно находим

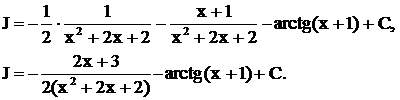
Для сравнения найдем 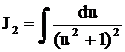, где 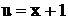с помощью подстановки 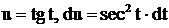. Тогда 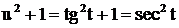. Поэтому

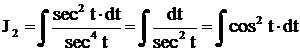. Так как 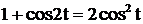, получим

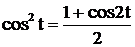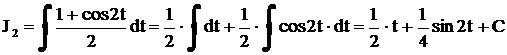, . Из подстановки следует, что ,

,

.

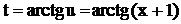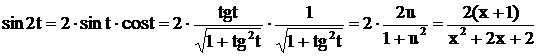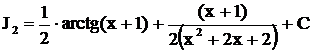Решить примеры

.

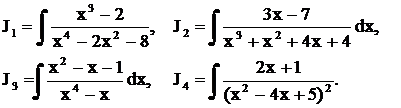Решение.

,

,

.

Интегралы вида , , где m – целое положительное число, находятся с помощью тождеств , .

Пример.

Пример. Найти интеграл .

Решение.

.

Следующие три интеграла берутся с помощью известных формул тригонометрии ,

,

.

Пример. Найти интеграл .

Решение.

, .

Подстановка рекомендуется для нахождения интеграла , а

также в тех случаях, когда в интеграле числа m и n - четные (положительные или отрицательные). Здесь используются известные формулы тригонометрии: .

Пример.Найти интеграл .

Решение. ,

,

. Так как , то окончательно

получим .

Замечание. Для интегралов где k- натуральное число, методом интегрирования по частям можно получать рекуррентные соотношения, приведенные в таблице интегралов.

Решить самостоятельно

, .

Выше были рассмотрены основные приемы и формулы для нахождения неопределенных интегралов. Следует отметить, что многие функции не интегрируются в конечном виде. Так, например, функция непрерывна в промежутке , однако, интеграл от нее (интегральный синус) не выражается в конечном виде через элементарные функции. То же самое относится к

интегралам (интегральный косинус), (интегральный

логарифм).

Замечание. Во многих случаях заданный интеграл может быть найден различными способами. Так, например, интеграл с помощью подстановки дает , где , . С другой стороны, если возьмем подстановку , то .

Поэтому .

Окончательно . Этот результат лишь формой отличается от предыдущего, так как

.

Две задачи математического анализа

Первая задача состоит в отыскании производной от заданной функции . Напомним, что с помощью производной решаются многие задачи математики и физики. Так, например, если точка движется по закону , где t – время, а S – пройденный путь, то скорость движения есть производная от пути по времени, т. е. , а ускорение равно . Если масса неоднородного стержня изменяется по закону , то его плотность в точке х есть производная . В геометрии с помощью производной решается задача о проведении касательных к заданным кривым. Эти примеры можно продолжить.

Теперь обратимся к обратной задаче: как по заданной производной восстановить саму функцию ?

Как, например, зная скорость движения , найти закон изменения пройденного пути ? Как найти массу стержня переменной плотности ? В общем случае задача ставится следующим образом: пусть задана функция , производная от которой совпадает с заданной функцией: . Такая функция называется первообразнойфункции . Так, например, если , то , так как . Если , то , так как . Обратите внимание на то, что для заданной функции первообразных существует бесконечно много, так как есть некоторая первообразная . Любая функция вида , где , есть также первообразная , так как .

В силу этого множество всех первообразныхзаданной функции принято обозначать символом и называть неопределенным интегралом от функции . Итак, по определению, .

Примеры. , так как .

, так как .

, так как .

Приступая к изучению неопределенного интеграла, следует обратить внимание на то, что

1) эта операция многозначная;

2) в техническом отношении интегрирование для студентов представляется более сложным, чем отыскание производных. Чтобы научиться интегрировать, нужна практика. Только решение большого числа разнообразных примеров позволит выработать некоторые навыки в интегрировании;

3) обратите внимание на запись интеграла. Здесь под знаком интеграла стоит дифференциал аргумента функции . Если же задана сложная функция , где , то все формулы интегрирования имеют смысл только в том случае, когда под знаком интеграла стоит дифференциал . Это обстоятельство нужно иметь в виду постоянно. В формуле будем подразумевать, что ищется интеграл от сложной функции , где , х – независимая переменная;

4) существуют шесть тригонометрических функций:

. Последние две функции определяются как величины, обратные по отношению к , т. е. .

Это позволяет известные формулы тригонометрии

записывать в целом виде:

.

Таблицы производных и интегралов поэтому имеют более простой вид. При интегрировании гиперболических функций , , , следует помнить основные формулы, связывающие их: , а также формулы понижения ;

5) поскольку операции дифференцирования и интегрирования тесно связаны, ниже приводятся основные свойства производной и формулы дифференцирования, а далее – аналогичный материал, касающийся неопределенного интеграла.