Относительные атомные массы исследуемых изотопов

12C 13C 14C

12,0000 13,0034 14,0032

20Ne 21Ne 22Ne

19,9924 20,9939 21,9914

234U 235U 238U

234,0409 235,0439 238,0508

Вопросы и задания для самоконтроля.

1. Как определяется направление действия силы Лоренца?

2. Почему сила Лоренца не совершает работы?

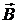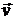3. Как будет двигаться заряженная частица в магнитном поле, если угол a между векторами и меньше p/2?

4. Ионы двух изотопов с массами m₁ и m₂ , имеющие одинаковый заряд и прошедшие в электрическом поле одинаковую ускоряющую разность потенциалов, влетают в магнитное поле перпендикулярно силовым линиям магнитного поля. Найдите отношение радиусов окружностей, по которым будут двигаться ионы в магнитном поле.

5. Определите, во сколько раз изменится радиус окружности, по которой заряженная частица движется в однородном магнитном поле, если её кинетическую энергию увеличить в n раз?

6. Что представляет собой масс-спектрометр? Каков его принцип действия? Для чего он используется?

7. Определите удельный заряд иона, который в масс-спектрометре совершает один оборот за 628 мкс в однородном магнитном поле с индукцией 50 мТл.

8. Пучок ионов, влетающих в вакуумную камеру масс-спектрометра перпендикулярно силовым линиям однородного магнитного поля, расщепляется (рис.3). Определите, какая траектория соответствует: а) большему импульсу,

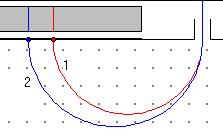
Рис.3

если ионы имеют одинаковые заряды, но разные импульсы; б) большему заряду, если частицы имеют одинаковые импульсы, но разные заряды?

9. Два электрона движутся в одном и том же однородном магнитном поле по орбитам с радиусами R₁ и R₂ (R₁> R₂). Сравните их угловые скорости.

10. В однородном магнитном поле движутся по окружностям протон и a-частица, имея равные кинетические энергии. Какая из этих частиц будет иметь период вращения больше и во сколько раз?

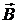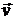11. Заряженная частица влетела в однородное магнитное поле под углом a < p/2 между векторами и . Определите, отличны ли от нуля тангенциальная и нормальная составляющие ускорения частицы?

12. Заряженная частица летит прямолинейно и равномерно в однородном электромагнитном поле, представленном суперпозицией взаимно перпендикулярных электрических (напряжённостью Е) и магнитных (индукцией В) полей. Найдите скорость движения частицы.

13. Рассчитайте значение относительной атомной массы неона, если относительное содержание его изотопов ²⁰Ne, ²¹Ne и ²²Ne составляет 90,51%, 0,27% и 9,22% соответственно.

14. Рассчитайте значение относительной атомной массы урана, если относительное содержание его изотопов ²³⁴U, ²³⁵U и ²³⁸U составляет 0,0055%, 0,7200% и 99,2745% соответственно.

15. Значение относительной атомной массы меди равно 63,55. Известно, что у этого элемента есть два изотопа с массовыми числами 63 и 65. Определить процентное содержание изотопов.

ЛАБОРАТОРНАЯ РАБОТА И ИРГЗ № 2.

СПЕКТР ИЗЛУЧЕНИЯ АТОМАРНОГО ВОДОРОДА

ЦЕЛЬ РАБОТЫ:

* Знакомство с планетарной и квантовой моделями атома при моделировании процесса поглощения и испускания электромагнитного излучения атомами водорода.

* Экспериментальное подтверждение закономерностей формирования линейчатого спектра излучения атомарного водорода при низких давлениях.

* Экспериментальное определение постоянной Ридберга.

Ознакомьтесь с теорией в учебниках: 1. Савельев, Физика, т.3, §12, §28. 2. Глинка, Общая химия, гл. 2, §2.2, 2.5..

Запустите программу «Открытая химия». Выберите модель 2.2.«Атом водорода». Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект.

КРАТКАЯ ТЕОРИЯ:

1. СПЕКТРОМ электромагнитного излучения (ЭМИ) называется совокупность электромагнитных волн, излучаемых или поглощаемых атомами (молекулами) данного вещества.

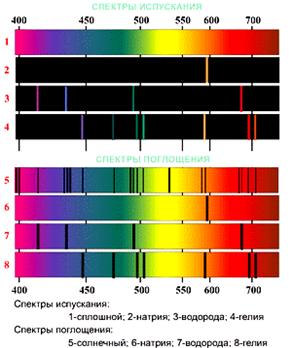
ЛИНЕЙЧАТЫЙ спектр состоит из отдельных компонент (линий), близких к гармоническим. Расстояние между линиями (по шкале длин волн или частот) много больше ширины линий. Такой спектр характерен для атомарных газов (см. рис. 1).

Еще в 1885 г. швейцарский физик и математик Иоганн Бальмер установил, что длины волн, соответствующие определенным линиям в спектре атомов водорода, можно выразить как ряд целых чисел. Предложенное им уравнение, позднее модифицированное шведским физиком Юханнесом Ридбергом, имеет вид:

Рис. 1. Спектры ЭМИ атомов.

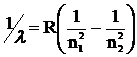, (1)

где λ – длина волны; R – постоянная Ридберга для атома водорода, n₁ и n₂ – целые числа, причем n₁ < n₂.

Кроме линейчатого выделяют еще ПОЛОСАТЫЙ спектр, который излучают молекулярные газы, и СПЛОШНОЙ спектр, излучаемый нагретыми твердыми телами.

2. ПЛАНЕТАРНАЯ МОДЕЛЬ АТОМА: в центре атома расположено очень малое по размеру положительно заряженное ядро, вокруг которого по определенным (разрешенным) стационарным орбитам движутся электроны, масса которых во много раз меньше массы ядра. При движении по стационарной орбите электрон не испускает электромагнитного излучения (ЭМИ). При поглощении ЭМИ (фотона) электрон переходит на более «высокую по энергии» разрешенную орбиту, на которой его энергия становится больше на величину DЕ_ЭЛ, равную энергии поглощенного фотона Е_Ф. При обратном переходе электрон испускает фотон с такой же энергии: Е_Ф = |DЕ_ЭЛ|. Энергия фотона связана с частотой ЭМИ по формуле Планка:

E_Ф = h·ν = h·c / λ, (2)

где ν – частота, с^-1; h – постоянная Планка; с – скорость света, м/с, λ – длина волны, м.

КВАНТОВАЯ модель атома отличается от планетарной в первую очередь тем, что в ней электрон не имеет точно определенной координаты и скорости, поэтому бессмысленно говорить о траектории его движения. Можно определить (и нарисовать) только границы области его преимущественного движения (орбитали).

УРАВНЕНИЕ ШРЕДИНГЕРА для движения электрона в кулоновском поле ядра атома водорода используется для анализа квантовой модели атома. В результате решения этого уравнения получается волновая функция, квадрат модуля которой и определяет плотность вероятности нахождения электрона в данной области пространства. Волновая функция зависит не только от координаты 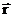и времени t, но и от 4-х параметров, имеющих дискретный набор значений и называемых квантовыми числами.

Главное КВАНТОВОЕ ЧИСЛО n может принимать положительные целочисленные значения 1, 2, 3... . Оно определяет величину энергии электрона в атоме. Состояния электрона с одинаковой энергией называются вырожденными. Кратность вырождения равна количеству состояний с одной и той же энергией.

ОРБИТАЛЬНОЕ (АЗИМУТАЛЬНОЕ) КВАНТОВОЕ ЧИСЛО l определяет модуль момента импульса электрона при его орбитальном движении 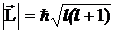и принимает целочисленные значения l = 0, 1, 2, ... n-1 . Оно определяет форму атомной орбитали.

МАГНИТНОЕ КВАНТОВОЕ ЧИСЛО m_l определяет проекцию вектора момента импульса орбитального движения электрона L_Z на направление внешнего магнитного поля 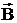. Оно принимает положительные и отрицательные целочисленные значения, по модулю меньшие или равные l . 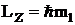, где m_l = 0, ±1, ±2, ... , ±l . Значение квантового числа m_l определяет расположение орбитали в пространстве.

МАГНИТНОЕ СПИНОВОЕ КВАНТОВОЕ ЧИСЛО m_Sопределяет проекцию вектора собственного момента импульса электрона (СПИНА 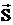) на направление внешнего магнитного поля 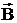: S_Z = 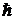m_S и принимает только 2 значения: m_S = +1/2, -1/2. Для модуля спина 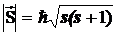, где s – спиновое квантовое число, которое у каждой частицы имеет только одно значение. Например, для электрона s = 1/2 (аналогично, для протона и нейтрона), для фотона s = 1.

КРАТКАЯ запись состояния электрона в атоме (электронная конфигурация): ЦИФРОЙ указывают значение главного квантового числа, буквОЙ – значение азимутального квантового числа, ВЕРХНИМ ИНДЕКСОМ – количество электронов на данной орбитали:

Буква	s	p	d	f	g
Значение l

ПРАВИЛО ОТБОРА орбитального квантового числа Dl = ±1. Электрон в атоме может переходить только между состояниями, удовлетворяющими указанному правилу.

СПЕКТРАЛЬНОЙ СЕРИЕЙ называется совокупность линий излучения, соответствующих переходу электрона в атоме на один и тот же нижний уровень энергии (серии в атоме водорода называются по именам их первооткрывателей):

Серия	Лаймана	Бальмера	Пашена	Брэкета
Переходы	np®1s	ns®2p, nd®2p	nf®3d, np®3d	ng®4f, nd®4f

На рис. 2 изображены некоторые из возможных переходов, разрешенных по правилам отбора, в атоме водорода.

Серия Лаймана   Серия Бальмера   Серия Пашена

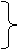
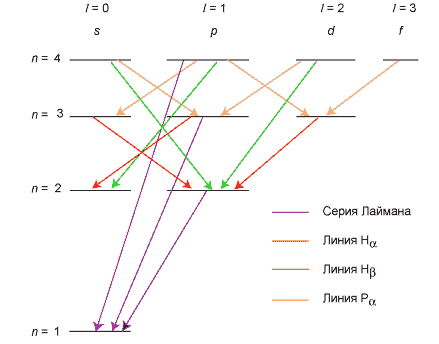
Рис. 2. Разрешенные переходы в атоме водорода.

3. МОДЕЛЬ АТОМА ВОДОРОДА ПО БОРУ. При движении электрона по разрешенной круговой орбите момент количества движения электрона (mvr) принимает определенные дискретные значения, а именно:

mvr = nh / 2π , (3)

где m – масса электрона, v – его скорость, r – радиус орбиты, h – постоянная Планка, n – главное квантовое число. Условие устойчивости такой орбиты – равенство центробежной силы и силы кулоновского притяжения:

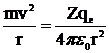, (4)

где q_e – заряд электрона, Z – заряд ядра, ε₀ – диэлектрическая проницаемость вакуума. Из этих условий Бор определил значения радиусов разрешенных орбит и энергию электрона на этих орбитах в атоме водорода:

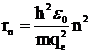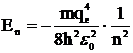, , (5)

Знак минус обозначает, что при образовании атома водорода из протона и электрона энергия выделяется. Если подставить численные значения всех постоянных в эти формулы, получится:

r_n = 0,529·10^-10·n² (м); E_n = – 13,6 / n² (эВ) = – 2,18·10^-18 / n², (Дж). (6)

На рис. 3. изображена компьютерная модель атома водорода с 6 стационарными орбитами.

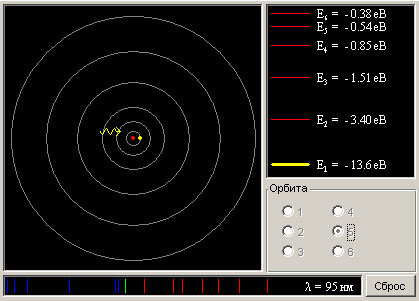
Рис. 3.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

Подведите маркер мыши к номеру орбиты электрона, указанному в таблице 1 для вашего варианта, и нажмите левую кнопку мыши.

ТАБЛИЦА 1. (не перерисовывать)