Операторы координаты и импульса

,

.

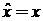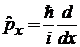Эрмитовый оператор

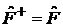. (2)

Операция эрмитового сопряжения «+» определяется в виде

,

.

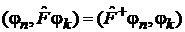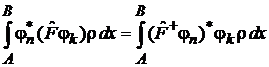Эрмитовый оператор в скалярном произведении функций можно переносить от одного сомножителя к другому

,

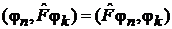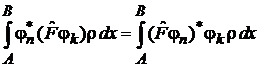. (3)

Любой физический оператор является эрмитовым, это обеспечивает вещественность его собственных значений, т. е. результатов измерения соответствующей физической величины.

Соотношения между матричными элементами

· Для эрмитового оператора

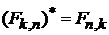(4)

– комплексное сопряжение обращает направление перехода между состояниями, т. е. течение времени: .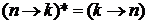

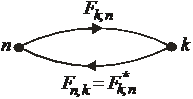
Доказательство:

С учетом

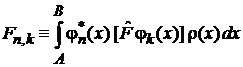, (1)

получаем

.

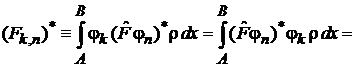
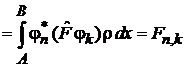Третье равенство следует из эрмитовости (3) оператора.

· Матричный элемент произведения эрмитовых операторов

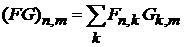(5)

– переход 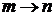под действия операторов 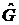и 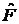происходит через все возможные промежуточные состояния k.

Доказательство:

Из определения матричного элемента (1) и эрмитовости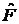

.

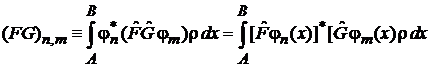Используем фильтрующее свойство δ-функции

,

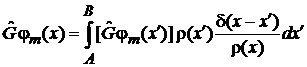тогда

.

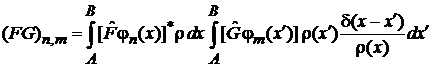Условие полноты базиса

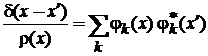
после замены порядка суммирования и интегрирований дает

.

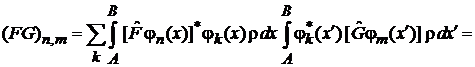
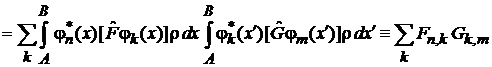ПРИМЕРЫ

1. Для матричного элемента оператора координаты гармонического осциллятора доказать

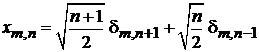, (П.4.6)

где 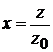– безразмерная, .

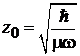Для оператора 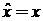по определению

.

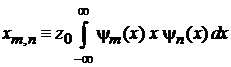Устраняем множитель x под интегралом рекуррентным соотношением

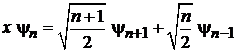, (6.34)

тогда

.

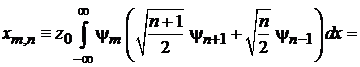
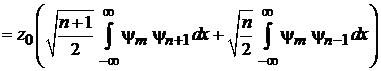Вычисляем интегралы при помощи условия ортонормированности

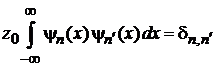. (6.33)

Получаем

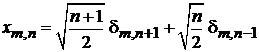, (П.4.6)

В частности

,

,

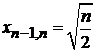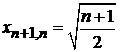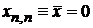. (П.4.7)

Матричные элементы вещественные, тогда из

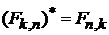(4)

получаем

.

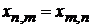2. Для оператора импульса 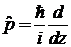найти матричный элемент

,

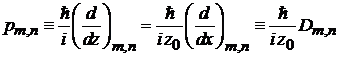где

;

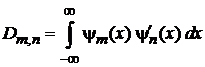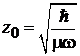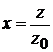; – безразмерная.

В 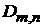устраняем производную под интегралом, используя рекуррентное соотношение:

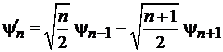. (6.39)

Получаем

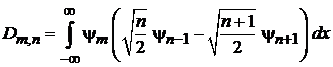
Вычисляем интегралы при помощи условия ортонормированности

,

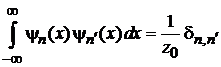находим

.

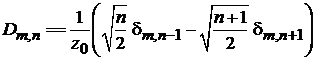Частные результаты:

,

,

.

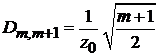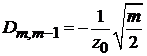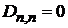Матричные элементы импульса:

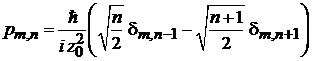, (П.4.11)

, ,

, ,

,

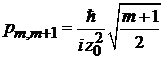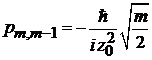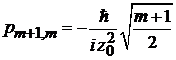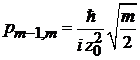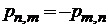среднее значение

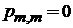. (П.4.12)

3. Доказать, что фурье-преобразование не изменяет форму уравнения гармонического осциллятора.

Фурье-преобразование уравнения

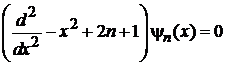(6.31)

с учетом

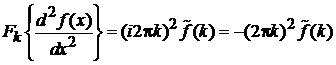, (1.35)

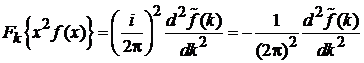(1.37)

дает

.

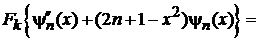
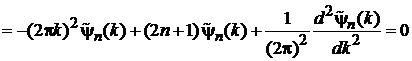Заменяем 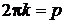, получаем

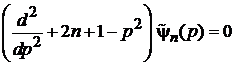, (П.4.14)

где 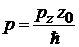– безразмерный импульс;

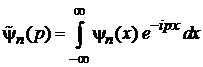. (П.4.15)

4. Для полиномов Эрмита доказать формулу Мелера

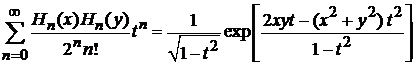, (П.4.20)

где 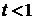. Получить формулу при .

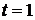Используем интегральное представление полиномов Эрмита

,

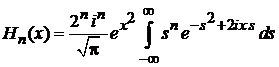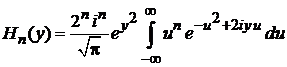. (6.8)

Меняем порядок суммирования и интегрирований

.

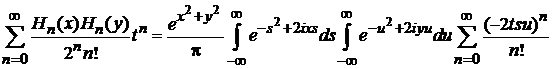Учитываем

,

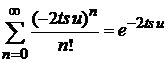тогда

.

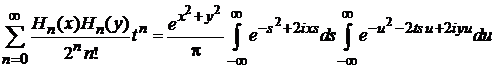Используем

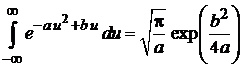(П.2.5)

при

, , ,

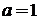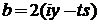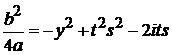и вычисляем внутренний интеграл

,

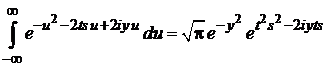тогда

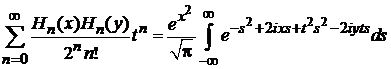. (П.4.20а)

Последний интеграл находим при помощи (П.2.5)

, ,

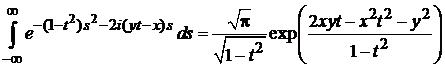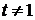и получаем (П.4.20).

При 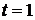последний интеграл дает дельта-функцию

,

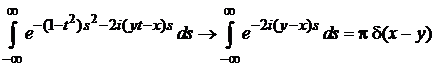где учено

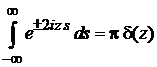. (2.24)

Из (П.4.20а) получаем условие полноты базиса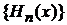

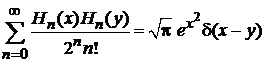. (П.4.21)

Для базиса функций гармонического осциллятора 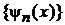, где

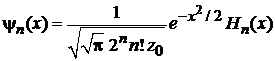, (6.32)

получаем условие полноты

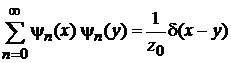. (П.4.22)

Обобщенные полиномы Лагерра

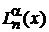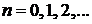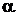, ; – любое число; .

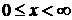Набор полиномов образует ортонормированный базис на полуоси .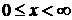

Используются:

· в теории измерительной техники и в теории систем связи;

· в квантовой механике описывают радиальное движение электрона в атоме.

Полиномы 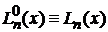исследовал Эдмон Никола Лагерр в 1878 г.

Обобщенные полиномы 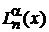изучал Николай Яковлевич Сонин в 1880 г., поэтому их называют также полиномами Сонина–Лагерра.

Уравнение Лагерра

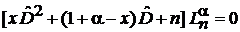(6.41)

является гипергеометрическим уравнением.

Формула Родрига

Методом факторизации ранее получена весовая функция

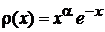. (П.3.9)

Из (П.3.10) при

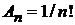
находим

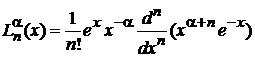. (6.42)