Классические ортогональные полиномы

КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ

Полином (многочлен) порядка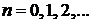

.

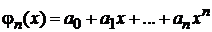Условие ортогональности

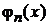– орт,

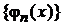– базис в гильбертовом пространстве сусловием ортонормированности

,

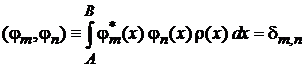где

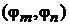– скалярное произведение функций;

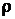– весовая функция;

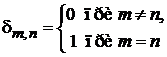– символ Кронекера.

Классические ортогональные полиномы некоторого типа являются частными решениями дифференциального уравнения обобщенного гипергеометрического типа – полиномы Эрмита, Лагерра, Лежандра, Чебышева, Якоби, Гегенбауэра.

Полиномы Эрмита

, ; .

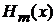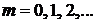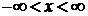Применяются в оптике, в математической статистике, в теории вероятностей, в квантовой механике.

Полиномы исследовали Пафнутий Львович Чебышев в 1859 г. и Шарль Эрмит в 1864 г., они называются также полиномами Чебышева–Эрмита.

Уравнение Эрмита

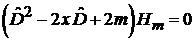. (6.1)

Формула Родрига

Методом факторизации ранее получено решение (П.3.3). Доопределяем 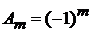, тогда

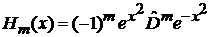. (6.2)

Весовая функция (П.3.1)

.

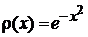Из (6.2)

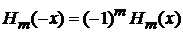. (6.3)

Полиномы низших степеней

Из (6.2) с учетом

, , , …

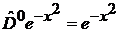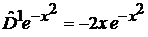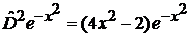находим

, ,

, ,

, .

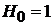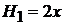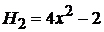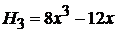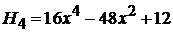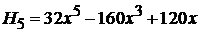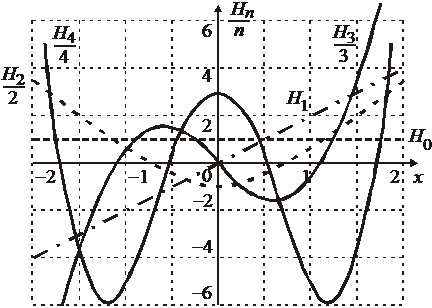
Полиномиальная форма

Обобщаем частные результаты

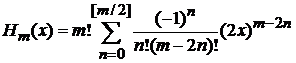, (6.4)

где 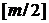– целая часть .

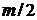Интегральное представление

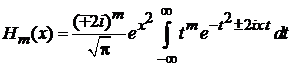(6.8)

применимо как для целых положительных m, так и для дробных и для отрицательных m.

Доказательство (6.8):

Теорема Фурье о дифференцировании

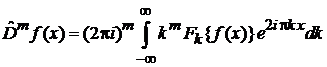Для 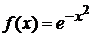учитываем (П.2.6)

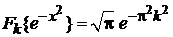тогда

.

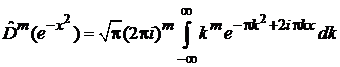Под интегралом заменяем :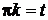

,

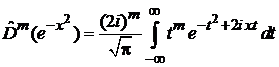Подстановка в (6.2)

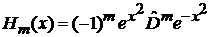дает

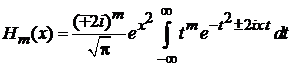, (6.8)

где комплексное сопряжение не меняет вещественный полином.

Производящая функция

Методом факторизации ранее получено (П.3.5)

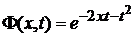. (6.10)

Из (5.14)

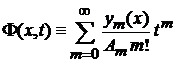с 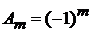получаем

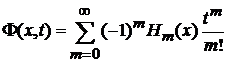. (6.11)

Рекуррентные соотношения для полиномов

Алгоритм получения:

1. Дифференцируем (6.10) по одному из аргументов.

2. В полученное соотношение подставляем (6.11).

3. Приравниваем слагаемые с одинаковыми степенями t.

Соотношение 1 для полинома Эрмита

Из

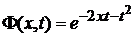(6.10)

получаем

.

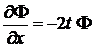Подставляем (6.11)

,

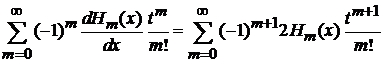приравниваем слагаемые с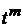

,

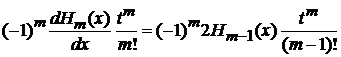получаем

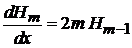, (6.12)

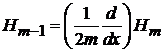. (6.13)

Соотношение 2

Из

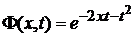(6.10)

получаем

.

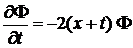Подставляем

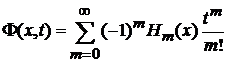, (6.11)

находим

,

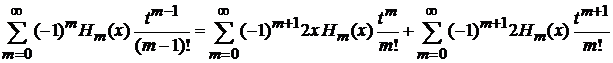приравниваем слагаемые с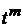

,

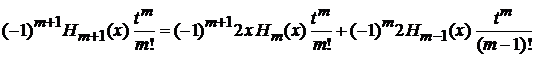Получаем

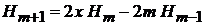. (6.15)

Учет

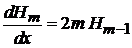(6.12)

дает

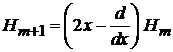. (6.16)

Условие ортонормированности

Множество 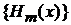образует базис в гильбертовом пространстве функций, определенных при , сусловием ортонормированности (П.3.4)

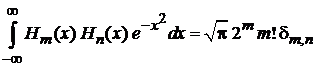. (6.18)

Разложение функции по полиномам Эрмита

Если 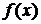определена при 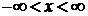, то она разлагается по базису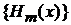

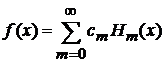. (6.19)

Находим коэффициент :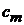

· умножаем (6.19) на ,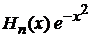

· интегрируем по интервалу ,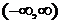

· меняем порядок суммирования и интегрирования,

· учитываем ортонормированность (6.18),

· символ Кронекера снимает сумму, оставляя одно слагаемое:

.

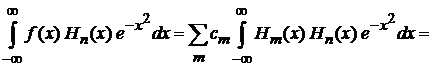
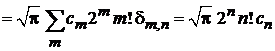Заменяем 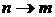и получаем

.

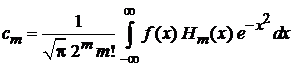· Подставляем полином в форме Родрига

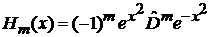, (6.2)

получаем

.

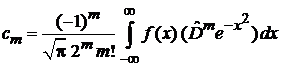Интегрируем по частям m раз, свободные слагаемые зануляются на обоих пределах, получаем коэффициент

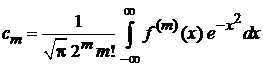. (6.20)

Гармонический осциллятор

Система, колеблющаяся по гармоническому закону. От лат. oscillatio – «качание».

Осциллятор в квантовой теории

В квантовой теории спектр энергии эквидистантный

, ,

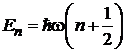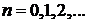уровню n сопоставляются n квантов энергии ;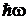

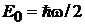– энергия вакуума.

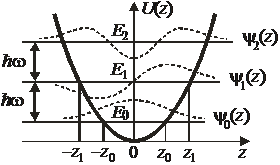
Уравнение Шредингера

.

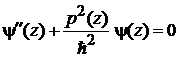Для осциллятора учитываем

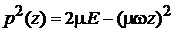, (6.30)

получаем для состояния уравнение

.

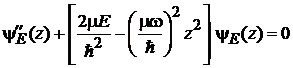Переходим к безразмерной координате

, ,

, ,

,

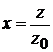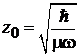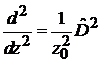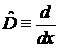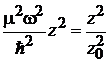Для

,

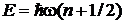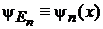
с учетом

,

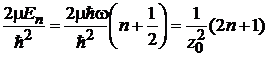получаем уравнение

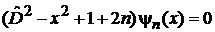, (6.31)

Методом факторизации ранее получено решение (П.3.6) в виде функции Эрмита

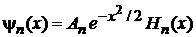. (6.32)

Из (6.3)

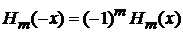и (6.32) находим

.

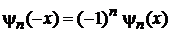Условие ортонормированности

Из (П.3.7)

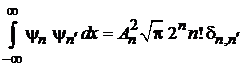при

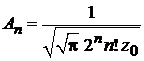
получаем

,

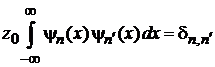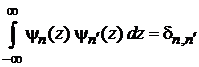. (6.33)

Учитывая 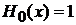, , 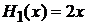, 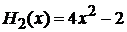из (6.32) находим основное состояние

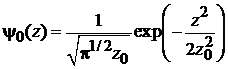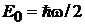, (6.33а)

и первое возбужденное состояние

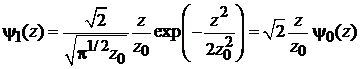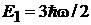, . (6.33б)

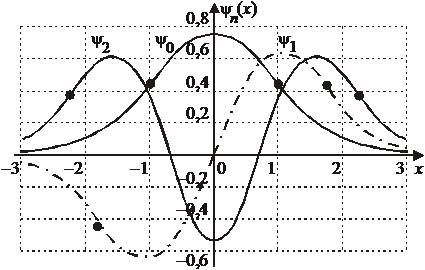
Точки поворота классического осциллятора

, , , .

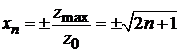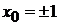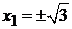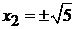Рекуррентные соотношения

· Умножаем (6.15)

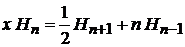на 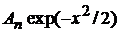и учитываем

, , ,

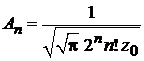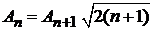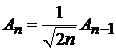для

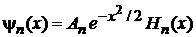. (6.32)

находим

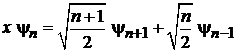. (6.34)

· Дифференцируем

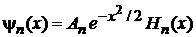, (6.32)

.

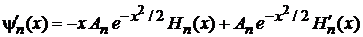Учитываем (6.12)

, ,

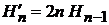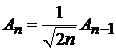Получаем

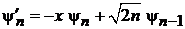. (6.35)

Из (6.35)

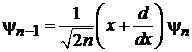. (6.36)

· Из

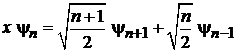(6.34)

выражаем

.

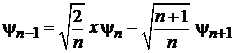Подстановка в (6.35) дает

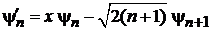. (6.37)

Из (6.37) находим

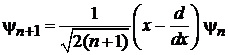. (6.38)

· Суммирование (6.35) и (6.37) дает

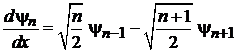. (6.39)

Лестничные операторы

Изменяют состояние n на единицу

,

.

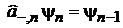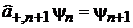Из (6.36) и (6.38) получаем

,

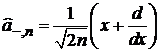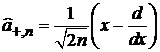. (6.40)

Матричный элемент

Вероятность перехода системы между состояниями 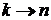под действие оператора 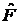выражается матричным элементом 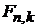. По индексам переход происходит справа налево.

Математический смысл

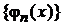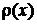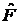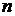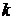В гильбертовом пространстве с базисом и весовой функцией матричный элемент оператора между ортами и определяется в виде скалярного произведения

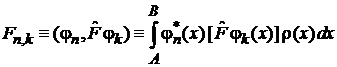, (1)

где A, B, 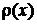– вещественные.

Физический смысл

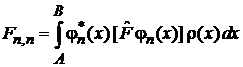
– диагональный матричный элемент есть среднее значение величины f, описываемой оператором 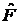, в состоянии .

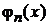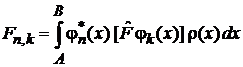
– недиагональный матричный элемент 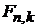есть амплитуда вероятности переходамежду состояниями 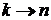под действием оператора .

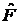Вероятность перехода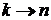

.

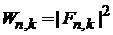Эрмитовый оператор

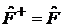. (2)

Операция эрмитового сопряжения «+» определяется в виде

,

.

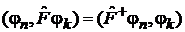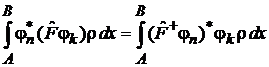ПРИМЕРЫ

1. Для матричного элемента оператора координаты гармонического осциллятора доказать

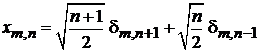, (П.4.6)

где 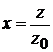– безразмерная, .

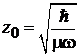Для оператора 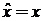по определению

.

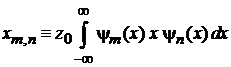Устраняем множитель x под интегралом рекуррентным соотношением

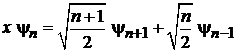, (6.34)

тогда

.

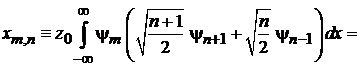
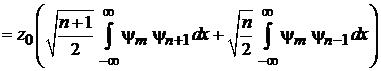Вычисляем интегралы при помощи условия ортонормированности

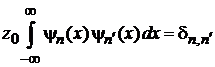. (6.33)

Получаем

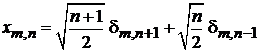, (П.4.6)

В частности

,

,

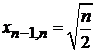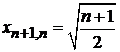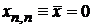. (П.4.7)

Матричные элементы вещественные, тогда из

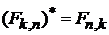(4)

получаем

.

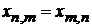2. Для оператора импульса 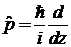найти матричный элемент

,

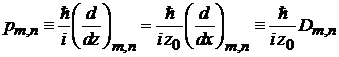где

;

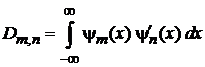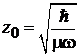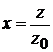; – безразмерная.

В 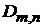устраняем производную под интегралом, используя рекуррентное соотношение:

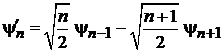. (6.39)

Получаем

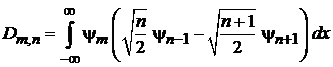
Вычисляем интегралы при помощи условия ортонормированности

,

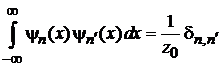находим

.

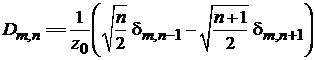Частные результаты:

,

,

.

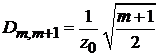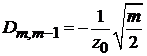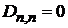Матричные элементы импульса:

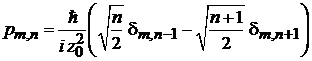, (П.4.11)

, ,

, ,

,

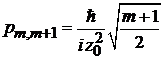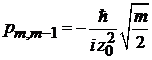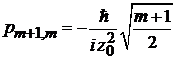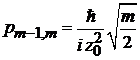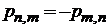среднее значение

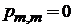. (П.4.12)

3. Доказать, что фурье-преобразование не изменяет форму уравнения гармонического осциллятора.

Фурье-преобразование уравнения

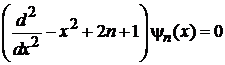(6.31)

с учетом

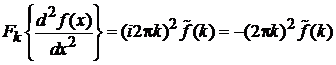, (1.35)

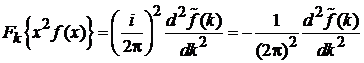(1.37)

дает

.

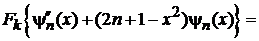
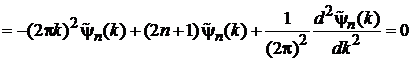Заменяем 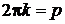, получаем

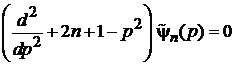, (П.4.14)

где 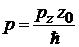– безразмерный импульс;

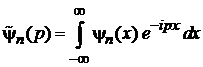. (П.4.15)

4. Для полиномов Эрмита доказать формулу Мелера

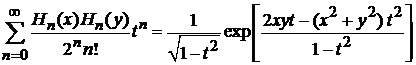, (П.4.20)

где 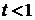. Получить формулу при .

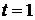Используем интегральное представление полиномов Эрмита

,

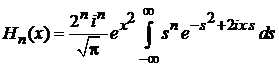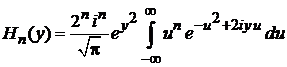. (6.8)

Меняем порядок суммирования и интегрирований

.

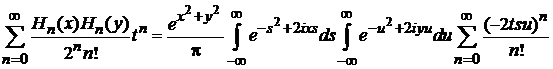Учитываем

,

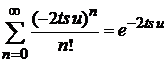тогда

.

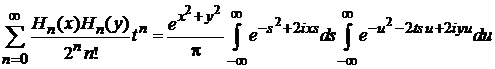Используем

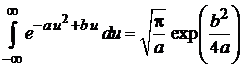(П.2.5)

при

, , ,

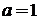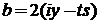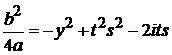и вычисляем внутренний интеграл

,

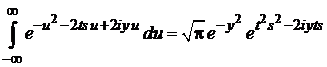тогда

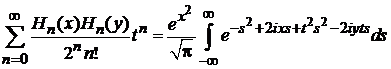. (П.4.20а)

Последний интеграл находим при помощи (П.2.5)

, ,

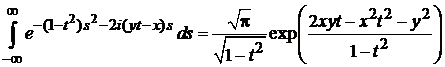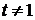и получаем (П.4.20).

При 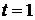последний интеграл дает дельта-функцию

,

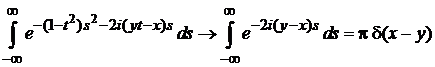где учено

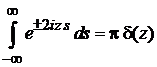. (2.24)

Из (П.4.20а) получаем условие полноты базиса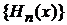

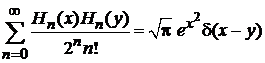. (П.4.21)

Для базиса функций гармонического осциллятора 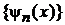, где

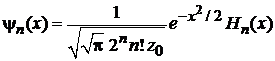, (6.32)

получаем условие полноты

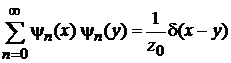. (П.4.22)

Обобщенные полиномы Лагерра

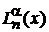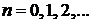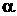, ; – любое число; .

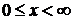Набор полиномов образует ортонормированный базис на полуоси .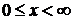

Используются:

· в теории измерительной техники и в теории систем связи;

· в квантовой механике описывают радиальное движение электрона в атоме.

Полиномы 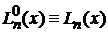исследовал Эдмон Никола Лагерр в 1878 г.

Обобщенные полиномы 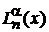изучал Николай Яковлевич Сонин в 1880 г., поэтому их называют также полиномами Сонина–Лагерра.

Уравнение Лагерра

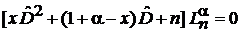(6.41)

является гипергеометрическим уравнением.

Формула Родрига

Методом факторизации ранее получена весовая функция

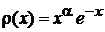. (П.3.9)

Из (П.3.10) при

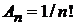
находим

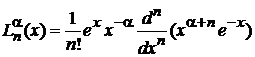. (6.42)

Полиномы низших степеней

Из (6.42) и (6.44) получаем:

,

,

,

.

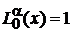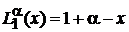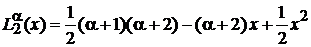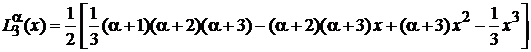При :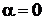

,

,

,

.

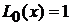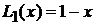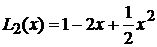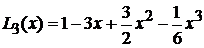Производящая функция

Методом факторизации ранее получено

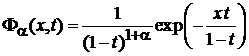. (6.52)

По определению

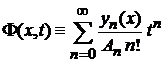(5.14)

с учетом 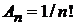получаем

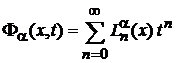. (6.53)

Рекуррентные соотношения

1. Дифференцируем по x (6.52)

.

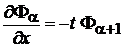Подставляем (6.53)

.

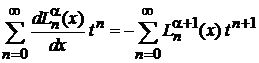Приравниваем коэффициенты при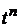

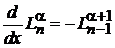. (6.54)

Следует

.

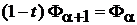Подставляем

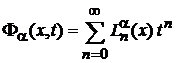, (6.53)

получаем

.

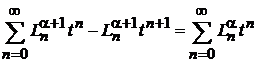Приравниваем коэффициенты при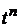

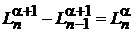. (6.59)

Из (6.58) в виде

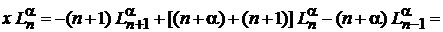
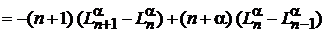
С учетом (6.59)

,

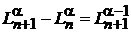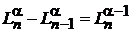
Получаем

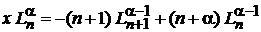. (6.60)

Заменяем 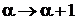и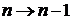

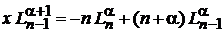. (6.61)

Из (6.58) в виде

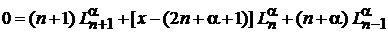
вычитаем (6.61) и получаем

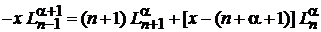. (6.64)

Условие ортонормированности

Методом факторизации ранее получено (П.3.11). Доопределяем 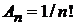и получаем

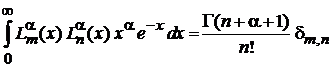. (6.67)

Подставляем

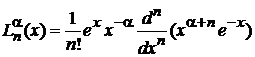, (6.42)

интегрируем по частям n раз, находим коэффициент

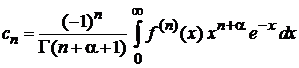. (6.69)

Упрощаем уравнение

Вводим боровский радиус

.

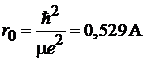Заменяем 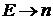– безразмерная величина:

,

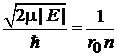тогда

.

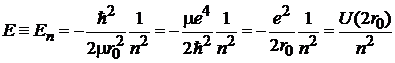Будет доказано, что n квантуется – 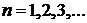, тогда получаем дискретный спектр

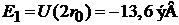– основное состояние,

,

.

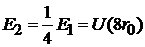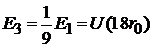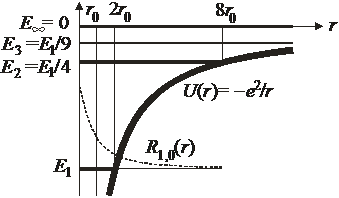
Исходное уравнение

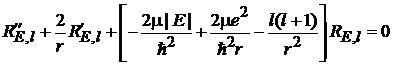(6.84)

получает вид

, .

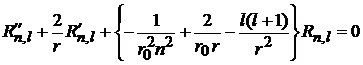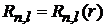Переходим к безразмерной x

, , , .

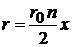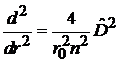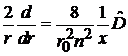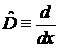Уравнение умножаем на 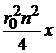и получаем

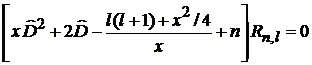, (6.85)

, .

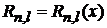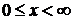Физический смысл параметров

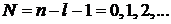
– радиальное квантовое число, равное числу нулей радиальной части волновой функции;

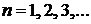
– главное квантовое число определяет энергию электрона

;

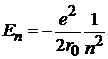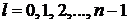
– орбитальное квантовое число определяет модуль момента импульса электрона

;

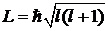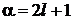
– число проекций на ось z орбитального момента с числом l.

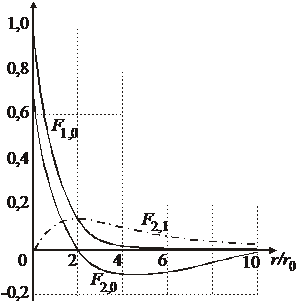
Решения 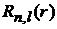низших порядков:

;

,

.

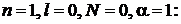
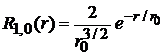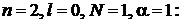
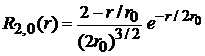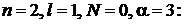
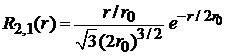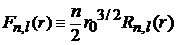
Рекуррентные соотношения

1. Равенство для полиномов Лагерра с одинаковыми порядками α

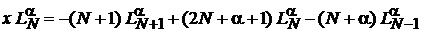(6.58)

умножаем на 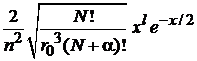и с учетом

, ,

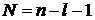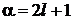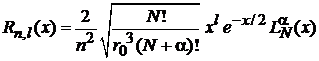(6.87)

получаем соотношение между функциями с одинаковыми l

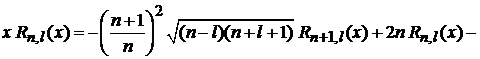
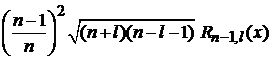– . (6.89)

Дважды используем

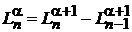, (6.59)

Находим

,

.

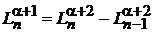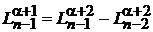В результате

.

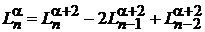Заменяем

, ,

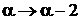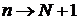Получаем

.

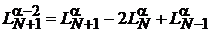Умножаем равенство на

,

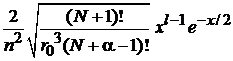И сравниваем с

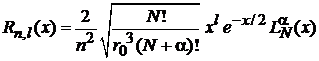, (6.87)

приходим к соотношению, где индекс l у функции, стоящей слева, на единицу меньше, чем у функций, стоящих справа:

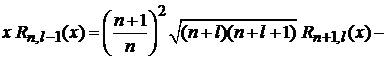
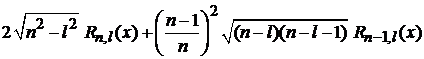– . (6.90)

Частные случаи

1. При 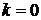из

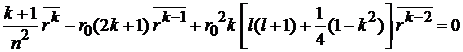, (П.5.10)

находим

,

,

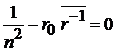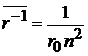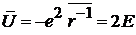
– теорема вириала связывает полную энергию со средним значением потенциальной энергии .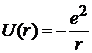

2. При 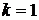получаем

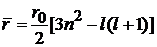. (П.5.8)

3. При 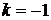находим

.

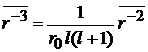Соотношение (П.5.10) не позволяет найти .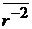

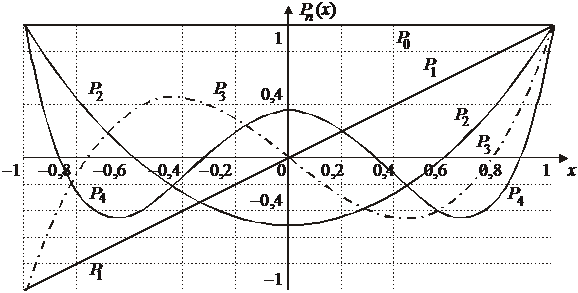
Полиномы Лежандра

, ; ; ;

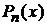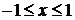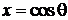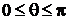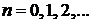
– описывают угловую зависимость в полярных и сферических координатах;

– входят в собственные функции оператора момента импульса и оператора Лапласа;

– множество 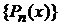образует ортонормированный базис на интервале .

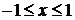Полиномы исследовал Андре Мари Лежандр в 1785 г.

Уравнение Лежандра

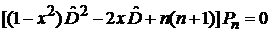, (6.93)

Учитываем

,

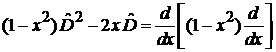тогда

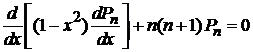. (6.93а)

Для угловой переменной

, ,

,

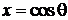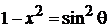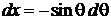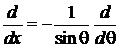
из (6.93а) для 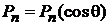получаем

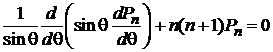. (6.94)

Метод факторизации

1. Уравнение

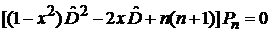(6.93)

гипергеометрического типа

.

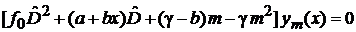2. Сравнение дает

,

, , , ,

, ,

,

,

, ,

,

.

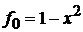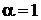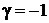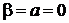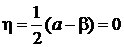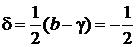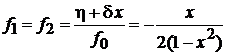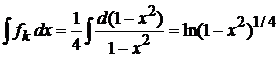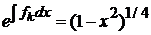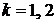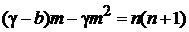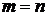3. Граничные условия

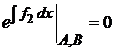в виде

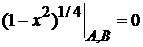
дают

, .

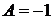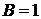4. Весовая функция

,

.

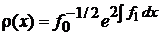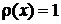5. Решение Родрига

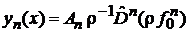дает

.

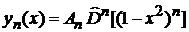Полагаем

,

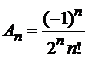получаем формулу Родрига дляполинома Лежандра

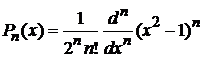. (6.96)

Свойство четности

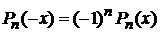, (6.97)

тогда

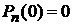, n – нечетное.

6. Ортонормированность

, .

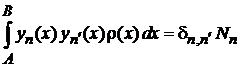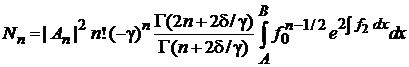Учитываем

, , ,

,

,

,

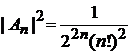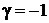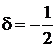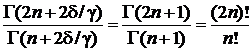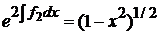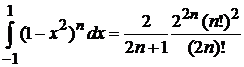тогда условие ортонормированности

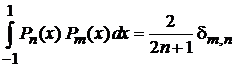. (6.112)

7. Производящая функция

,

,

.

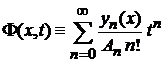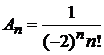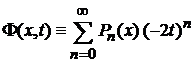Из уравнения для ξ

,

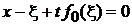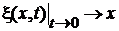в виде

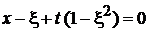
находим решение

,

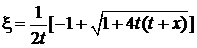которое при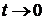

.

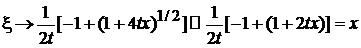Использовано

, .

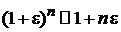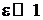Из

,

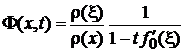с учетом

,

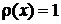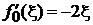
получаем

.

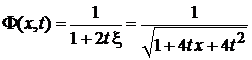Заменяем 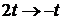, тогда

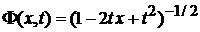, (6.101)

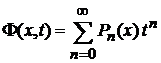. (6.102)

Полиномы низших порядков

Из

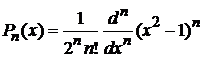, (6.96)

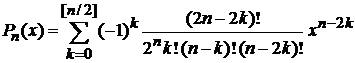(6.98)

находим

,

,

,

,

.

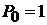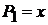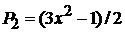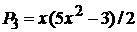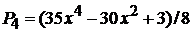Рекуррентные соотношения

Используем производящую функцию