Двойной интеграл в полярных координатах
Нам хорошо известны роль и значение метода замены переменной в определенном интеграле.
Аналогичный метод замены переменных используется и при вычислении двойных интегралов. Рассмотрим частный случай – переход к полярным координатам 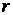 и
и 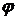 .
.
Прямоугольные координаты связаны с полярными следующими соотношениями:
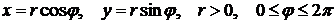 .
.
Пусть мы имеем двойной интеграл 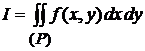 , где функция
, где функция 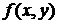 непрерывна в замкнутой области
непрерывна в замкнутой области  . Будем считать, что граница этой области пересекается каждой прямой, проходящей через начало
. Будем считать, что граница этой области пересекается каждой прямой, проходящей через начало
Координат не более, чем в двух точках. Имеет место формула замены переменных в двойном интеграле при переходе к полярным координатам:
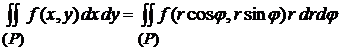 . (4.7)
. (4.7)
Далее, 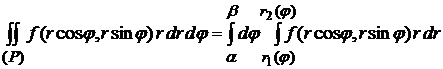 . (4.8)
. (4.8)
Заметим, что другой порядок интегрирования употребляется крайне редко, и мы на нем не будем останавливаться. Формула (4.8) соответствует случаю, когда полюс О лежит вне
области интегрирования  .
.
Если же полюс расположен внутри области  и любой луч, проведенный из полюса, пересекает границу области не более, чем в одной точке, то формула (4.8) примет вид:
и любой луч, проведенный из полюса, пересекает границу области не более, чем в одной точке, то формула (4.8) примет вид:
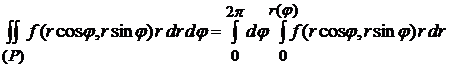 , (4.9)
, (4.9)
где 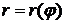 -- уравнение границы области
-- уравнение границы области  в полярных координатах.
в полярных координатах.
Площадь области  в полярных координатах вычисляется по формуле:
в полярных координатах вычисляется по формуле:
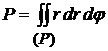 . (4.10)
. (4.10)
Замечание. При вычислении двойных интегралов переход от прямоугольных координат к полярным особенно полезен в том случае, когда область интегрирования  есть круг, или часть круга, или когда подынтегральная функция содержит в себе двучлен
есть круг, или часть круга, или когда подынтегральная функция содержит в себе двучлен 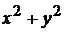 (при переходе к полярным координатам двучлен
(при переходе к полярным координатам двучлен 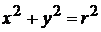 ).
).
Пример 4.7. Вычислить 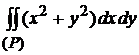 , где
, где  -- круг, ограниченный окружностью
-- круг, ограниченный окружностью 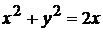 .
.
Круг  ограничен окружностью
ограничен окружностью 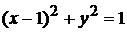 . Уравнение этой окружности в полярных координатах
. Уравнение этой окружности в полярных координатах
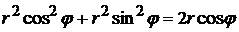 ,
,
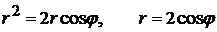 . По формулам (4.7) и (4.8) получаем
. По формулам (4.7) и (4.8) получаем
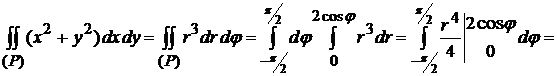
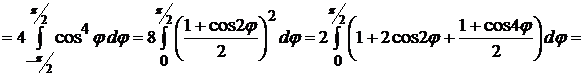
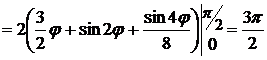 .
.
Пример 4.8. Найти площадь области, ограниченной лемнискатой 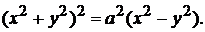
Так как 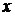 и
и 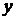 входят в уравнение только в четных степенях, то кривая симметрична относительно осей координат. Поэтому можно вычислить площадь части фигуры, расположенной в первой четверти, и результат умножить на 4:
входят в уравнение только в четных степенях, то кривая симметрична относительно осей координат. Поэтому можно вычислить площадь части фигуры, расположенной в первой четверти, и результат умножить на 4: 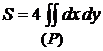 .
.
Здесь выгодно перейти к полярным координатам, так как в уравнение кривой входит выражение 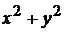 . Уравнение лемнискаты в полярных координатах
. Уравнение лемнискаты в полярных координатах 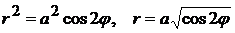 .
.
Для области 
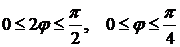 и
и 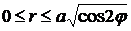 .
.
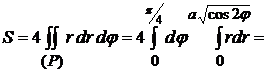
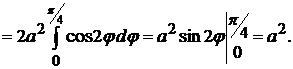
Упражнения
Вычислить площади фигур, ограниченных линиями ( в скобках указаны ответы).
1) 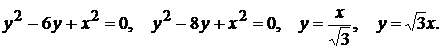
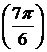
2) 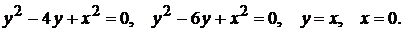
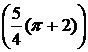
3) 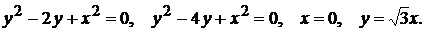
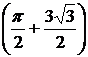
4) 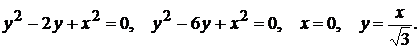
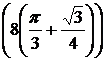
5) 
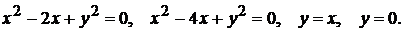
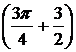
6) 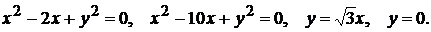
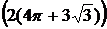
7) 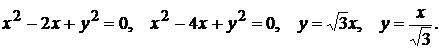

8) 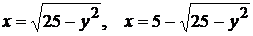
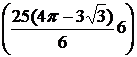
9) 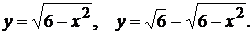
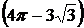
10) 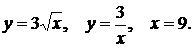
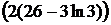
11) 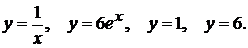 (5)
(5)
12) 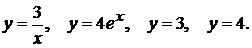 (1)
(1)
Найти объемы тел, ограниченных поверхностями:
13) 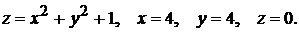
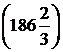
14) 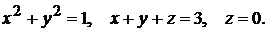
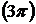
15) 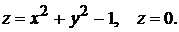

16) 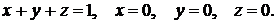
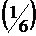
17) 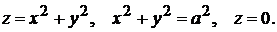
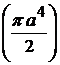
18) 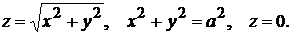
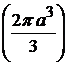
Литература
1. Кудрявцев Л.Д. Математический анализ, Т.1,2.—М.: Высшая школа 1973
2. Фихтенгльц Г.М. Курс дифференциального и интегрального исчисления, Т. 2,3, Физматгиз, 1969
3. Демидович Б.П. Сборник задач по курсу математического анализа. – М.: Наука, 1972
4. Виноградова И.А., Олехник С.Н., Садовничий В.А. Математический анализ в задачах и упражнениях: учебное пособие. –М.: Изд-во Моск. ун-та, 1991
5. Абанин А.В., Моржаков В.В., Спинко Л.И. Кратные интегралы. Методические указания к практическим занятиям по курсу «Математический анализ».-- Ростов-на-Дону, 1985
6. Берман Г.Н. Сборник задач по курсу математического анализа.—М.: Наука, 1971

