Разработка урока по алгебре и началам анализа по теме: «Интеграл»

Разработка урока по алгебре и началам анализа по теме: «Интеграл»

Цели:

1. Сформировать способность у студентов к вычислению интегралов функций (линейной, степенной, тригонометрических функций).

2. Тренировать способность у студентов к вычислению интегралов функций (линейной, степенной, тригонометрических функций).

В результате изучения темы студент должен знать:

свойства и формулы для вычисления интегралов;

В результате изучения темы студент должен уметь:

1) владеть свойствами и формулами для вычисления интегралов.

2) различать ситуации, какое из свойств и какую формулу целесообразнее применить при решении конкретной задачи.

Тип урока: обобщения и систематизации.

Задачи:

1. Решение задач на вычисление интегралов.

2. Решение задач на отыскание ошибок в предложенном решении

Ход урока

Адаптивный этап

Самостоятельная работа

Самостоятельно выберите и выполните предложенные ниже задачи.

Разноуровневые задания помогут определить вашу готовность к восприятию новой темы и самостоятельному открытию знаний. Не огорчайтесь, если у вас возникли затруднения, смело открывайте раздел «Полезные советы», который находится на странице, указанной после заданий, и сравните своё решение с предложенным эталоном. Желаем удачи!

Разноуровневые задания

Вычислить неопределенные интегралы

1 уровень	2уровень	3 уровень

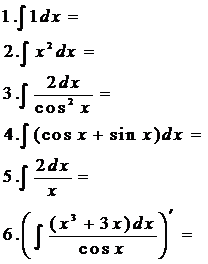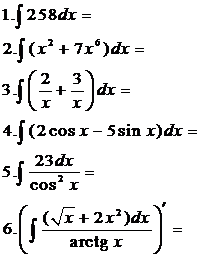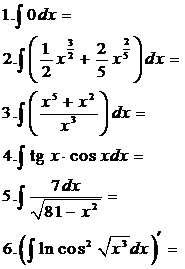Ответы и указания к решению, вы найдете в разделе «Полезные советы».

Таблица 4

Карточка анализа индивидуального задания

Символы, которые необходимо использовать при анализе индивидуального задания:

Задание выполнено: ставится + или -

Трудности вызваны:

ставится знак +, если вы согласны с предложенным затруднением;

?, если вы не уверены в этом;

-, если вы этого не испытали.

Продолжение Таблицы 4

1 уровень	2 уровень	3 уровень
Задание выполнено:
Трудности вызваны:
Неумением использовать формулы для нахождения интегралов линейной функции	Неумением использовать формулы для нахождения интегралов линейной функции	Неумением использовать формулы для нахождения интегралов линейной функции
Неумением использовать формулы для нахождения интегралов степенной функции	Неумением использовать формулы для нахождения интегралов степенной функции	Неумением использовать формулы для нахождения интегралов степенной функции
Неумением использовать формулы для нахождения интегралов тригонометрических функции	Неумением использовать формулы для нахождения интегралов тригонометрических функции	Неумением использовать формулы для нахождения интегралов тригонометрических функции
Неумением использовать свойства интегралов	Неумением использовать свойства интегралов	Неумением использовать свойства интегралов

Нормативный этап

Уровень

Для функции 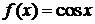найти первообразную, график которой проходит через точку М(0;2).

Уровень

Вычислить интеграл 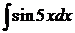, используя замену.

Уровень

Вычислить интеграл 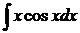, используя…

Ответы и указания к решению, вы найдете в разделе «Полезные советы».

Прикладной этап

Ответы и указания к решению, вы найдете в разделе «Полезные советы».

Полезные советы

Свойства интегралов

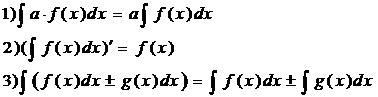
Эталон решения разноуровневых учебных задач ([1-6] – формулы, (1-3) свойства)

Уровень

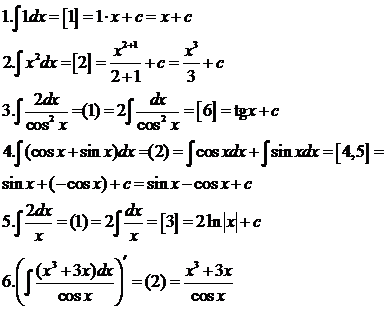
Уровень

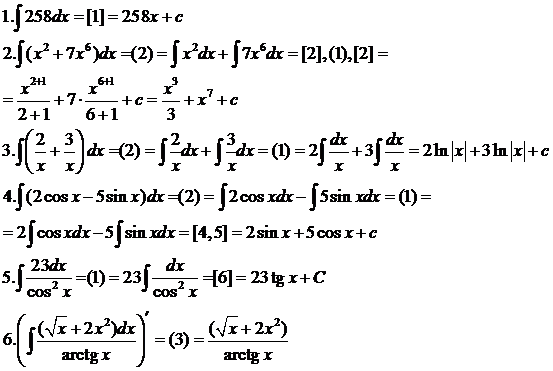
Уровень

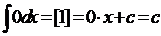
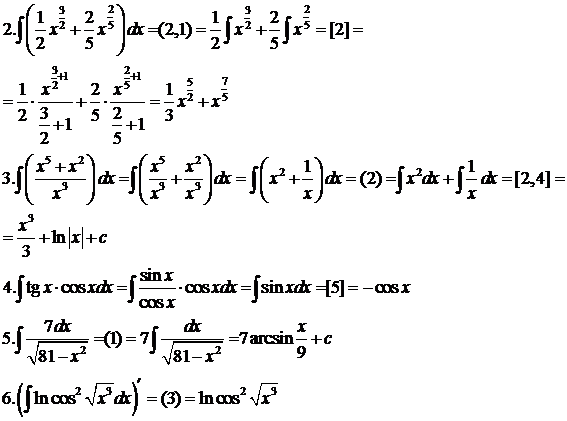
Уровень

Уровень

Введем замену переменной х

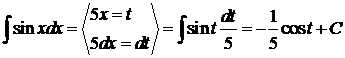
Уровень

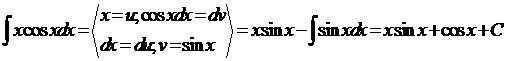
Уровень

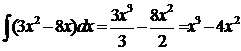
Уровень

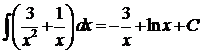
Уровень

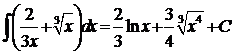
Таким образом, происходит выявление затруднений и самоанализ своей деятельности на уроке.

Разработка урока по алгебре и началам анализа по теме: «Интеграл»

Цели:

1. Сформировать способность у студентов к вычислению интегралов функций (линейной, степенной, тригонометрических функций).

2. Тренировать способность у студентов к вычислению интегралов функций (линейной, степенной, тригонометрических функций).

В результате изучения темы студент должен знать:

свойства и формулы для вычисления интегралов;

В результате изучения темы студент должен уметь:

1) владеть свойствами и формулами для вычисления интегралов.

2) различать ситуации, какое из свойств и какую формулу целесообразнее применить при решении конкретной задачи.

Тип урока: обобщения и систематизации.

Задачи:

1. Решение задач на вычисление интегралов.

2. Решение задач на отыскание ошибок в предложенном решении

Ход урока

Адаптивный этап

Самостоятельная работа

Самостоятельно выберите и выполните предложенные ниже задачи.

Разноуровневые задания помогут определить вашу готовность к восприятию новой темы и самостоятельному открытию знаний. Не огорчайтесь, если у вас возникли затруднения, смело открывайте раздел «Полезные советы», который находится на странице, указанной после заданий, и сравните своё решение с предложенным эталоном. Желаем удачи!

Разноуровневые задания

Вычислить неопределенные интегралы

1 уровень	2уровень	3 уровень

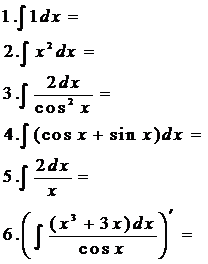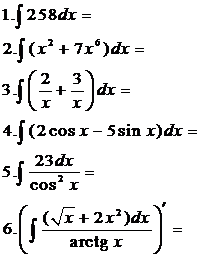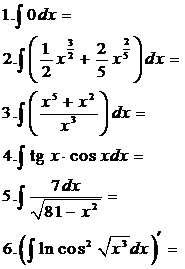Ответы и указания к решению, вы найдете в разделе «Полезные советы».

Таблица 4

Карточка анализа индивидуального задания

Символы, которые необходимо использовать при анализе индивидуального задания:

Задание выполнено: ставится + или -

Трудности вызваны:

ставится знак +, если вы согласны с предложенным затруднением;

?, если вы не уверены в этом;

-, если вы этого не испытали.

Продолжение Таблицы 4

1 уровень	2 уровень	3 уровень
Задание выполнено:
Трудности вызваны:
Неумением использовать формулы для нахождения интегралов линейной функции	Неумением использовать формулы для нахождения интегралов линейной функции	Неумением использовать формулы для нахождения интегралов линейной функции
Неумением использовать формулы для нахождения интегралов степенной функции	Неумением использовать формулы для нахождения интегралов степенной функции	Неумением использовать формулы для нахождения интегралов степенной функции
Неумением использовать формулы для нахождения интегралов тригонометрических функции	Неумением использовать формулы для нахождения интегралов тригонометрических функции	Неумением использовать формулы для нахождения интегралов тригонометрических функции
Неумением использовать свойства интегралов	Неумением использовать свойства интегралов	Неумением использовать свойства интегралов

Нормативный этап