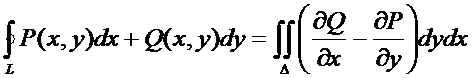Вычисление тройного интеграла в цилиндр. координатах.

Зададим в трехмерном пространстве прямоугольную систему координат x, y, z. Произвольная точка М(x, y, z) пространства определяется также тройкой чисел (r, q, z), где z – по-прежнему ее аппликата, а (r, q) – полярные координаты точки (x, y) плоскости Oxy в предположении, что полярная ось совпадает с положительным направлением оси Ох. Очевидно:

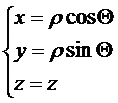
Координатные поверхности в рассматриваемом случае будут якобианом этого преобразования:

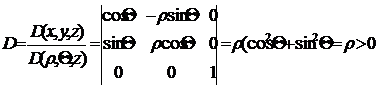Исключая случай r=0, якобиан>0.

1. r=const – цилиндрические поверхности с образующими параллельными оси z. Направ­ля­ю­щими для них служат окружности на плоскости ху с центром в начале координат;

2. q=const – полуплоскости, проходящие через ось z;

3. z=const – плоскости параллельные плоскости ху.

Формула замены переменных в этом случае имеет вид:

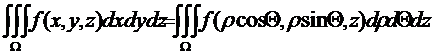Чтобы наглядно получить элемент объема в цилиндрических координатах рассмотрим элементарную область в пространстве (x, y, z), ограниченную двумя цилиндрическими поверхностями радиусов r и r+dr, двумя горизонтальными плоскостями, лежащими на высотах z и z+dz и двумя полуплоскостями, проходящими через ось z и наклоненными к плоскости xz под углами q и q+dq. Элемент пространства, ограниченный этими поверхностями, с точностью до бесконечно малых высшего порядка, представляет собой прямоугольный параллелепипед с ребрами dr, rdq, dz. Его объем равен rdrdqdz.

Приложение тройного интеграла.

Криволинейный интеграл 1-го рода, их св-ва и выч..

Если при стремлении к нулю шага разбиения кривой на частичные отрезки существует предел интегральных сумм, то этот предел называется криволинейным интегралом от функции f(x, y, z) по длине дуги АВили криволинейным интегралом первого рода.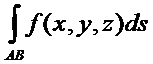

Кривол. интеграл по длине дуги АВ находиться формуле: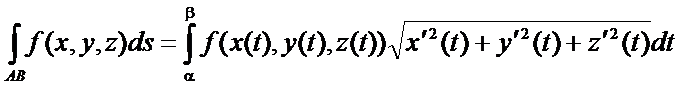

1) Значение интеграла по длине дуги не зависит от напр. кривой АВ.

2) Постоянный множитель можно выносить за знак крив. интеграла.

3) Криволинейный интерал от суммы функций равен сумме криволинейных интегралов от этих функций.

4) Если кривая АВ разбита на дуга АС и СВ, то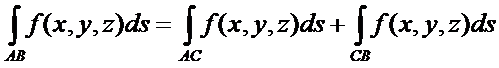

5) Если в точках кривой АВ 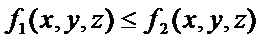то

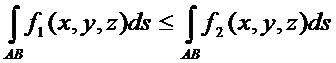
6) Справедливо неравенство: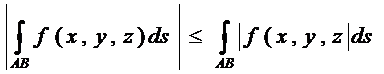

Пример. Вычислить интеграл 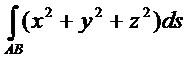по одному витку винтовой линии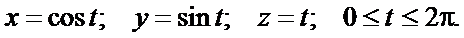

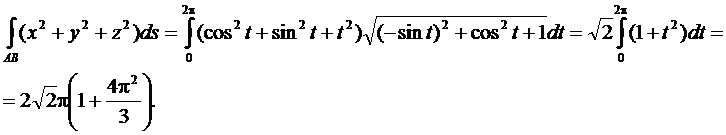
Приложения криволинейный интеграл 1-го рода.

Криволинейный интеграл 2-го рода, их св-ва и выч..

Если при стремлении к нулю шага разбиения кривой АВ интегральные суммы имеют конечный предел, то этот предел называется криволинейным интегралом по переменной х от функции P(x, y, z) по кривой АВ в направлении от А к В.

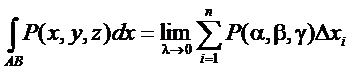
Сумму криволинейных инт. криволинейным инт. второго рода.

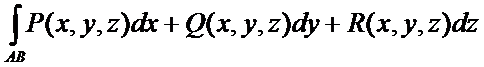
1)

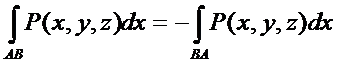
2)

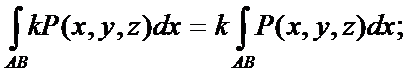
3)

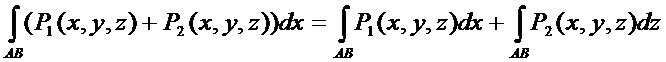
4)

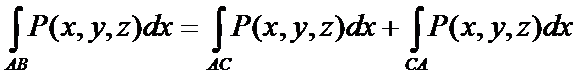
5) Криволинейный инт. по замкнутой кривой L от направления обхода кривой.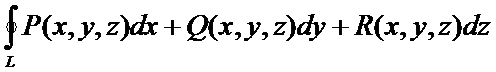

Вычисление криволинейных интегралов второго рода

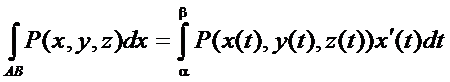
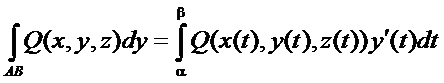
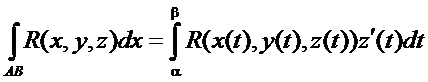
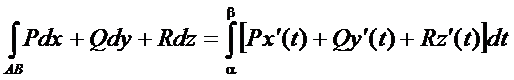
Формула Грина.

Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.

Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.

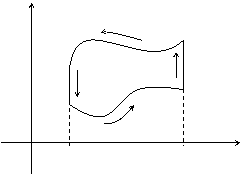y

y = y₂(x)

D

A

C

B

y= y₁(x)

0 x₁ x₂ x

Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде: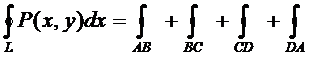

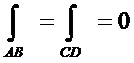
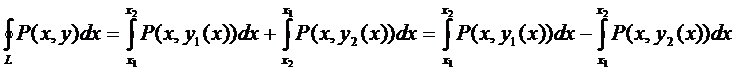
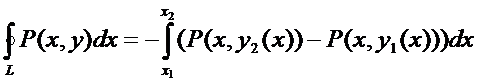
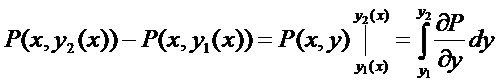
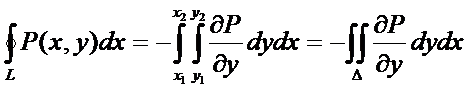
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования