Определенный интеграл как предел интегральных сумм. Геометрический и экономический смысл

Пусть функция у=f(х) определена на отрезке [а; b], а < b. Выполним следующие действия.

1. С помощью точек х_о=а, х₁ ,х₂, …, х_n=bразобьем отрезок [а; b] на n частичных отрезкoв [х_о; х₁], [х₁; х₂], …, [x_n-1; x_n].

2. В каждом чacтичном отрезке [x_i-1; x_i], i= 1,2,…, n выберем произвольную точку c_i 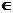[x_i-1; x_i] и вычислим значение функции в ней, т. е. величину f(c_i).

3. Умножим найденное значение функции f(c_i) на длину 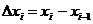соответствующего частичного отрезка: f(c_i)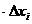

4. Составим сумму S_n всех таких произведений:

S_n= f(c_i) 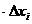+ f(c_i) 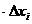+…+ f(c_i) 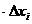= 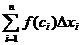(1)

Сумма вида (1) называется uнтегралънoй суммой функции у=f(х) на отрезке [а; b]. Обозначим через λ длину наибольшего частичного отрезка: 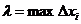(i = 1,2, ... ,n).

5. Найдем предел интегральной суммы (1), когда n 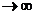что .

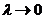Если при этом интегральная сумма S_n имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = f(x) на отрезке [а; b] и обозначается 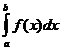. Таким образом,

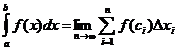. (2)

Числа а и b называются соответственно нижним и верхним пределом интегрирования, f(x) – подынтегральной функцией, f(x)dx – подынтегральным выражением, х – переменной интегрирования, отрезок [а; b] –областью (отрезком) интегрирования

Функция у = f(x), для которой на отрезке [а; b] существует определенный интеграл 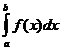, называется интегрируемой на этом отрезке.

Сформулируем теорему существования определенного интеграла.

Теорема (Коши). Если функция у = f(x) непрерывна на отрезке [а; b], то определенный интеграл 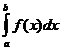существует.

Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.

Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (2).

1. Определенный интеграл не зависит от обозначения переменной интегрирования.

= =

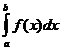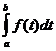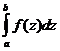
Это следует из того, что интегральная сумма (1), а, следовательно, и ее предел (2) не зависят от того, какой буквой обозначается аргумент данной функции.

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

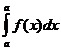=0.

3. Для любого действительного числа с: .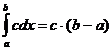

Площадь криволинейной трапеции. Пусть на отрезке [a;b] задана непрерывная функция у = f(x) 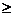0. Фигура, ограниченная сверху графиком функции у = f(x) , снизу - осью Ох, сбоку - прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.

Для этого отрезок [a;b]точками a = x₀, x₁, …, b=x_n (x₀ < x₁ < … < x_n) разобьем на n частичных отрезков [x₀,x₁], [x₁;x₂], …, [x_n-1;x_n]. В каждом частичном отрезке [x_i-1;x_i] (i=1,2,…n) возьмем произвольную точку с_i и вычислим значение функции в ней, т. е. f(c_i). Умножим значение функции f(c_i) на длину 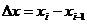соответствующего частичного отрезка. Произведение f(c_i) 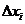равно площади прямоугольника с основанием 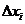и высотой f(c_i). Сумма всех таких произведений

f(c₁) 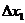+ f(c₂) 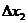+ … + f(c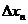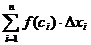_n) = =S_n

равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

S ≈ S_n =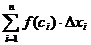

С уменьшением всех величин 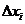точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры S_n, когда n неограниченно возрастает так, что :

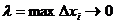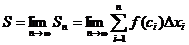, то есть .

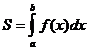Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

В этом и состоит геометрический смысл определенного интеграла.

Экономический смысл интеграла. Пусть функция z=f(t) описывает изменение производительности с течением времени. Найдем объем продукции и, произведенной за промежуток времени [0,Т].

Отметим, что если производительность не изменяется с течением времени (f(t) - постоянная функция), то объем продукции 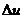, произведенной за некоторый промежуток времени [t, t+ 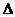t], задается формулой 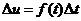. В общем случае справедливо приближенное равенство 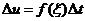, где 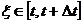, которое оказывается тем более точным, чем меньше 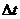. Разобьем отрезок [0,Т] на промежутки времени точками: 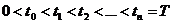. Для величины объема продукции 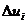, произведенной за промежуток времени 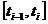, имеем 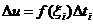, где 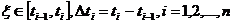. Тогда

.

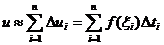При стремлении 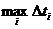к нулю каждое из использованных приближенных равенств становится все более точным, поэтому

.

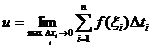Учитывая определение определенного интеграла, окончательно получаем

,

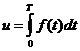т.е. если f(t) – производительность труда в момент t, то 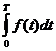есть объем выпускаемой продукции за промежуток [0,Т].

Сравнение данной задачи с задачей о площади криволинейной трапеции показывает, что величина и объем продукции, произведенной за промежуток времени [0,Т], численно равна площади под графиком функции z=f(t), описывающей изменение производительности труда с течением времени, на промежутке [0,T] или 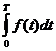.