Метод введения новой переменной

Методическое пособие

ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ ИНЖЕНЕРНЫХ И ЭКОНОМИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ

ОРЕЛ 2009

УДК

Рецензенты:

А.Г. Филонов — кандидат физико-математических наук, профессор,;

И.И. Зубова — кандидат педагогических наук, доцент кафедры физики Орловского государственного аграрного Университета.

Уварова, М.Н., Павлова Т.А. Неопределенный и определенный интегралы. Приложения определенного интеграла: методическое пособие / М.Н. Уварова, Т.А. Павлова. /.Изд. 1-е. — Орел: изд-во «Картуш», 2009. —___с.

ISBN

Печатается по решению методической комиссии факультета гуманитарных и естественнонаучных дисциплин Орел ГАУ (протокол №____)

Предлагаемое методическое пособие предназначено для самостоятельной работы студентов, а также преподавателей при проведении лекционных и практических занятий по математике.

Содержание

Введение. 4

Понятие неопределенного интеграла, его свойства. Таблица интегралов. Непосредственное интегрирование. 5

Метод введения новой переменной. 10

Метод интегрирования по частям. 13

Интегрирование рациональных функций. 16

Интегрирование тригонометрических функций. 21

Интегрирование иррациональных функций. 25

Определенный интеграл как предел интегральных сумм. Геометрический и экономический смысл. 30

Свойства определенного интеграла. 32

Интеграл с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница. 33

Вычисление определенных интегралов. 35

Несобственные интегралы.. 36

Несобственные интегралы с бесконечными пределами интегрирования 36

Несобственные интегралы от неограниченных функций. 37

Приложения определенного интеграла. 38

Геометрические приложения определенного интеграла. 38

Вычисление площадей плоских фигур. 38

Вычисление длины дуги. 40

Нахождение объёма тела по площадям поперечных сечений. 42

Вычисление объемов тел вращения. 43

Площадь поверхности вращения. 44

Приложения определенного интеграла к решению некоторых задач механики и физики. 45

Использование понятия определенного интеграла в экономике. 51

Тест 1. 54

Тест 2. 55

Тест 3. 56

Набор заданий для выполнения расчетно-графической работы.. 65

Формулы. Справочный материал. 87

Литература. 98

Введение

Методическое пособие предназначено для организации самостоятельной работы студентов инженерных и экономических специальностей. Оно полезно при подготовке к модулю по данной теме, решении расчетно-графической работы, а также вырабатывать умение применять полученные знания при решении задач прикладного характера.

Цель данного методического пособия является активизация процесса обучения и повышение его эффективности.

Каждая тема включает в себя необходимый теоретический материал, который сопровождается большим количеством примеров с решениями, а также задачи и вопросы для самоконтроля. При работе с пособием следует обратить внимание на рекомендации. Их необходимо изучить и использовать при решении задач.

Знаком * отмечены задания повышенной сложности.

Понятие неопределенного интеграла, его свойства. Таблица интегралов. Непосредственное интегрирование

Понятие интеграла (наряду с понятиями производной и дифференциала) является фундаментальным понятием математического анализа. Возникновение этого понятия связано с необходимостью решать задачи на вычисление площадей фигур, длин кривых, объемов тел, работы переменной силы и т. д., а также находить функции по их производным.

Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке, если для всех х из этого промежутка выполняется равенство .

Примеры.

1. F(x) = sin x является первообразной для f(x) = cos x на множестве , так как для любого .

2. Если , то , так как .

Если F(x) есть одна из первообразных для функции f(x), то любая функция семейства F(x)+C, где С – постоянное число, является первообразной для f(x).

Очевидно, что верно и обратное: каждая функция, первообразная для f(x), может быть представлена в этой форме.

Определение 2. Если F(x) – первообразная для f(x), то выражение F(x)+C, где С – произвольная постоянная, называется неопределенным интегралом от f(x) и обозначается:

f(x)dx = F(x) + C (1)

Функция f(x) называется подынтегральной функцией, произведение f(x)dx — подынтегральным выражением, x — переменной интегрирования.

Заметим, что символ f(x)dx ввел в 1675 году знаменитый немецкий математик Г. В. Лейбниц (1646 – 1716).

Примеры.

1. 2. 3. .

Рекомендация. Проверка правильности результата интегрирования осуществляется дифференцированием последнего. После дифференцирования должна получаться подынтегральная функция.

Таблица основных интегралов

I.

II.

III.

IV. .

V.

VI. < .

VII.

VIII.

IX. .

X.

XI.

XII.

XIII.

Обоснование формул может быть произведено одним и тем же путем: достаточно убедиться, что производная правой части равна подынтегральной функции левой части.

Важно таблицу основных интегралов, как и таблицу производных основных элементарных функций, знать наизусть.

Простейшие правила интегрирования

А. где а=const, т.е. постоянный множитель, можно выносить за знак интеграла.

В. т.е. интеграл от алгебраической суммы функций, равен алгебраической сумме интегралов от этих функций.

С.

Вычисление интегралов путем использования таблиц основных интегралов и указанных правил называется непосредственным интегрированием.

Найти интегралы.

1.

2.

3.

4.

5.

6.

7.

8.

Примеры.

1.

Представляем каждое слагаемое в виде степени и интегрируем сумму степеней:

.

2.

Представим дробь в виде суммы и интегрируем:

3.

Возведем разность в квадрат и затем интегрируем:

Найти интегралы.

9.

10.

11. , (a,b,c – постоянные).

12.

Метод непосредственного интегрирования требует определенных навыков в преобразованиях подынтегральных функций.

Примеры.

1.

Числитель дроби представим в виде разности кубов, дробь сократим.

.

2.

Прибавим и вычтем в числителе и представим в виде суммы двух слагаемых:

3.

Так как , то

Заметим, что возможно и другое решение. Так как , то

,

поэтому

(Применили табличный интеграл VII и правило С.)

Как видим, при решении одного и того же примера могут получаться разные формы ответов. Но оба они являются правильными, что легко проверить дифференцированием.

Найти интегралы.

13.

14.

15.

16.

17.

Сравните ответы и подынтегральные функции примеров 13 и 17.

В таблице интегралов предполагалось, что х есть независимая переменная. Однако эта таблица полностью сохраняется, если х заменить любой функцией от независимой переменной. Интеграл запишется так:

,

где — дифференцируемая функция.

Выбирая различным образом функцию , мы можем расширить область применения таблицы интегралов.

Пример.

Из формулы XI следует:

Заменяя здесь х на , получим , т.е.

.

Аналогично , т.е. .

На этом основано решение интегралов подведением под знак дифференциала.

Примеры:

1. .

Заметим, что , помножим на 3, а интеграл – на 1/3. Получим

2. .

Чтобы воспользоваться формулой XIII, выполним преобразования:

.

3. .

Найдем , помножим в подынтегральном выражении на 3, а интеграл на 1/3:

.

Заметим, что тот же результат следует из правила С.

Найти интегралы.

18.

19.

20.

21.

22.

Вопросы и задания для самоконтроля*

1. Приведите 5 примеров к определениям 1 и 2.

2. Найдите первообразную для функции при х<0.

3. Докажите формулы II и III.

4. Объясните, почему функция arcsin x и –arccos x имеют одинаковые производные?

5. *Для всякой ли функции существует первообразная или неопределенный интеграл?

6. *Каков геометрический смысл неопределенного интеграла?

7. Запишите таблицу основных интегралов I – XIII для случая сложной функции.

Ответы.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

61.

62.

63.

64.

65.

66.

67.

68.

69.

70.

71.

72.

73.

74.

75.

76.

77.

78.

79.

80.

81.

82.

83.

84.

85.

86.

Формула Ньютона-Лейбница

Опираясь на свойства интеграла с переменным верхним пределом, получили основную формулу интегрального исчисления.

Теорема. Пусть функция у = f(x) непрерывна на отрезке[a, b] и F(x) – любая первообразная для f(x) на [a, b]. Тогда определенный интеграл от функции f(x) на [a, b] равен приращению первообразной F(x) на этом отрезке, т.е.

. (10)

Доказательство: Пусть F(x) – некоторая первообразная для функции f(x). Но по теореме 2 функция Ф(х),заданная формулой Ф(х) = = , также является первообразной для функции f(x), и найдется такое число C, что F(x) = Ф(x) + C. Тогда для приращения первообразной имеем

F(b) – F(a) = (Ф(b)+C) – (Ф(a)+C) =Ф(b) – Ф(а) = - .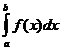

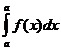Но . И тогда F(b) –F(a) = .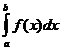

Нахождение определенных интегралов с использованием формулы Ньютона-Лейбница осуществляется в два шага: на первом шаге, используя технику нахождения неопределенного интеграла, находят некоторую первообразную F(x) для подынтегральной функции f(x); на втором применяется собственно формула Ньютона-Лейбница– находится приращение первообразной, равное искомому интегралу. В связи с этим, введем обозначение для приращения первообразной, которое удобно использовать при записи решений. По определению положим

.

Следует подчеркнуть, что при применении формулы Ньютона-Лейбница можно использовать любую первообразную F(x) для подынтегральной функции f(x), например, имеющую наиболее простой вид при С=0.

Несобственные интегралы

Вычисление длины дуги

1. Явное задание кривой. В этом случае кривая задается в виде , , и длина ее дуги равна L= .

2. Кривая в полярных координатах.Уравнение кривой имеет в этом случае вид и длина ее дуги равна L= .

3.Параметрическое задании кривой.Пусть функции x(t) и y(t) имеют на отрезке непрерывныепроизводные и . Тогда длина дуги кривой

L= .

Пример. Найдём длину дуги кривой (циклоиды), заданной на плоскости параметрическими уравнениями

лежащей между точками O(0;0) (соответствует 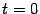) и A(2 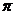a;0) (соответствует ).

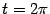Для функций f₁(t)=a(t-sint) и f₂(t)=a(1-cost) вычислим производные:

Тогда искомая длина дуги равна

Пример. Пусть линия на плоскости с полярными координатами (r; 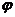) задана уравнением r=a 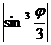(a>0). Поскольку функция f( 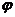)=a 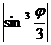периодична с периодом 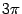, достаточно рассматривать только значения аргумента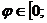 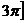, при которых выражение 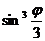неотрицательно. Кривая имеет вид, изображённый на следующем рисунке.

Найдём длину этой линии.

Имеем

Поэтому искомая дли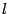на равна

Тест 1

1. При каких а и b функция 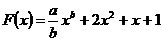является первообразной для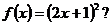

2. При каких целых а, b, c функция 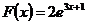является первообразной для функции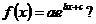

3. При каких целых а, b, c функци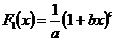и и 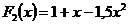является первообразными для одной и той же функции f(x)?

4. Найти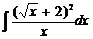

Ответ: 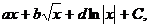где а, b, d – целые числа: а = …, b = …, d = … .

5. Найти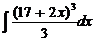

Ответ: 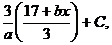где а, b, d – целые числа: а = …, b = …, d = … .

6. Найти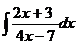

Ответ: 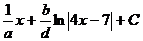где а, b, d – целые числа, дробь 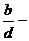несократима, 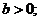а = …, b = …, d = … .

7. Найти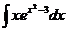

Ответ: 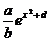где а, b, d – целые числа, дробь а/b - несократима, 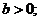а = …, b = …, d = … .

8. Найти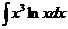

Ответ: 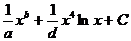где а, b, d – целые числа: а = …, b = …, d = … .

9. Найти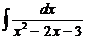

Ответ: 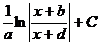где а, b, d – целые числа, 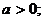а = …, b = …, d = … .

10. Найти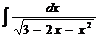

Ответ: 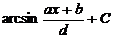где а, b, d – целые числа, 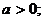а = …, b = …, d = … .

Тест 2

1. Найти максимальное значение интегральной суммы функции у = 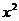на отрезке [0, 1],если число отрезков разбиения равно 4.

Ответ: a/b, где a = … , b = … (a и b – положительные целые числа, дробь a/b – несократима).

2. При каких целых значениях параметровa и b справедливо равенство ?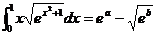

3. Найти такие целые значения a и b, при которых справедливо равенство: .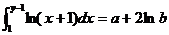

4. Вычислить определённый интеграл .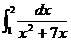

Ответ: 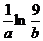, где а = … , b = …(a и b – целые числа).

5. При каком значении параметра а интеграл 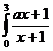dx равен площади S фигуры, ограниченной линиями 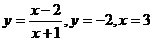.Найти эту площадь S.

Ответ: а = … , S = 9 – ln b, где b = … (a и b - целые числа).

6. Найти длину дуги кривой 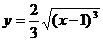на отрезке [1,4].

Ответ: a/b, где a = … , b = … (a и b – положительные целые числа, дробь a/b – несократима).

7. Найти объем тела, полученного при вращении вокруг оси абсцисс плоской фигуры, ограниченной линиями .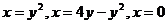

Ответ: аπ/3, где а = ….

8. При каком минимальном значении n формула трапеций обеспечивает вычисление определенного нтеграла 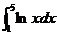с точностью до 0,001?

9. Найти площадь фигуры, заключенной между кривой 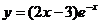и ее горизонтальной асимптотой на промежутке [0; +∞).

10. Вычислить определенный интеграл 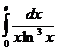,если он сходится.

Тест 3

I Интегрирование по частям

1.
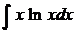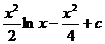2.
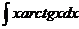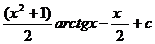3.
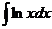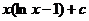4.
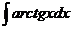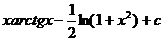5.
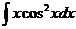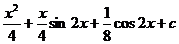6.
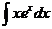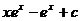7.
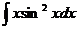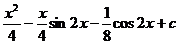8.
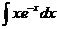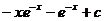9.
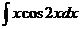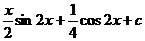10.
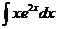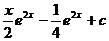11.
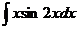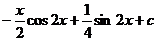12.
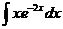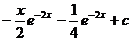13.
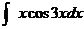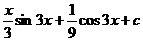14.
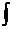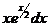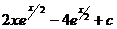15.
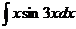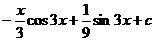16.
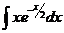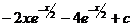17.
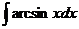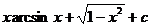18.
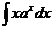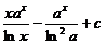19.
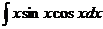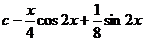20.
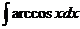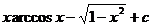21.
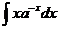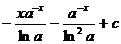22.
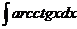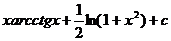23.
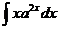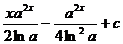24.
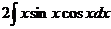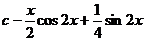25.
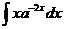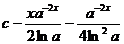26.
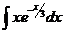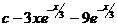27.
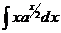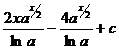28.
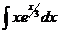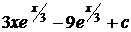29.
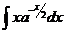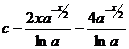30.

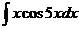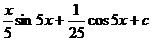II Иррациональные функции

1.
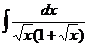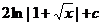2.
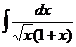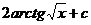3.
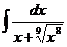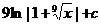4.
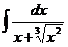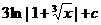5.
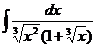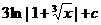6.
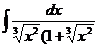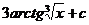7.
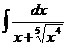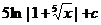8.
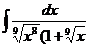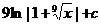9.
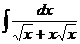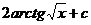10.
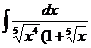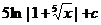11.
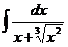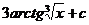12.
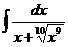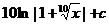13.
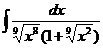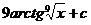14.
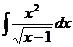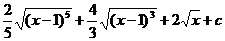15.
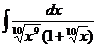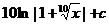16.
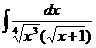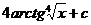17.
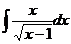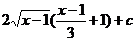18.
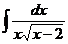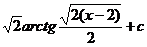19.
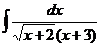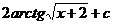20.
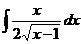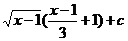21.
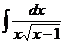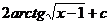22.
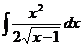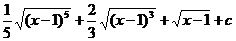23.
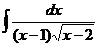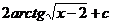24.
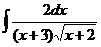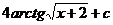25.
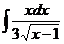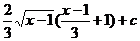26.
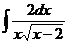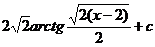27.
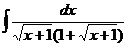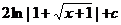28.
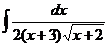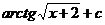29.
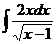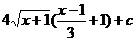30.

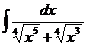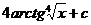III Универсальная подстановка

1)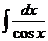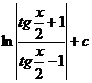
2)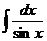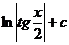
3)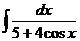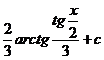
4)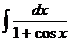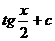
5)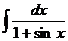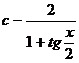
6)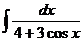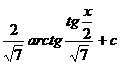
7)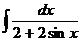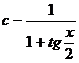
8)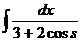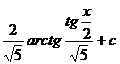
9)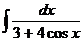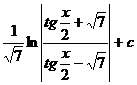
10)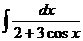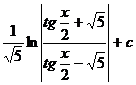
11)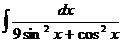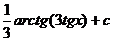
12)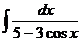