Уравнение Лемниската-Берлуни

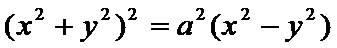
9. Вычисление длины дуги кривой. Пусть заданна 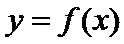на .

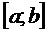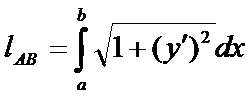
Объемы тел вращения

1.

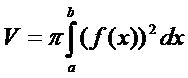
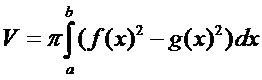
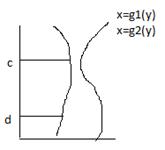
2.

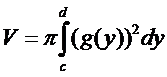
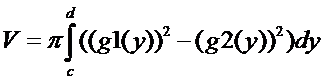
17.Несобственные(н/с) интегралы.

Интегралы с бесконечными пределами

А) н/с интеграл с бесконечным верхним пределом инт.

О1. У=f(x), хЄ[a;+¥) , где а- конечное число. Ф-ция f(x) и интегрируема на любом отрезке [а;B] Ì [a;+¥). (1) 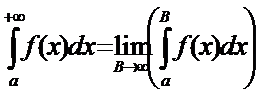--н/с интеграл с бесконечным верхним пределом

Иногда (1) называют н/с и. первого рода

О2. Если предел в правой части равенства (1) сущ. и явл. конечным числом, то н/с интеграл назыв. сходящимся, в противном случае – расходящимся

Б) н/с интеграл с бесконечным нижним пределом

О3. у= f(x) (-∞;b), которая определена и интегрируемана [А;В]с(-∞;b)

(2) 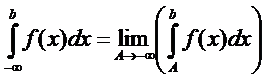--н/с интеграл с бесконечным нижним пр.

О4. понятие сходимости аналогично

В) н/с интеграл с двумя бесконечн. пределами интегр.

О5. у=f(x) (-∞;+∞), (А;В)с(-∞;+∞)

(3) --н/с интеграл с 2мя бесконечн пределами можно переписать как

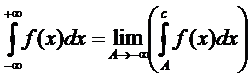
(4) 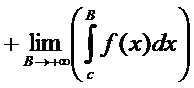где -∞<С<+∞ , (3)=(4)

И. на конечном промежутке

А)пусть ф-ция f(x) определена на конечном промежутке [a,b) и интегрируема на любом отрезке [a,x]Ì[a,b)

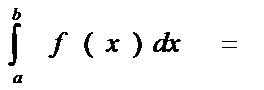
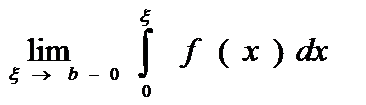
Иногда это выражение называют н/с и. второго рода.

Если конечн предел сущ., то и. 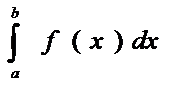наз. сходящимся, в противном случае – расходящимся.

Б)н/с интеграл от разрывных функции

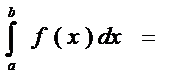
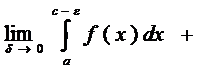
пусть задана ф-ция у=f(x) [a;b], причем cÎ[a;b], такая, что ф-ции f(x) в этой точке имеет бесконечный разрыв (x=c – точка разрыва второго рода) , тогда 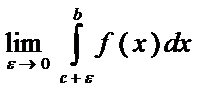--н/с интеграл от разрывной ф-ции

Если оба предела в правой части существуют и явл конечными числами, то н/с интеграл разрывн ф-ции назыв сходящимся, а если один из пределов не сущ. или =∞, то н/с интеграл наз. расходящимся

18. Несобственные интегралы от неограниченных ф-й.

Пусть ф-ция определена и интегрируема на замкнутом промежутке [a;b], за исключением конечного числа точек 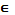[a;b], в которых ф-ция терпит разрыв 2-го рода. Тогда интеграл наз-ся несобственным интегралом от разрывной ф-ции и вычисляется по правилу:

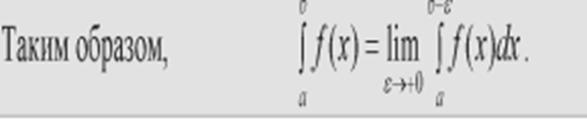
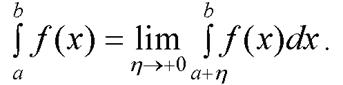
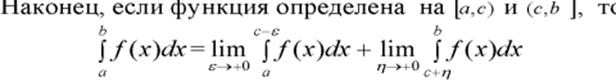
19. Дифференциальное уравнение(ДУ)

Осн.понятия

О1. ДУ – ур-е, сод неизв ф-цию, независ переем-ю и ее производные различных порядков.

Если неизв ф-ция зависит от одной независим переменной, то ДУ – обыкновенное ДУ (ОДУ).

Если неизв ф-ция содержит 2 и > независ переменных, то ДУ назыв ур-е частичных производных.

В общем виде ОДУ можно записать F(x,y,y’, … , y⁽ⁿ⁾)=0 (1) неявный

y⁽ⁿ⁾ =f(x,y,y’,…,y^(n-1)) (2)явный

Порядок старшей производной, входящей в ур-е назыв порядком ур-я.

О2. ф-ция у=у(х) наз решением ДУ (1) или (2) если, будучи подставленным в соответствующ ур-е вместе со всеми своими произв-ми, она обр-т его в верное рав-во. Задача нах-я решения ДУ наз задачей интегрирования ДУ.

О3. Общим решением ДУ (1), (2) n-го порядка назыв ф-ция вида y=j(x,c₁,c₂,…,c_n), которая зависит от переменной х и n произвольных постоянных

О4. Частичным реш ДУ наз реш, получ из общего при некот конкретных числовых значениях постоянных c₁,c₂,…,c_n

20. ДУ 1го порядка

Имеют вид: y’=f(x,y) (1) F(x,y,y’)=0 (2)

1) y’=f(x) dy/dx=f(x)

dy=f(x)dx òdy=òf(x)dx y=òf(x)dx

2) y’=f(y) dy/dx=f(y)

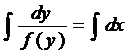
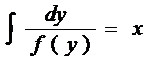
3) f(x)dx=f(y)dy ДУ с разделенными переменными òf(x)dx=òf(y)dy

4)y’=f(x)gy или M(x)N(y)d(x)=K(x)L(y)d(y)