Если ф-ция непрерывна в кажд. т. мн-ва Х, то она непрерывна в этой области

2. Частные производные первого и второго порядка

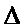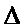Производная первого порядка(которая называется частной) Пусть х, у – приращения независимых переменных х и у в некоторой точке из области Х. Тогда величина, равная 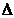z = f(x+ 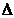х, y+ 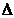у) = f(x,y) называется полным приращением в точке х_0,у_0.Если переменную х зафиксировать, а переменной у дать приращение 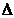у, то получим 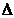zу = f(x,y,+ 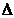у) – f(x,y). Аналогично определяется частная производная от переменной у, т.е.

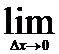
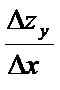
z’_x = 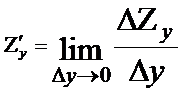Частную производную функции 2-х переменных находят по тем же правилам, что и для функций одной переменной.

Отличие состоит в том, что при дифференциации функции по переменной х , у считается const, а при дифференцировании по у, х считается const.

Для ф-и 2-х переем-х сущ 4 части произв-х 2 порядка: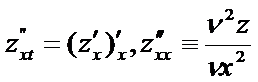

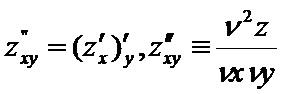
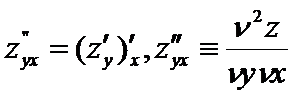
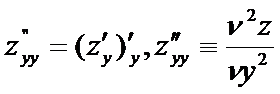
3. Полный дифференциал функции 2-х переменных

Пусть z = f(x,y), тогда dz = 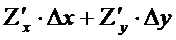- наз полным дифференциалом

Учитывая, что для ф-и f(x,y)=x, f(x,y)=y, df(x,y)=∆x=dx, df(x,y)=∆y=dy, полный диф-л можно записать в виде:

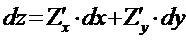Геометрич смысл. О. Т. 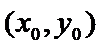наз max(min) ф-и z = f(x,y), если сущ некот окрест-ть т. 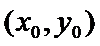такая, что для всех x,y из этой окрест-ти вып-ся нер-во f(x,y)<f 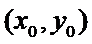(max) или f(x,y)>f 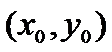(min). Т.: Если задана точка экс-ма ф-и 2-х переем-х , то знач-е частных произв-х в этой точке = 0, т.е. ,

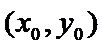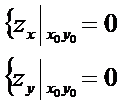
Точки 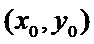, в которых частные производные первого порядка называются стационарными или критическими.

Поэтому для нахождения точек экстремума функции 2-х переменных используются достаточные условия экстремума.

Достат усл-е экстр-ма: Пусть функция z = f(x,y) дважды дифференцируема, и 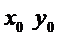стационарная точка,

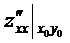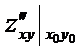A = , B = , C = 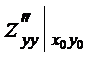, , 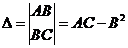тогда

1) 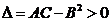, причем max, если A<0, min, если A>0.

2) 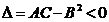, экстр-ма в т. нет

3) 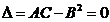, треб-ся доп исслед-е

приближ выч-ях знач-й ф-и 2-х переем-х, исп-ся след формула: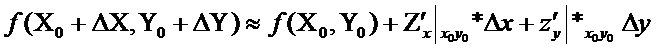

4.Экстремум функции двух переменных

Необходимые условия экстремума

О. Пусть функция z = f(x,y) определена в некоторой 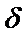- окрестности точки 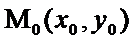. Тогда функция z = f(x,y) имеет в точке 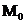максимум(минимум), если для всех точек этой окрестности выполняется неравенство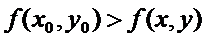

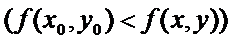
Т.(необходимое условие экстремума)

Пусть функция z = f(x,y) имеет экстремум в точке 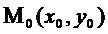. Тогда если в этой точке существуют конечные частные производные первого порядка, то они равны нулю.

Как и в случае функции одной переменной, точки, в которых все частные производные первого порядка равны нулю, называются критическими или точками, подозрительными на экстремум.

Заметим, что равенство нулю частных производных первого порядка – условие недостаточное. Действительно, рассмотрим, например, функцию z = xy. Частные производные 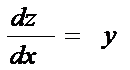и 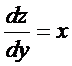равны 0 в точке (0,0), однако она не является точкой экстремума (так как в ее окружности функция z = xy может принимать и положительные значения).

Т.(достаточные условия экстремума) Пусть функция z = f(x,y) дважды дифференцируема, и 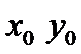стационарная точка,

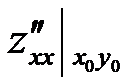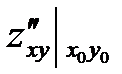A = , B = , C = 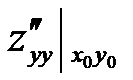, , 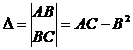тогда 1) 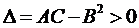, причем max, если A<0, min, если A>0. 2) 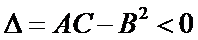, экстр-ма в т. 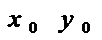нет 3) 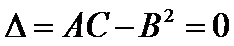, треб-ся доп исслед-е

5.М-д наим квадр-в. Выравн-е эмпирич данных по прямой

На практике часто приходится решать задачи сглаживанию эксперимент завис-тей.