Дифференцирование сложной функции.

Дифференцирование сложной функции.

Пусть функция имеет вид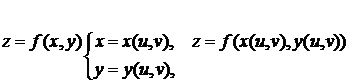

и пусть все 3 функции z, x и y дифференцируемы.

Т.к. функция z дифференцируема, то справедлива формула (1). Разделим ее почленно на 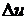, получим:

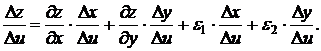
Положим 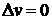, тогда получим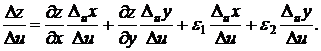

Устремим 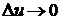, тогда получим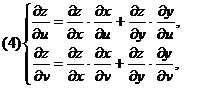

Пример.

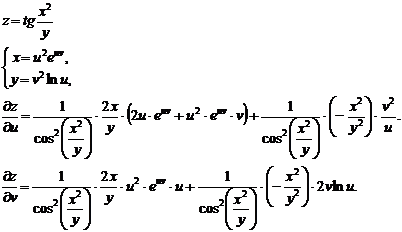
Полная производная.

Рассмотрим функцию 3-х переменных z=f(t,x,y), при этом 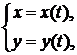т.е. z=f(t,x(t),y(t))=F(t).

Тогда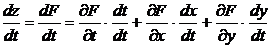

d означает производную функции одной переменной или полную производную.

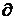означает частную производную, т.е. производную по одной из переменных.

Пример.

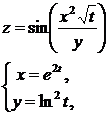
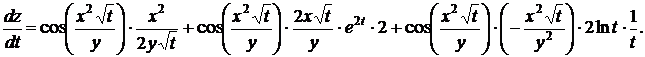
1. Дать определение неявной функции, сформулировать теорему ее существования и вывести формулы ее дифференцирования. Примеры.

Дифференцирование неявной функции.

Опр. Говорят, что соотношение F(x,y,z)=0 определяет неявную функцию 2-х переменных z=z(x,y), если при ее подстановке это соотношение обращается в тождество:

F(x,y,z(x,y))=0 (6)

Продифференцируем тождество 6 по переменной x, используя формулу полной производной, получим: 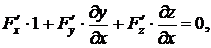где x и y независимые переменные, т.е. y не зависит от x, поэтому

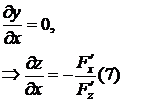
Аналогично,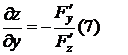

Если функция f(x,y,z) имеет 3 частные производные и 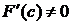в некоторой области, то частные производные неявной функции z находятся по формулам (7).

Пример. Найти частные производные неявной функции:

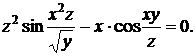
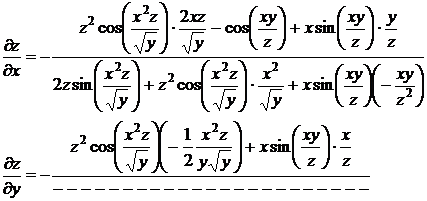
1. Рассказать об инвариантности формы 1-го дифференциала функции двух переменных. Высшие производные и дифференциалы. Примеры.

Инвариантность 1-ой формы дифференциала.

Пусть задана сложная функция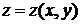

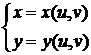
Предполагается, что все три функции дифференцируемы, тогда

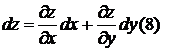
Т.к. функции x и y дифференцируемы, то

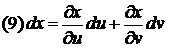
Аналогично

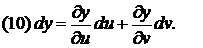
Подставим теперь (9) и (10) в (8) и получим:

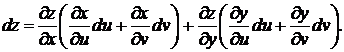
Перегруппируем

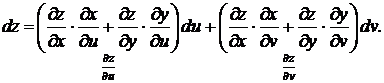
По формулам (4)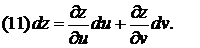

Свойство инвариантности формы 1-ого дифференциала заключается в следующем: вид дифференциала не изменяется в зависимости от того являются переменные промежуточными (x и y) или независимыми (u и v).

Замена переменной в неопределенном интеграле.

Опр.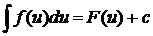

В качестве u может выступать дифференцируемая функция 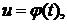тогда эта формула примет вид 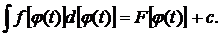(4)

Справедлива теорема:

Если функция 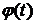дифференцируема и область ее значений попадает внутрь области определения функции f, а также во всей области 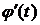сохраняет один и тот же знак, то справедлива формула (4).

Интегрирование по частям.

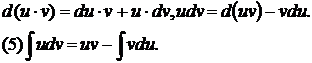
Эта формула применяется, когда функция u упрощается при дифференцировании, а именно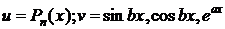

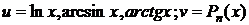и в некоторых других случаях.

1. Интегрирование 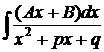и сопутствующих интегралов.

Интегрирование квадратного трехчлена.

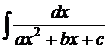Он вычисляется выделением в знаменателе полного квадрата и сводится таким образом к arctg или к высокому логарифму.

Похожими на эти интегралы являются следующие:

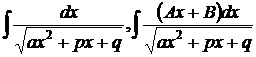Они сводятся к arcsin или к длинному логарифму.

1. Вывести формулу разложения многочлена на множители, используя основную теорему Безу. Интегрирование простейших рациональных дробей 4-х типов. Примеры.

Теорема Безу.

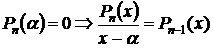
Доказательство.

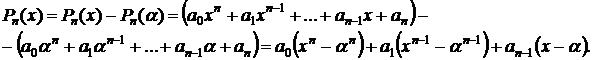
Каждое слагаемое полученного выражения делится на 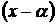, следовательно и все выражение делится на 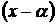.Теорема доказана.

Согласно основной теореме алгебры у нас имеется 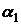, по теореме Безу:

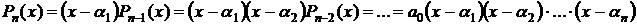Мы получили первичное разложение многочлена на простые множители. В этом разложении некоторые множители совпадают, а некоторые множители являются комплексными. Но так как коэффициенты уравнения вещественны, то комплексные множители всегда входят комплексно-сопряженными парами.

Задача о массе фигуры.

Пусть известна плотность фигуры в каждой точке 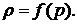Нам нужно найти массу фигуры. Задача решается для всех фигур одинаково.

1) Разобьем фигуру на n-частей, не обязательно равных.

2) В каждой из произвольной частей выберем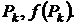

3) Будем считать плотность в этой точке, равной плотности всего кусочка.

Тогда масса кусочка 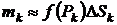(произведению плотности в этой точке на меру кусочка).

4) Складываем

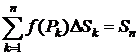
Полученное выражение называется n-ой интегральной суммой.

5) Перейдем к пределу

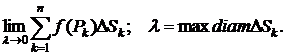
Полученный предел называется интегралом по фигуре и равен массе фигуры

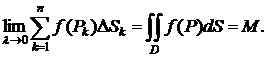
1. Дать определения интегральной суммы интеграла по фигуре для 5 типов фигур.

Интегральных сумм S_n бесконечно много. Здесь имеется 2 степени произвола: 1можно по разному разбивать фигуру на n-частей; 2можно по разному выбирать точку P_k каждой части.

1. Сформулировать условие существования интеграла по фигуре. Рассказать о механической интерпретации интеграла по фигуре и геометрической интерпретации опред. Двой. кривол.

Теорема. Если фигура ограничена, а подынтегральная функция непрерывна, то интеграл по фигуре существует.

На самом деле интеграл по фигуре существует и при гораздо меньших ограничениях, но нас вполне устраивают и эти.

Физически, если подынтегральная функция не отрицательна, то интеграл по фигуре можно трактовать, как массу этой фигуры, а подынтегральную функцию – как плотность этой фигуры.

Определенный интеграл.

Пусть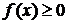

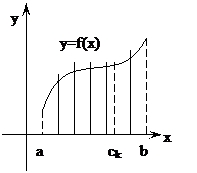
Полученная фигура называется криволинейной трапецией. Найдем ее площадь.

Разбиваем на n частей, не обязательно равных.

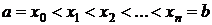
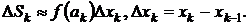
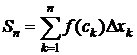- это и будет интегральная сумма.

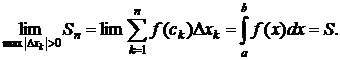
Итак, геометрически определенный интеграл – это площадь криволинейной трапеции.

Если у нас подынтегральная функция переменного знака, то берется алгебраическая сумма площадей.

Геометрический смысл двойного интеграла определяется совершенно аналогично, а именно

Геометрически двойной интеграл по области D от функции f(x,y) – это объем цилиндроида, основанием которого является область D, а верхней крышкой – подынтегральная функция f(x,y).

Геометрический смысл криволинейного интеграла по плоской кривой Г определяется аналогично..

Геометрический смысл криволинейного интеграла по плоской кривой 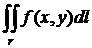- это площадь цилиндрической поверхности, направляющей которой является кривая 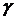, образующая параллельно оси OZ, а верхней крышкой является сечением подынтегральной функции.

Остальные типы интеграла по фигуре явного геометрического смысла не имеют.

1. Сформулировать и доказать основные свойства интеграла по фигуре (о немой переменной, линейность, аддитивность, значение интеграла при ).

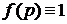Основные свойства определенного интеграла по фигуре.

В своем большинстве они одинаковы для всех 5 типов интегралов, следует однако отметить особую роль определенного интеграла, ибо к нему сводятся при вычислении все остальные типы интегралов, поэтому последние свойства будут сформулированы специально для определенного интеграла.

1) для определенного интеграла

В определенном интеграле переменная интегрирования немая.

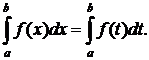
2)Аддитивность

относительно подынтегральной функции.

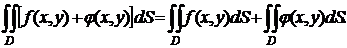
1) Однородность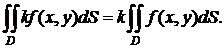

2) Аддитивность относительно области интегрирования.

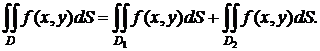
Физически это означает, что если пластинку разрезать на части, то ее масса равна сумме масс частей.

5)

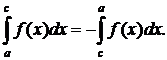
В определенном интеграле при перемене порядка интегрирования знак интеграла меняется на противоположный.

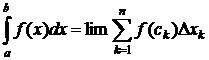
6) Это свойство лежит в основе геометрических и механических приложений интегралов по фигуре.

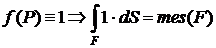
Ввиду важности этого свойства запишем его подробно для всех пяти типов фигур:

1.

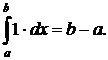
2.

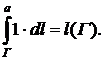
3.

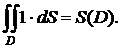
4.

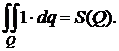
5.

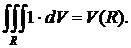
1. Сформулировать и доказать основные свойства интеграла по фигуре (интегрирование неравенств, теорема о среднем, теорема об оценке интеграла).

Интегрирование неравенств.

Если 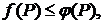то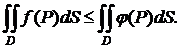

Замечание. Дифференцировать неравенство нельзя.

Формула прямоугольников.

Разбиваем область интегрирования на n-равных частей

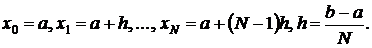
Затем заменяем площадь каждой маленькой криволинейной трапеции площадью прямоугольника.

Получаем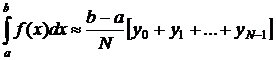

Можно записать эту же формулу, только брать в качестве высот правые концы, тогда

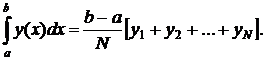
Эта формула не очень точна и годится для приближенной прикидки. Фактически здесь мы заменяем график подынтегральной функции некоторой ступенчатой кривой.

2) Формула трапеций.

Естественно, что если заменять график подынтегральной функции некоторой вписанной ломаной, то точность приближенной формулы повышается.

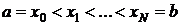
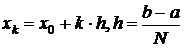
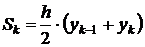
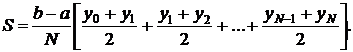
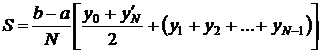
Число N выбирается произвольно. Чем больше N, тем выше точность вычисления. Если у нас задана точность 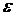, с которой нужно вычислить заданный интеграл, то можно поступать следующим образом.

Вычисляем интеграл дважды

Если 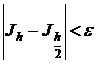, то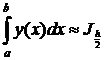

Если превышает, то мы снова увеличиваем в 2 раза число интервалов разбиений.

Наиболее точной из этих 3-х формул является формула парабол (формула Симпсона).

Ее идея состоит в замене двух соседних верхних крышек маленьких криволинейных трапеций куском параболы 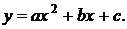Разобьем теперь 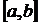на четное число частей.

Справедлива следующая лемма

Если криволинейная трапеция ограничена сверху параболой 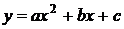, осью OX и двумя ординатами с расстояниями между ними 2h, то площадь этой трапеции

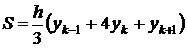
Доказательство.

Выберем систему координат следующим образом

Тогда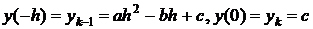

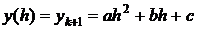
С другой стороны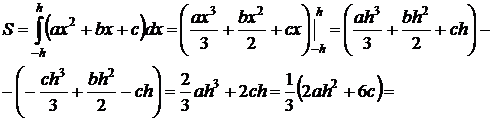

Попытаемся получить такое же выражение, не зная интегральных выражений y(-h), y(0), y(h).

Получим

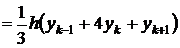
Лемма доказана.

Складывая площади всех маленьких трапеций получаем

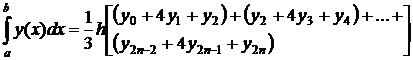
30. Дать определения и привести основные свойства несобственных интегралов с бесконечными пределами интегрирования. Примеры.

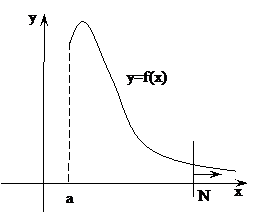
для линии y=f(x) ось OX является асимптотой.

.

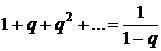Для вычисления этой площади нужно вычислить 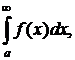его нельзя определить через интегральные суммы, как мы делали ранее, т.к. последний интервал всегда будет иметь бесконечную длину, поэтому мы поступим следующим образом:

Сначала обрежем бесконечный хвост, т.е. рассмотрим

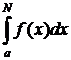- этот интеграл определяется обычно через предел интегральных сумм, а затем устремим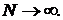

Если 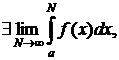то он и будет называться несобственным интегралом от функции f(x). Итак, процедура определения несобственного интеграла содержит 2 предельных перехода:

1. предел интегральных сумм;

2. предел определенного интеграла, когда его верхняя граница стремится к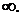

Если предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если этот предел не существует или равен бесконечности, то говорят, что несобственный интеграл расходится.

Несобственные интегралы с бесконечными пределами интегрирования от неотрицательных функций. Доказать признаки сравнения. Эталонные функции. Примеры.

Пусть подынтегральная функция 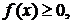тогда 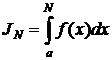является возрастающей функцией.

Таким образом у функции 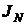имеется две возможности:

1) 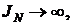т.е. возрастает неограниченно;

2) 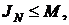т.е. ограничена сверху.

В этом случае по теореме о пределе монотонной переменной мы имеем, что существует предел 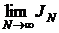и он не превосходит M, т.е.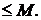

Т.е. в этом случае несобственный интеграл сходится.

Таким образом для неотрицательных функций исключается возможность отсутствия пределов у 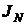. Это позволяет построить хорошую теорию исследования этих интегралов. Основной способ исследования на сходимость несобственных интегралов заключается в сравнении их с уже известными интегралами, иначе говоря с интегралами от так называемых эталонных функций.

Теорема 1. (признак сравнения в обычной форме).

Пусть функци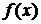и и 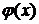не отрицательны интегрируемые и справедливо соотношение

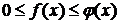для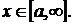

Тогда если 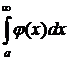сходится, то сходится 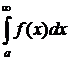. Если 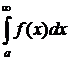расходится, то 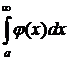тоже расходится.

Доказательство.

Проинтегрируем исходное неравенство в пределах от a до N, получим

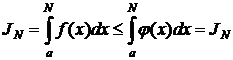
Если 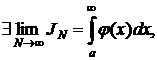то J_N ограничена сверху, 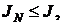а значит по теореме о пределе монотонной переменной 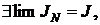т.е. интеграл сходится.

Обратное утверждение доказывается совершенно аналогично.

Гораздо чаще, чем теорема 1, на практике применяется теорема 2 (признак сравнения в предельной форме)

Пусть функци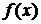и и 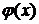неотрицательны и интегрируемые и пусть

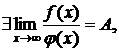при этом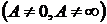

Тогда 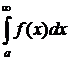и 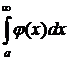сходятся и расходятся одновременно.

Доказательство.

По теореме о связи последовательности, имеющей предел с бесконечно малой, мы имеем 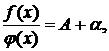где 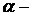БМ. Иначе говоря, для достаточно больших N справедливо соотношение

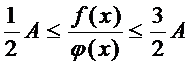
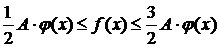
А теперь воспользуемся теоремой 1.

Для определения теорем сравнения нужно иметь набор эталонных функций, т.е. функции, о которых заранее известно сходятся или расходятся интегралы от них. В качестве таких функций чаще всего выбираются такие степенные функции

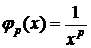
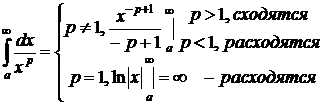
32.Дать определения абсолютной и условной сходимости несобственных интегралов. Доказать теорему о связи сходимости к абсолютной сходимости. Примеры.

Если подынтегральная функция имеет произвольный знак, то 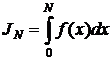- немонотонная функция и поэтому вся предыдущая теория не годится. Однако, имеется один частный, но важный случай, когда можно сказать что-то определенное и об этих интегралах. Это случай абсолютной сходимости.

Говорят, что 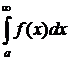сходится абсолютно, если сходится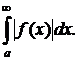

Теорема 3. Если интеграл сходится абсолютно, то он сходится.

Однако, возможна ситуация, когда интеграл от модуля расходится, а исходный интеграл сходится. В этом случае

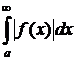- расходится; 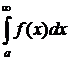- сходится условно.

Дать определение несобственных интегралов от неограниченных функций. Сформулировать их свойства, теоремы сравнения для них. Привести эталонные функции. Примеры.

Пусть функция f(x) определена на [a;b) и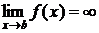

В этом случае опять нельзя определить интеграл обычным образом с помощью интегральных сумм, т.к. в последнем слагаемом 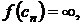поэтому опять обрезают хвост и определяем несобственный интеграл от неограниченной функции, как предел собственных интегралов при 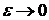, т.е.

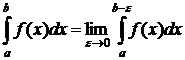
Если этот предел существует и конечен, то несобственный интеграл сходится. Если же он не существует или равен 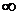, то несобственный интеграл расходится.

Все свойства несобственных интегралов 1-ого рода сохраняются и для несобственных интегралов 2-ого рода. Более того, если существует 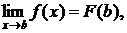то сохраняется и формула Ньютона-Лейбница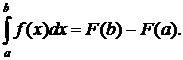

Замечание. Если точка разрыва 2-ого рода подынтегральной функции находится внутри области интегрирования, то мы вырезаем ее окрестность и получаем 2 несобственных интеграла 2-ого рода, при этом окрестности вырезаются вообще говоря не симметрично.

Для несобственных интегралов 2-ого рода от положительных функций также справедливы теоремы сравнения. Однако, в качестве эталонных функций выбираются функции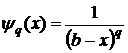

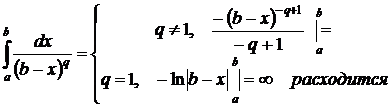
Рассказать о вычислении двойного интеграла в декартовых, полярных координатах и о перемене порядка интегрирования. Примеры.

Вычисление двойного интеграла сводится к вычислению 2-х определенных интегралов. Рассмотрим как это делается. Требуется вычислить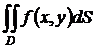

Область D называется правильной относительно оси OX, если всякая вертикальная прямая пересекает ее не более, чем в 2-х точках, называемых точками входа и выхода.

Аналогично, область называется правильной относительно оси OY, если всякая горизонтальная прямая пересекает эту область в 2-х точках.

Всякая неправильная область может быть разбита на конечное число правильных областей, поэтому будем считать, что область D – правильная.

Пусть сначала подынтегральная функция f(x,y) неотрицательна, тогда ее можно трактовать, как плотность функции 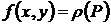и двойной интеграл представляет собой массу пластины.

Найдем сейчас эту массу другим способом: разобьем область D на вертикальные стержни, а затем каждый стержень на кусочки.

Элемент площади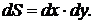

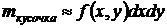
Масса стержня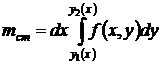

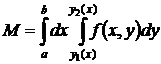
Итак, мы получили, что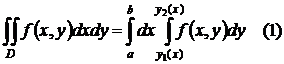

Эта формула справедлива и в тех случаях, когда функция f(x,y) имеет произвольный знак.

Дифференцирование сложной функции.

Пусть функция имеет вид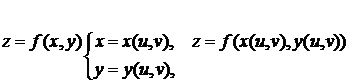

и пусть все 3 функции z, x и y дифференцируемы.

Т.к. функция z дифференцируема, то справедлива формула (1). Разделим ее почленно на 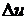, получим:

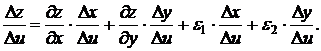
Положим 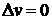, тогда получим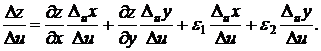

Устремим 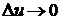, тогда получим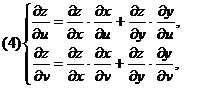

Пример.

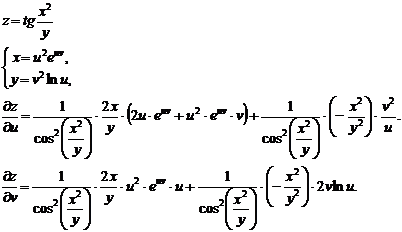
Полная производная.

Рассмотрим функцию 3-х переменных z=f(t,x,y), при этом 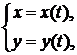т.е. z=f(t,x(t),y(t))=F(t).

Тогда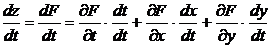

d означает производную функции одной переменной или полную производную.

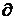означает частную производную, т.е. производную по одной из переменных.

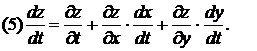
Пример.

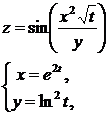
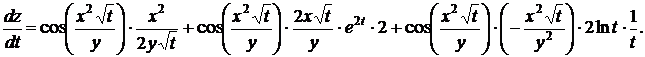
1. Дать определение неявной функции, сформулировать теорему ее существования и вывести формулы ее дифференцирования. Примеры.