П. 19.1. Вычисление тройного интеграла в декартовых координатах.

В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.

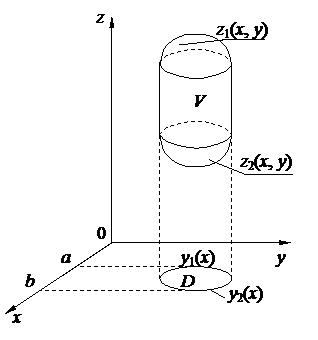Пусть область V ограничена снизу и сверху поверхностями z = z₁ (x, y) и z = z₂ (x, y) (z₁ (x, y) ≤ z₂ (x, y)). Тогда z₁ (x, y), z₂ (x, y) − определены и непрерывны на области D, которая является проекцией области V на плоскость Оху.

Будем считать область V правильной в направлении оси Oz, т. е. любая прямая параллельная оси Oz, пересекает границу области не более чем в двух точках.

Тогда для любой функции f (x, y, z) непрерывной в области V, имеет место формула

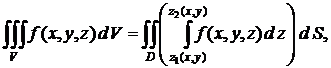
позволяющая свести вычисление тройного интеграла к последовательному вычислению внутреннего определенного интеграла по переменной z (при постоянных х и у) и внешнего двойного интеграла по области D. Результат вычисления внутреннего интеграла есть функция двух переменных х и у.

Если область D ограничена линиями х = а и х = b (a<b), y = y₁(x) и y = y₂(x), где у₁ и у₂ − непрерывные на [a, b] функции, причем у₁ (х) ≤ у₂ (х), то переходя от двойного интеграла по области D к повторному, получаем формулу

,

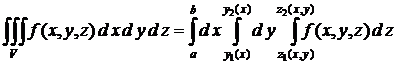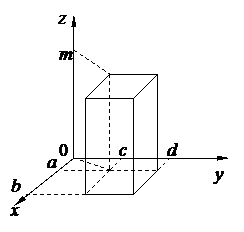сводящую вычисление тройного интеграла к последовательному вычислению трех определенных интегралов. Порядок интегрирования может быть и другим. В частности, если V − параллелепипед с гранями х = а и х = b (a<b), y = с и y = d, z = ℓ и z = m (ℓ < m), то

.

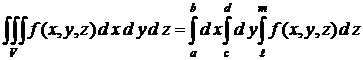В этом случае интегрирование можно проводить в любом порядке.

Пример 1. Вычислить 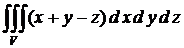, где V − параллелепипед, образованный плоскостями х = − 1; х = 1; у = 0; у = 1; z = 0; z = 2.

Решение. Подставим все известные значения в последнюю формулу и получим

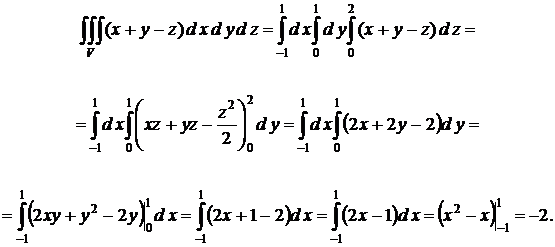
Пример 2. Вычислить 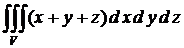, где V − параллелепипед, образованный плоскостями х + у + z = 1, х = 0; у = 0; z = 0.

Решение. Так как 0 ≤ z ≤ 1 − x − y, 0 ≤ y ≤ 1 − x, 0 ≤ x ≤ 1. Тогда

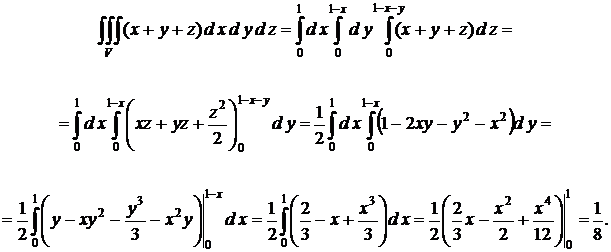
П. 19.2. Замена переменных в тройном интеграле.

Вычисление тройного интеграла в цилиндрических и

Сферических координатах.

Пусть требуется найти интеграл

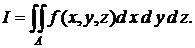
Предположим, что тело А, находящееся в пространстве xyz, связано взаимно однозначно с телом В, находящимся в пространстве uuv, при помощи формул

x = x (u, u, v), y = y (u, u, v), z = z (u, u, v). (1)

Будем предполагать, что у функций x (u, u, v), y (u, u, v), z (u, u, v) существуют непрерывные частные производные по u, u, v. Тогда формула замены переменных в тройном интеграле запишется в виде

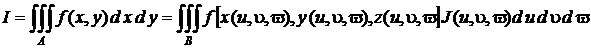, (2)

где u, u, v − криволинейные координаты точки (x, y, z), J (u, u, v) − абсолютная величина якобиана

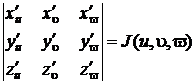
На практике часто встречаются два вида координат (x, y, z).

I. Цилиндрические координаты. Цилиндрическими координатами точки (x, y, z) называются числа r, j, z, где r и j − полярные координаты точки (x, y).

Ясно, что здесь

x = r cos j, y = r sin j, z = z

и потому якобиан этого преобразования

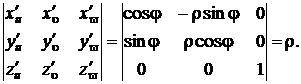
Стало быть, при переходе к цилиндрическим координатам общая формула (2) примет вид

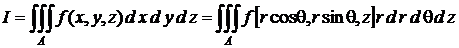. (3)

II. Сферические координаты. Сферическими координатам точки М(x,y, z) называются числа r, q, j, где q − угол между осью Оz и радиусом-вектором 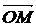точки М, r − длина этого радиус-вектора, т. е. расстояние между началом координат О и точкой М, а j − двугранный угол между полуплоскостью с ребром Oz, содержащей положительную часть оси Ох, и точку М. Из рисунка видно, что

OP = r sin q.

Так как х и у − проекции 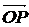на оси Ох и Оу, а z − проекция 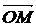на ось Oz, то

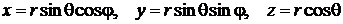. (4)

Полезно отметить также очевидное соотношение r² = x² + y² + z².

Соответствие, даваемое формулами (4), не взаимно однозначно. Чтобы получить все пространство xyz, достаточно изменять точку (r, q, j) в области, определяемой неравенствами

0 ≤ r < + ¥, 0 ≤ q ≤ p, 0 ≤ j ≤ 2p,

но и при этом ограничении мы добиваемся взаимной однозначности, так как плоскости r = 0 пространства rqj в пространстве xyz отвечает одна точка (0, 0, 0), а точками (r, 0, 0) и (r, q,2p) отвечает одна и та же точка (rsinq, 0, rcosq). Связанные с этими нарушениями взаимной однозначности осложнения не мешают, однако, применимости к нашему случаю общей формулы (2). Мы примем это без доказательства.

Якобиан в этом случае будет равен

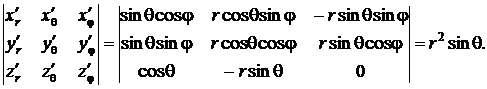
Тогда формула (2) примет вид

.(5)

Этой формулой удобно пользоваться тогда, когда f (x, y, z) имеет форму f (x² + y² + z²), а также когда областью А служит шар x² + y² + z² ≤ R² или какая-нибудь простая часть такого шара и т. п.

Пример. Найти

,

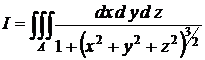если А − шар x² + y² + z² ≤ 1.

По формуле (5)

.

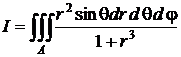Переходя к повторному интегралу, получаем

.

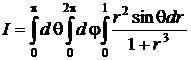Опуская простые пояснения, находим

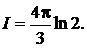
Криволинейные интегралы.

Определение. 1. Пусть в декартовых координатах x, y, z в каждой точке M (x, y, z) кривой L задан вектор F, т. е. задана векторная функция F (M) точек M Î L, и определен единичный вектор 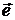(М) касательной к этой кривой.

Разобьем кривую L на п частей; Δℓ_i − длины отрезков разбиения (i = 1, 2, ¼, п). Внутри каждого отрезка разбиения произвольно возьмем точку М_i и вычислим в ней вектор F (M_i) и орт касательной 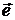(М_i). Вычислим скалярное произведение F (M_i) ∙ 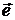(М_i) и составим сумму

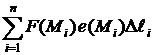(1)

которую назовем интегральной суммой векторной функции F (M) на кривой L.

Пусть l − длина наибольшего из элементов Δℓ_i.

Если существует предел интегральной суммы (1) при n ® ¥ и l ® 0, то этот предел называется криволинейным интегралом и обозначается

.

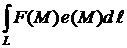Таким образом,

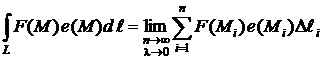. (2)

Определение 2. Так как скалярное произведение F (M) e (M) = f (M) − скалярная функция точек М кривой L, то равенство (2) может быть преобразовано в равенство

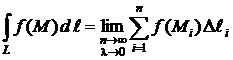, (3)

левая часть которого называется криволинейным интегралом I − рода (или криволинейным интегралом по длине дуги кривой).

Определение 3. В декартовом базисе i, j, k, ассоциированном с принятой здесь системой декартовых координат, векторная функция F (M) и орт касательной e (M) задаются в виде

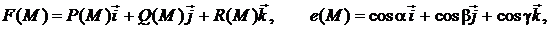
где P (M), Q (M), R (M) − скалярные функции точке М кривой L; a, b, g − углы, образуемые касательной к L в точках M Î L с осями координат x, y, z соответственно. Скалярное произведение этих векторов

F (M)∙e (M) = P (M)∙cos a + Q (M)∙cos b + R (M)∙cos g. (4)

Пусть Δx, Δy, Δz − проекции отрезка Δℓ на координатные оси. Тогда

Δx = Δℓ∙cos a, Δy = Δℓ∙cos b, Δz = Δℓ∙cos g. (5)

Равенства (4), (5) позволяют записать

F (M)∙e (M)∙Δℓ = P (M)∙Δх + Q (M)∙Δу + R (M)∙Δz. (6)

С учетом этого равенство (2) преобразуется к виду

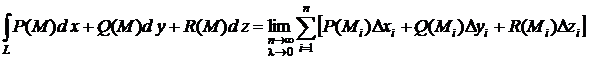. (7)

Левая часть этого равенства называется криволинейным интегралом второго рода (или криволинейным интегралом по координатам).

Обратим внимание, что все три типа криволинейных интегралов (2), (3), (7) связаны друг с другом.