РАЗДЕЛ 10. Кратные интегралы.
РАЗДЕЛ 10. Кратные интегралы.
НАЧАЛЬНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Def. Пусть 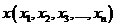 ,
, 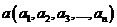 ,
, 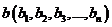
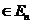 .
.
Множество 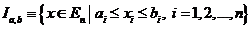 называется замкнутым промежутком или замкнутым брусом в
называется замкнутым промежутком или замкнутым брусом в 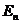 .
.
Множество 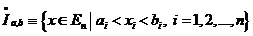 называется открытым промежутком
называется открытым промежутком
или открытым брусом в 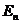 .
.
Def. Мерой промежутков 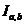 и
и 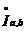 называется величина:
называется величина:
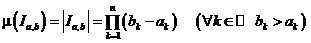 ( Точнее
( Точнее 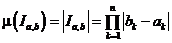 ).
).
Def. Если 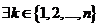 такое, что
такое, что 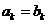 то промежуток
то промежуток 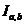 называется вырожденным и
называется вырожденным и 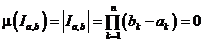 .
.
Свойства меры промежутка:
а). Положительность: 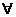
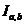
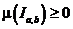 , причем
, причем 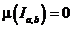 тогда и только тогда, когда
тогда и только тогда, когда 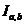 – вырожден.
– вырожден.
б). Положительная однородность: 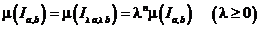 .
.
в). Аддитивность:
* для 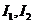 таких, что
таких, что 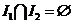 Þ
Þ 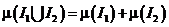 ;
;
* для 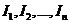 и
и 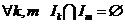 Þ
Þ 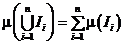 .
.
г). Монотонность меры: 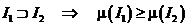 .
.
Def. Диаметром бруса (промежутка) называется величина:
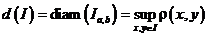
Отметим, что 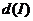 и
и 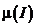 – это не одно и тоже. Например, если
– это не одно и тоже. Например, если 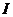 – вырожден, то
– вырожден, то 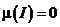 , a
, a 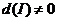 (вообще говоря).
(вообще говоря).
При этом: * 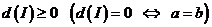 ;
;
* 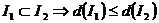 ; *
; * 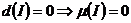 .
.
Def. Совокупность 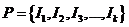 подпромежутков промежутка
подпромежутков промежутка 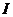 называется разбиением промежутка
называется разбиением промежутка 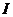 , если: *
, если: * 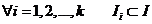 ;
;
* 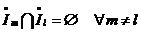 ; *
; * 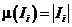 ; *
; * 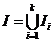 ; *
; * 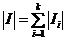 .
.
Величина 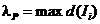 называется параметром разбиения P (при этом
называется параметром разбиения P (при этом 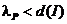 ).
).
Def. Разбиение 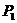 называется измельчением разбиения
называется измельчением разбиения 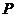 , если все элементы разбиения
, если все элементы разбиения 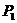 получены разбиением элементов разбиения
получены разбиением элементов разбиения 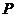 .
.
Обозначается: 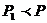 . Читается:
. Читается: 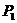 мельче
мельче 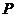 или
или 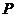 крупнее
крупнее 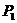 .
.
Для отношения “ крупнее – мельче” справедливо:
*. транзитивность – 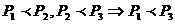 ; *.
; *. 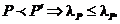 ;
;
*. 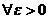
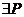
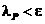 ; *.
; *. 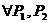
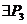 |
| 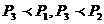 .
.
Определение кратного интеграла
Пусть 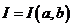 – брус (промежуток) в
– брус (промежуток) в 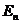 ,
, 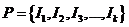 – разбиение промежутка I. На каждом из промежутков разбиения
– разбиение промежутка I. На каждом из промежутков разбиения 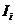 отметим точку
отметим точку 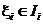 .
.
Получим 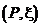 разбиение с отмеченными точками для
разбиение с отмеченными точками для 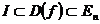 .
.
Величина 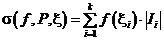 называется интегральной суммой Римана для функции f (x) на промежутке I по разбиению с отмеченными точками
называется интегральной суммой Римана для функции f (x) на промежутке I по разбиению с отмеченными точками 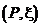 .
.
Def: 
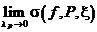 =
= 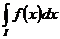 =
= 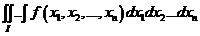 .
.
Обозначая 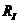 – множество функций интегрируемых на брусе I запишем:
– множество функций интегрируемых на брусе I запишем:
Def: 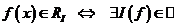
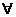 ε > 0
ε > 0 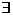 δ > 0
δ > 0 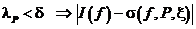 <
< 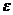 .
.
Если для функции f (x) на I и разбиения 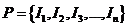 – обозначить через
– обозначить через 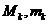 – наибольшее и наименьшее значение функции f (x) на Ik то величины
– наибольшее и наименьшее значение функции f (x) на Ik то величины 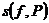 =
= 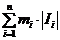 и
и 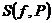 =
= 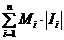 называются нижней и верхней суммами Дарбу.
называются нижней и верхней суммами Дарбу.
§. Критерий Дарбу существования кратного интеграла.
Т0. Чтобы функция 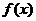 была интегрируема на брусе
была интегрируема на брусе 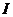 (т.е.
(т.е. 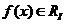 ) необходимо и достаточно, чтобы
) необходимо и достаточно, чтобы 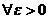
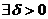
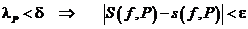 . Δ▲.
. Δ▲.
Определено интегрирование функции по брусу в евклидовом пространстве. А как функцию проинтегрировать по произвольному ограниченному множеству из евклидового пространства?
Определим интеграл от функции f по множеству 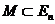 .
.
Def: Пусть 
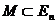 и
и 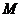 – ограничено, т.е.
– ограничено, т.е. 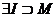 . Функцию
. Функцию 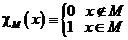 назовём характеристической функцией множества M .
назовём характеристической функцией множества M .
Тогда: 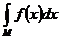 ≡
≡ 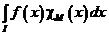 .
.
Определение интеграла по множеству не зависит от того, какой брус, содержащий М выбран, т.е. 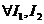
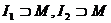
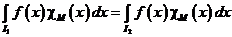 .
.
Это обозначает, что определение интеграла по множеству корректно.
Необходимое условие интегрируемости.Чтобы функция f (x) на М была интегрируемой необходимо, чтобы f (x) была ограниченной на М. Δ▲.
От пути интегрирования.
Т0. Пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) определены и непрерывны в
области G , лежащей на гладкой поверхности S, и γ – граница области G.
Тогда эквивалентны следующие условия:
A*). Для любого замкнутого контура γ в G 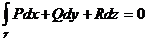 ;
;
B*). Для любых A,B є G 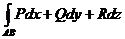 не зависит от кривой, соединяющей
не зависит от кривой, соединяющей
точки A и B, и лежащей в области G;
С*). Выражение Pdx + Qdy + Rdz в G является полным дифференциалом
некоторой функции U(x, y, z), т.е. 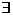 U = U(x, y, z) такая,что dU = Pdx+Qdy+Rdz;
U = U(x, y, z) такая,что dU = Pdx+Qdy+Rdz;
D*). Для функций P(x, y, z), Q(x, y, z), R(x, y, z) в области G выполняются условия:
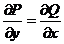 ;
; 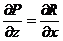 ;
; 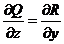 .
.
При этом : 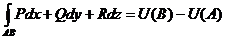 (*)
(*)
Последнюю формулу можно назвать формулой Ньютона-Лейбница для криволинейных интегралов.
Замечание 1. (связь А* и В*). 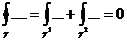
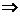
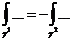
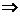
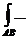 не зависит от кривой L, соединяющей точки А и В.
не зависит от кривой L, соединяющей точки А и В.
Замечание 2. (связь С* и D*).
Если 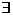 U(x, y, z) такая, что
U(x, y, z) такая, что 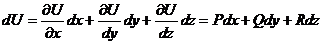 ,
,
то 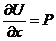 ,
, 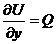 Þ
Þ 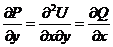 ;
;
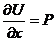
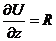 Þ
Þ 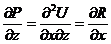 ;
; 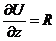
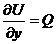 Þ
Þ 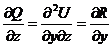 .
.
Замечание 3. В случае независимости криволинейного интеграла от пути
интегрирования, 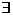 U(x, y, z) такая что:
U(x, y, z) такая что:
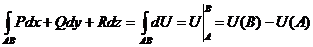 .
.
Физикиназывают функцию U(x, y, z) потенциалом векторного поля 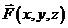 , а поле F – потенциальным – “ Работа равна разности потенциалов”.
, а поле F – потенциальным – “ Работа равна разности потенциалов”.
Математики называют функцию U(x, y, z) первообразной для Pdx+Qdy+Rdz –
интеграл равен разности первообразных в конце и начале пути.
Примеры:
 10.Вычислить
10.Вычислить 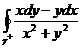 для различных контуров γ.
для различных контуров γ.
а). Пусть контур γ ограничивающий область G таков, что 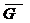 не содержит т. (0,0). Для вычисления интеграла воспользуемся формулой Грина.
не содержит т. (0,0). Для вычисления интеграла воспользуемся формулой Грина.
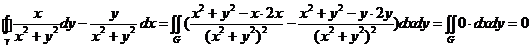 где,
где,
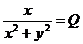 ,
, 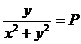 ,
, 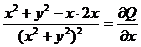 ,
, 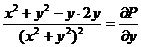 .
.
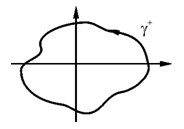
б). Пусть контур γ+ окружает точку (0,0). В этом случае нельзя применить формулу Грина ибо 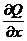 и
и 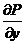 в точке (0,0) не существуют.
в точке (0,0) не существуют.
Отметим, что все интегралы по таким контурам совпадают между собой.
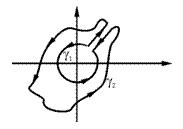 Иллюстрация :
Иллюстрация : 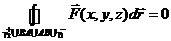 Þ
Þ
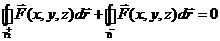 Þ
Þ 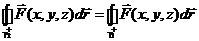 .
.
в). Тогда достаточно вычислить 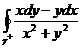 скажем, по окружности
скажем, по окружности 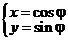 .
. 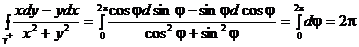 .
.
г). Легко видеть, что 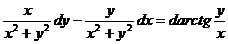 .
.
Следовательно, 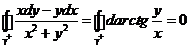 , если контур не проходит через точку (0,0) т.к. начальная и конечная точки замкнутого контура совпадают.
, если контур не проходит через точку (0,0) т.к. начальная и конечная точки замкнутого контура совпадают.
20. Найти первообразную, если:
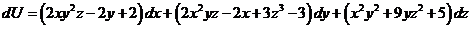 .
.
Проверка показывает, что условия 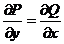 ;
; 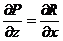 ;
; 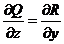 выполняются.
выполняются.
Таким образом, задача о нахождении первообразной поставлена корректно. Тогда,
1). 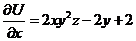 и интегрирование по
и интегрирование по 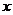 дает:
дает: 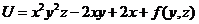 .
.
Отсюда 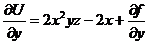 . Но
. Но 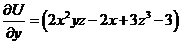 из условия задачи.
из условия задачи.
2). Тогда 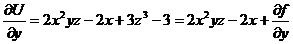 Þ
Þ 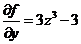 .
.
Интегрирование по 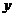 дает
дает 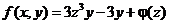 .
.
Значит: 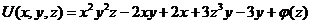 .
.
Отсюда 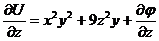 . Но из условия задачи
. Но из условия задачи 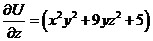 .
.
3) Тогда 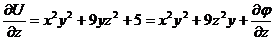 Þ
Þ 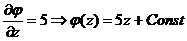 .
.
Итог: 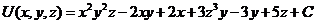 . Первообразная найдена с точностью до произвольного постоянного слагаемого. Большего и желать не приходится.
. Первообразная найдена с точностью до произвольного постоянного слагаемого. Большего и желать не приходится.
0
Пусть вЕ3 задана поверхность 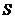 :
: 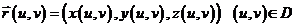 ;
;
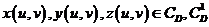 , и на поверхности S задана вектор-функция
, и на поверхности S задана вектор-функция
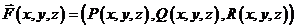
и, при этом 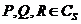 .
.
Рассмотрим: 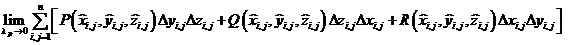 .
.
Если такой предел существует и конечен, то он называется поверхностным интегралом 2-го рода и обозначается 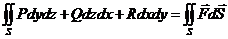 .
.
Физический смыслповерхностного интеграла 2-го рода – поток векторного поля 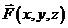 через поверхность S в направлении нормали, определяемой вектором
через поверхность S в направлении нормали, определяемой вектором 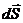 , т.е. стороной поверхности. Собственно говоря, это и есть определение потока векторного поля через поверхность.
, т.е. стороной поверхности. Собственно говоря, это и есть определение потока векторного поля через поверхность.
Свойстваповерхностного интеграла 2-го рода:
1°. Интеграл меняет знак при изменении стороны поверхности, по которой идет интегрирование: 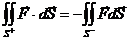 .
.
2°. Связь с поверхностным интегралом 1 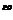 рода.
рода.
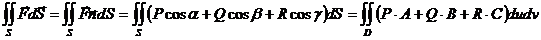 .
.
Здесь 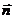 единичный вектор нормали к поверхности;
единичный вектор нормали к поверхности; 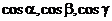 – направляющие косинусы нормали к поверхности;
– направляющие косинусы нормали к поверхности; 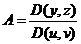 ,
, 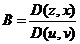 ,
, 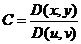 ;
;
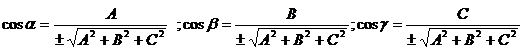 .
.
3°. Если помнить о том, что: 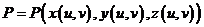 ,
,
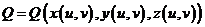 ,
, 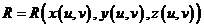 , легко написать формулу для вычисления поверхностного интеграла 2-го рода
, легко написать формулу для вычисления поверхностного интеграла 2-го рода
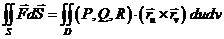 .
.
Примеры вычисления поверхностных интегралов 2  рода.
рода.
1°. Вычислить 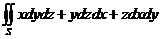 , где S – внешняя сторона сферы
, где S – внешняя сторона сферы 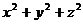 =
= 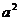
Вектор нормали 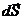 был найден в предыдущем параграфе, в примере 3°.
был найден в предыдущем параграфе, в примере 3°.
 .
.
Знак в выражении для 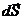 берем так, чтобы в 1
берем так, чтобы в 1 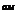 октанте координаты вектора
октанте координаты вектора 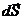 были положительными (внешняя сторона).
были положительными (внешняя сторона).
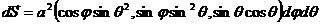 .
.
Вектор  .
.
Тогда: 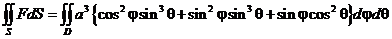 =
=
= 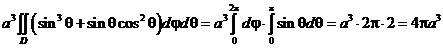 . ▲
. ▲
2°. Вычислить 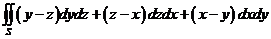 , если S- внешняя сторона конуса
, если S- внешняя сторона конуса
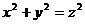 с крышкой z = 1.
с крышкой z = 1.
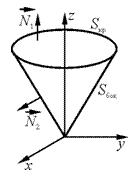 Δ Поверхность интегрирования состоит из двух частей – боковой поверхности конуса и крышки. Поэтому:
Δ Поверхность интегрирования состоит из двух частей – боковой поверхности конуса и крышки. Поэтому: 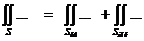 .
.
а). Для вычисления первого из них, отметим что 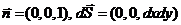 и, следовательно:
и, следовательно:
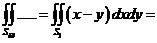
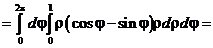
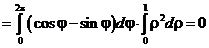 .
.
б). Для вычисления второго из них, вспомним что для поверхности, заданной явно: 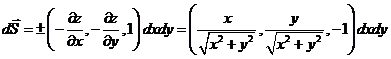 . Знак выбран так, чтобы получить внешнюю нормаль к поверхности. Получаем:
. Знак выбран так, чтобы получить внешнюю нормаль к поверхности. Получаем:
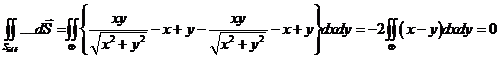 .
.
Таким образом 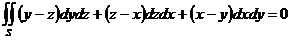 .
.
Скалярные поля.
 Пусть задана область
Пусть задана область 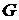 в евклидовом пространстве
в евклидовом пространстве 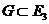 и в
и в 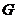 задана функция
задана функция 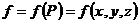 . Тогда говорят, что в
. Тогда говорят, что в 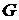 задано скалярное поле (синоним: функция трех переменных). Поверхности
задано скалярное поле (синоним: функция трех переменных). Поверхности 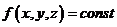 называются поверхностями уровня скалярного поля.
называются поверхностями уровня скалярного поля.
Пусть задан вектор с известными направляющими косинусами 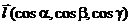 .
.
Производной скалярного поля по направлению 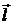 называется величина:
называется величина:
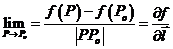 .
.
Запишем параметрическое уравнение прямой 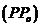 :
:
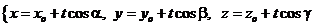 ;
;
Тогда на этой прямой:
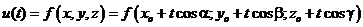 и тогда:
и тогда:
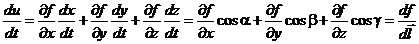 .
.
Вводя вектор 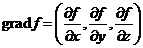 получим:
получим: 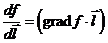 .
.
Из  делаем вывод, что вектор
делаем вывод, что вектор 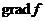 указывает направление максимального роста поля и по величине равен скорости роста поля в этом направлении.
указывает направление максимального роста поля и по величине равен скорости роста поля в этом направлении.
Такое определение 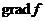 является инвариантным относительно системы координат.
является инвариантным относительно системы координат.
Если для векторного поля 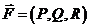 существует скалярное поле
существует скалярное поле 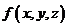 такое, что
такое, что 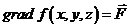 то поле
то поле 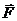 называется потенциальным полем а скалярное поле
называется потенциальным полем а скалярное поле 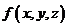 называется его потенциалом.
называется его потенциалом.
Необходимое и достаточное условие потенциальности поля 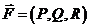 :
:
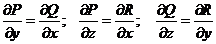 .
.
Векторные поля.
Пусть задана область 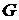 в евклидовом пространстве
в евклидовом пространстве 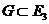 , и в
, и в 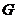 задана векторная функция
задана векторная функция 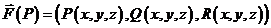 . Тогда, говорят что в
. Тогда, говорят что в 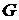 задано векторное поле.
задано векторное поле.
Def: Линии в пространстве в каждой точке которых векторное поле направлено по касательной к данной линии называется векторными линиями поля (силовыми линиями, линиями тока).
Векторные линии можно найти исходя из системы дифференциальных уравнений векторных линий: 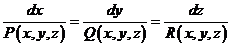
 , например для
, например для 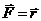 :
: 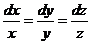 Þ
Þ 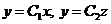 – прямые, проходящие через начало координат.
– прямые, проходящие через начало координат.
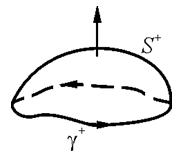
Теорема Стокса.
Пусть в 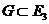 заданы функции
заданы функции 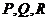 , непрерывные вместе со своими первыми производными
, непрерывные вместе со своими первыми производными 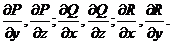 Пусть
Пусть 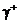 замкнутый контур в
замкнутый контур в 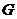 , а
, а 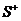 –поверхность в
–поверхность в 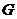 натянутая на контур
натянутая на контур 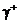 , причем
, причем 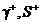 одинаково взаимно ориентированы. Тогда:
одинаково взаимно ориентированы. Тогда:
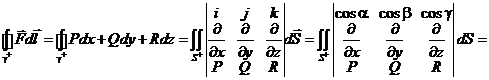
= 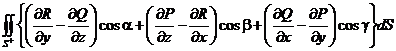 =
=
= 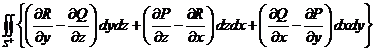 .
.
∆. Интеграл 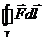 по замкнутому контуру называется циркуляцией векторного поля.
по замкнутому контуру называется циркуляцией векторного поля.
а). Пусть 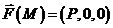 .
.
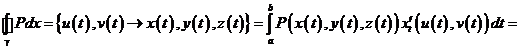
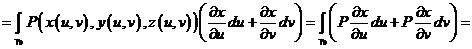
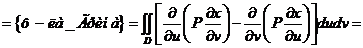
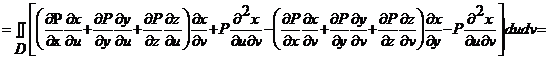
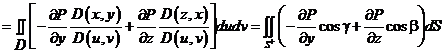
б), в) Аналогично:
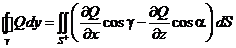 ,
, 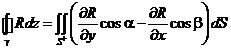 .
.
Суммируя полученные три формулы, получаем формулу Стокса. ▲.
 Def: Вектор с координатами
Def: Вектор с координатами 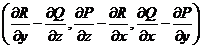 называется ротором векторного поля
называется ротором векторного поля 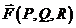 .
. 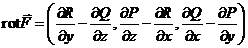 ,
,
и тогда формула Стокса запишется так: 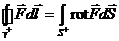 .
.
Рассмотрим 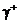 ,
, 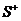 и
и 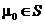 , найдем:
, найдем:
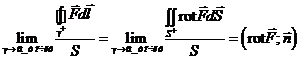 следовательно:
следовательно: 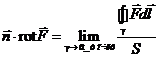
Получили инвариантное относительно системы координат определение 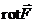 :
:
Проекция ротора векторного поля 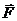 на вектор нормали к поверхности определяется пределом отношения циркуляции
на вектор нормали к поверхности определяется пределом отношения циркуляции 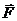 вдоль замкнутого контура к мере поверхности ограниченной данным контуром, когда контур стягивается в точку. И теорема Стокса:
вдоль замкнутого контура к мере поверхности ограниченной данным контуром, когда контур стягивается в точку. И теорема Стокса:
Циркуляция векторного поля 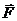 вдоль контура
вдоль контура 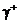 есть сумма циркуляций поля
есть сумма циркуляций поля 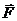 в точках расположенных на поверхности
в точках расположенных на поверхности 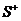 , краем которой является контур
, краем которой является контур 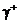 .
.
РАЗДЕЛ 10. Кратные интегралы.
НАЧАЛЬНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Def. Пусть 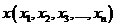 ,
, 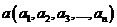 ,
, 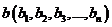
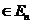 .
.
Множество 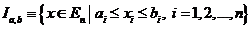 называется замкнутым промежутком или замкнутым брусом в
называется замкнутым промежутком или замкнутым брусом в 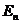 .
.
Множество 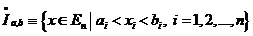 называется открытым промежутком
называется открытым промежутком
или открытым брусом в 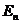 .
.
Def. Мерой промежутков 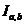 и
и 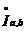 называется величина:
называется величина:
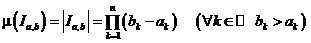 ( Точнее
( Точнее 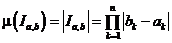 ).
).
Def. Если 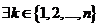 такое, что
такое, что 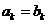 то промежуток
то промежуток 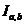 называется вырожденным и
называется вырожденным и 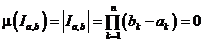 .
.
Свойства меры промежутка:
а). Положительность: 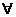
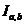
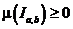 , причем
, причем 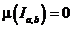 тогда и только тогда, когда
тогда и только тогда, когда 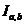 – вырожден.
– вырожден.
б). Положительная однородность: 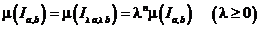 .
.
в). Аддитивность:
* для 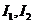 таких, что
таких, что 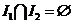 Þ
Þ 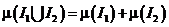 ;
;
* для 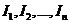 и
и 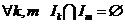 Þ
Þ 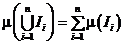 .
.
г). Монотонность меры: 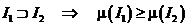 .
.
Def. Диаметром бруса (промежутка) называется величина:
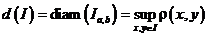
Отметим, что 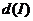 и
и 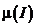 – это не одно и тоже. Например, если
– это не одно и тоже. Например, если 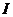 – вырожден, то
– вырожден, то 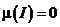 , a
, a 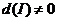 (вообще говоря).
(вообще говоря).
При этом: * 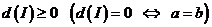 ;
;
* 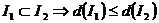 ; *
; * 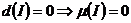 .
.
Def. Совокупность 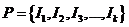 подпромежутков промежутка
подпромежутков промежутка 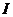 называется разбиением промежутка
называется разбиением промежутка 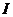 , если: *
, если: * 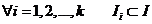 ;
;
* 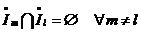 ; *
; * 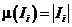 ; *
; * 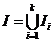 ; *
; * 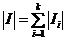 .
.
Величина 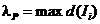 называется параметром разбиения P (при этом
называется параметром разбиения P (при этом 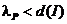 ).
).
Def. Разбиение 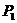 называется измельчением разбиения
называется измельчением разбиения 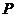 , если все элементы разбиения
, если все элементы разбиения 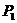 получены разбиением элементов разбиения
получены разбиением элементов разбиения 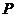 .
.
Обозначается: 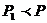 . Читается:
. Читается: 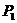 мельче
мельче 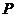 или
или 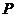 крупнее
крупнее 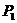 .
.
Для отношения “ крупнее – мельче” справедливо:
*. транзитивность – 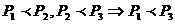 ; *.
; *. 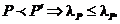 ;
;
*. 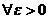
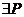
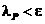 ; *.
; *. 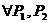
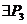 |
| 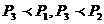 .
.
