Раздел VI. Физика атома. Физика твердого тела.

Физика атомного ядра и элементарных частиц

Строение атома. Теория Бора. Опыты Резерфорда по рассеиванию α- частиц. Модель атома по Резерфорду. Следствия из модели Резерфорда. Спектры излучения атомов и их количественное описание. Модель атома Бора. Постулаты Бора. Теория водородоподобного атома Бора. Опыт Франка и Герца.

Элементы квантовой механики. Гипотеза де Бройля. Опыты Девиссона и Джермера. Формула де Бройля для свободной частицы. Границы применимости классической механики. Соотношение неопределенностей. Применение соотношения неопределенностей к решению квантово-механических задач. Уравнение Шредингера для стационарных состояний. Решение уравнения Шредингера для случая частицы в бесконечно глубокой «потенциальной яме». Энергетический спектр частицы в «потенциальной яме». Уравнение Шредингера для атома водорода.

Спин электрона. Магнитные свойства атома. Тонкая структура спектров щелочных металлов. Опыты Штерна и Герлаха. Понятие о спине электрона. Полный момент импульса электрона в атоме. Полный магнитный момент атома. Эффект Зеемана. Принцип Паули. Распределение электронов в атоме.

Элементы квантовой теории кристаллов. Анизотропия кристаллов. Моно- и поликристаллы. Кристаллическая решетка. Виды межатомных связей в кристаллических телах. Квантовая теория теплоемкости Дебая. Фотоны.

Электронный газ. Энергетические зоны кристаллической решетки. Вырождение электронного газа. Функция Ферми. Энергия Ферми.

Диэлектрики и металлы. Изоляторы, проводники и полупроводники. Свойства диэлектриков с точки зрения зонной теории. Квантовая теория электропроводности, теплопроводности, контактных явлений. Сверхпроводимость – макроскопический квантовый эффект. Магнитные свойства металлов. Спиновая природа ферромагнетизма. Доменная структура ферромагнетиков. Анализ кривой намагничивания.

Полупроводники. Основные особенности структуры энергетических зон в полупроводниках. Собственная электронная и дырочная проводимость.

Доноры и акцепторы. Примесная проводимость. Явления на границе полупроводника с металлом. Контакт двух полупроводников различных типов (p-; n- переходы). Полупроводниковые диоды и триоды. Действие света на полупроводники.

Строение и свойства атомных ядер. Состав ядра: протоны и нейтроны. Основные характеристики нуклонов и ядер. Изотопы. Понятие о ядерных силах. Масса и энергия связи в ядре. Средняя энергия нуклонов и ее зависимость от массового числа. Неустойчивость тяжелых ядер по отношению к некоторым типам распада.

Радиоактивность. Ядерные реакции. Сущность явлений радиоактивности. Закон радиоактивного распада. Период полураспада. Типы радиоактивного распада. Основные характеристики α-распада, β-распада. Спектр β-частиц. Нейтрино. Гамма-излучения радиоактивных ядер. Понятие о ядерных реакциях. Законы сохранения в ядерных реакциях. Деление тяжелых ядер. Понятие об элементарных частицах.

КОНТРОЛЬНАЯ РАБОТА № 3 3

РАЗДЕЛ IV. ЭЛЕКТРОМАГНЕТИЗМ

Основные формулы

1. Связь магнитной индукции 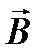с напряженностью 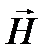магнитного поля:

,

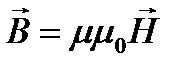где 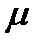−магнитная проницаемость изотропной среды; 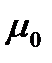− магнитная постоянная ( 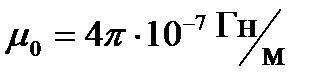). В вакууме µ = 1, и тогда магнитная индукция в вакууме:

.

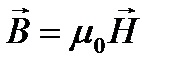2. Закон Био-Савара-Лапласа:

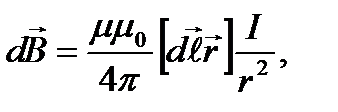или ,

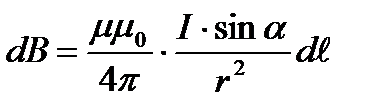где 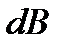− магнитная индукция поля, создаваемого элементом проводника длиной 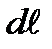с током 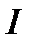; 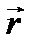− радиус-вектор, направленный от элемента-проводника к точке, в которой магнитная индукция вычисляется; 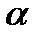− угол между радиусом-вектором и направлением тока в элементе проводника.

3. Магнитная индукция в центре кругового тока:

,

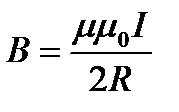где R – радиус кругового витка.

4. Магнитная индукция на оси кругового тока:

,

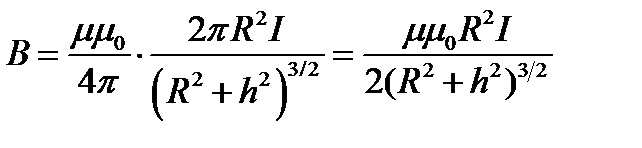где h – расстояние от центра витка до точки, в которой вычисляется магнитная индукция.

5. Магнитная индукция поля прямого тока:

,

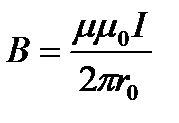где r₀ – расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.

6. Магнитная индукция поля, создаваемого отрезком провода с током (рисунок, а):

.

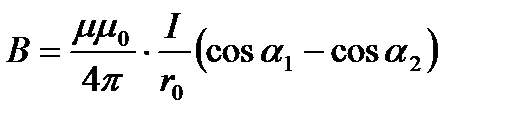Обозначения ясны из рисунка. Направление вектора магнитной индукции 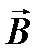обозначено точкой – это значит, что 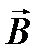направлен перпендикулярно плоскости чертежа к нам.

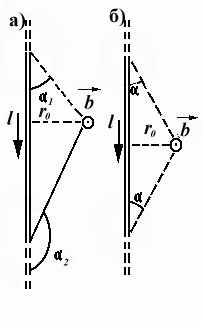
7. Магнитная индукция поля соленоида:

,

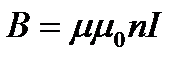где п – число витков соленоида, приходящееся на единицу длины.

8. Сила, действующая на проводник с током в магнитном поле, закон Ампера:

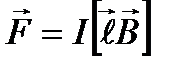, или ,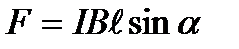

где 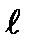− длина проводника; 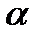− угол между направлением тока в проводнике и вектором магнитной индукции 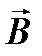. Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности:

.

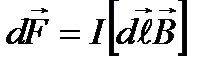9. Сила взаимодействия параллельных проводов с током:

,

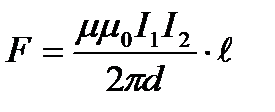где d– расстояние между проводами.

10. Магнитный момент контура с током:

,

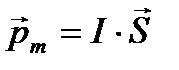где I – сила тока, протекающего по контуру; S – площадь контура; вектор 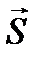численно равен площади S контура и совпадает по направлению с вектором нормали к плоскости контура.

11. Механический (вращательный) момент, действующий на контур с током, помещённый в однородное магнитное поле:

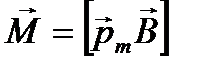, или ,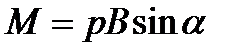

где 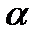− угол между векторам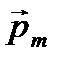и и .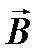

12. Потенциальная энергия контура с током в магнитном поле:

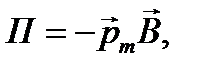или .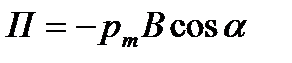

За нулевое значение потенциальной энергии контура с током в магнитном поле принято расположение контура, когда вектор 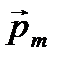перпендикулярен вектору .

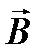13. Отношение магнитного момента 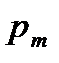к механическому L(моменту импульса) заряженной частицы, движущейся по круговой орбите:

,

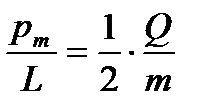где Q – заряд частицы; m – масса частицы.

14. Сила Лоренца:

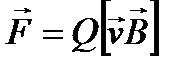, или ,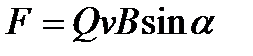

где 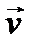− скорость заряженной частицы; 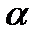− угол между векторам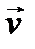и и .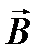

15. Магнитный поток:

а) в случае однородного магнитного поля и плоской поверхности

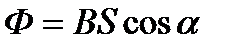, или ,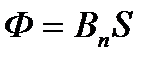

где S – площадь контура; 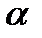− угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности

,

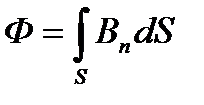интегрирование ведётся по всей поверхности.

16. Потокосцепление (полный поток):

.

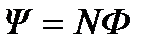Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

17. Работа по перемещению замкнутого контура в магнитном поле:

.

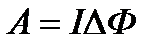18. Э.д.с. индукции:

.

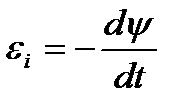19. Разность потенциалов на концах проводника, движущегося со скоростью 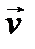в магнитном поле:

,

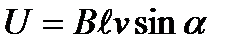где 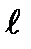− длина проводника; 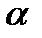− угол между векторам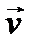и и .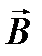

20. Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:

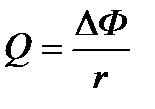, или ,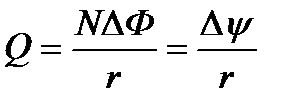

где r – сопротивление контура.

21. Индуктивность контура:

.

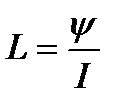22. Э.д.с. самоиндукции:

.

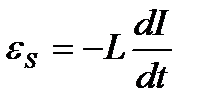Если частица находится одновременно в электрическом и магнитном полях, то под силой Лоренца понимают выражение

.

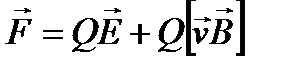23. Индуктивность соленоида:

,

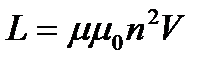где п – число витков, приходящиеся на единицу длины соленоида;

V– объём соленоида.

24. Мгновенное значение силы тока в цепи, обладающей сопротивлением r и индуктивностью L:

а) при замыкании цепи:

,

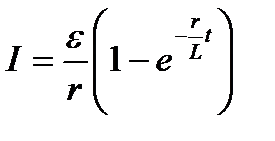где 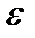− э.д.с. источника тока; t–время, прошедшее после замыкания цепи;

б) при размыкании цепи:

,

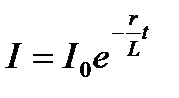где I₀ – значение силы тока в цепи при t=0; t–время, прошедшее с момента размыкания цепи.

25. Энергия магнитного поля:

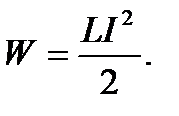
26. Объёмная плотность энергии магнитного поля (энергия, заключенная в единице объёма):

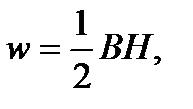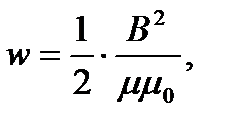или или ,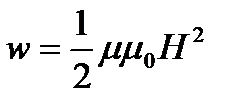

гдеВ – магнитная индукция; Н – напряжённость магнитного поля.

Примеры решения задач

Пример №1.По длинному прямому тонкому проводу течёт ток силой I=12A. Определить магнитную индукциюВ поля, создаваемого проводником в точке, удалённой от него на расстояние r=2см.

L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAEfcbicMA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPT2vCQBTE74LfYXmCN920/mmJrmKLQvAixkKvj+wz Cd19G7JbE799tyB4HGbmN8x621sjbtT62rGCl2kCgrhwuuZSwdflMHkH4QOyRuOYFNzJw3YzHKwx 1a7jM93yUIoIYZ+igiqEJpXSFxVZ9FPXEEfv6lqLIcq2lLrFLsKtka9JspQWa44LFTb0WVHxk/9a BSG7m2PdmZN92+++u9nHImNqlBqP+t0KRKA+PMOPdqYVzGfw/yX+ALn5AwAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEAEfcbicMAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== "/>

по току

I

Решение:

Магнитное поле, создаваемое прямым бесконечно длинным проводником ничтожно малого сечения, обладает осевой симметрией. Это значит, что абсолютная величинаВ магнитной индукции в данной точке будет зависеть

только от её расстояния до проводника. Поэтому все точки на окружности радиуса r (рисунок) лежащей в плоскости, перпендикулярной проводнику, будут иметь одинаковое значение магнитной индукции:

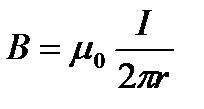, (1)

где 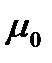− магнитная постоянная.

Направление вектора 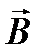зависит от положения точки на окружности и направления тока в проводнике. Этот вектор направлен по касательной к проведённой окружности (это следует из закона Био-Савара-Лапласа, записанного в векторной форме). Линия, касательная к которой в каждой точке совпадает с направлением вектора магнитной индукции, называется магнитной силовой линией. Окружность на рисунке удовлетворяет этому условию, а следовательно, является магнитной силовой линией. Направление магнитной силовой линии, а значит и вектора 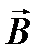определено по правилу правого винта.

В формулу (1) подставим числовые значения величин и произведём вычисления:

.

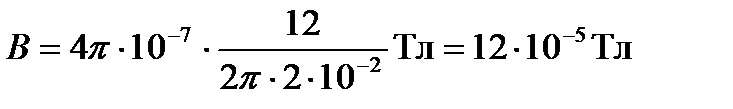Пример №2.По двум параллельным бесконечно длинным проводам DиС, расположенным на расстоянии d=5смдруг от друга, текут в одном направлении токи силой I=50A. Определить магнитную индукцию 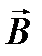поля, создаваемого проводниками с током в точкеА (рисунок), отстоящей от оси одного проводника на расстоянии r₁=3см, от другогоr₂=7см.

Решение:

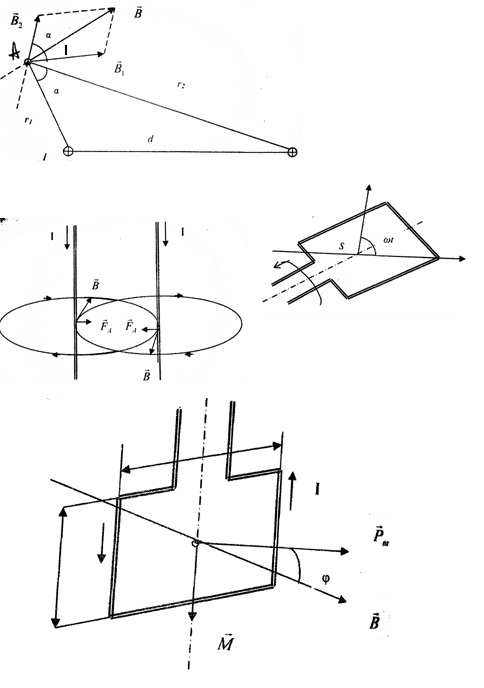Для нахождения магнитной индукции 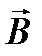в точкеА воспользуемся принципом суперпозиции магнитных полей. Для этого определим направления магнитной индукци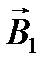и и 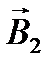полей, создаваемых каждым проводником с током в отдельности и сложим их геометрически: 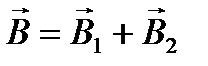. Абсолютное значение магнитной индукцииВможет быть найдено по теореме косинусов:

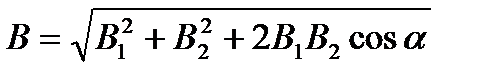, (1)

где 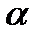− угол между векторам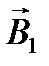и и .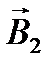

Значения магнитных индукци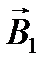й и 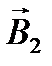выражаются соответственно через силу тока I и расстояния r₁и r₂от проводов до точкиА:

; .

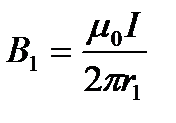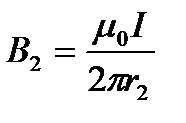Подставляя выражения В₁и В₂ в формулу (1) и вынося 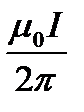за знак корня, получим:

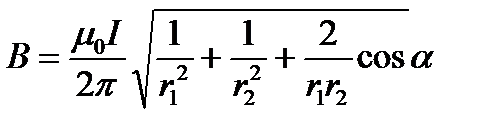. (2)

Вычислим cosα, заметив, что α=ÐDАС (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем:

,

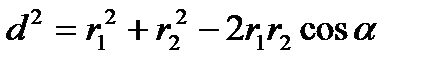где d – расстояние между проводами.

Отсюда .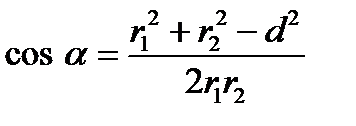

После подстановки числовых значений получим:

.

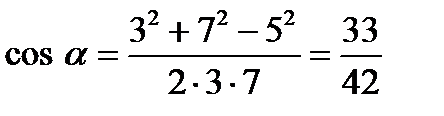Подставляя в формулу (2) значения входящих величин, определяем искомую индукцию:

.

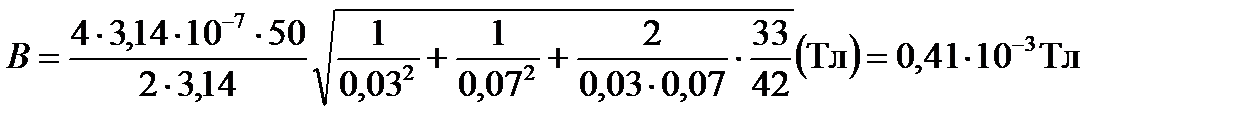Пример №3.По контуру в виде равностороннего треугольника течёт ток силой I=60A. Сторона треугольникаа=25см. Определить магнитную индукцию 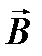в точке пересечения высот (рисунок).

Решение:

D

А

В

I

r0

r0

r0

C

α

Каждый участок проводника с током создаёт в точкеСиндукцию магнитного поля; так как треугольник правильный, то точка С располагается симметрично относительно Д и В; В₁=В₂=В₃.

К

, ,

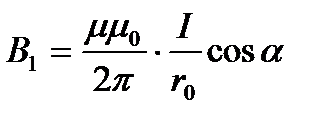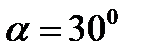где 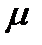− магнитная проницаемость воздуха, равная 1;

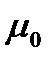− магнитная постоянная, равная ;

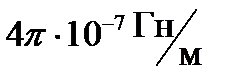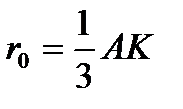; АК=АBcosα;

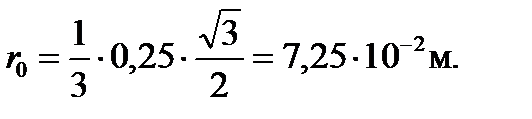
Направление векторов 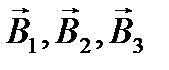определяем по правилу буравчика.

Вектора 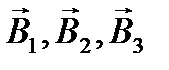имеют одинаковое направление: все они направлены перпендикулярно плоскости чертежа от нас.

В_{от “C”}=3B,

.

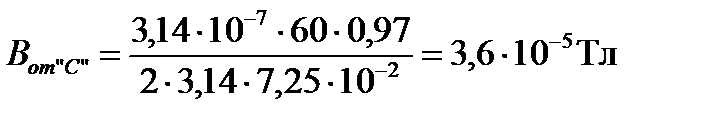Пример №4. По двум параллельным бесконечно длинным проводам, расположенным на расстоянии r=50смдруг от друга, текут токи с одинаковой плотностьюj=2 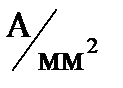. Диаметр каждого проводника

d=0,4мм(рисунок).С какой силой, приходящейся на единицу длины каждого проводника, они притягиваются друг к другу?

Среда – воздух.

Решение:

Индукция магнитного поля каждого прямого проводника с током на расстоянии rот него равна:

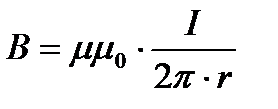, (1)

где 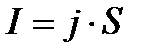− сила тока.

В каждом из двух проводников площадь поперечного сечения равна:

.

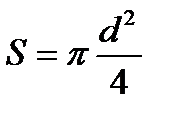С учетом этого:

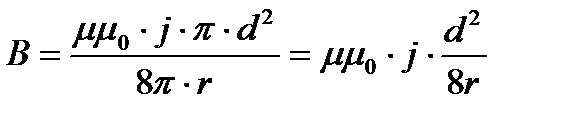. (2)

В этом магнитном поле на второй проводник действует сила Ампера

,

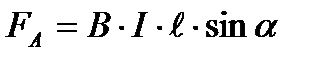где 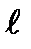− длина проводника; α – угол между направлением тока в проводнике и направлением вектора индукции 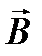магнитного поля.

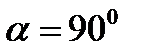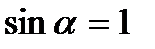Так как , то и 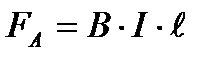, откуда

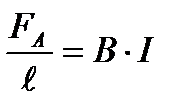. (3)

Подставив (1) и (2) в (3), получим:

.

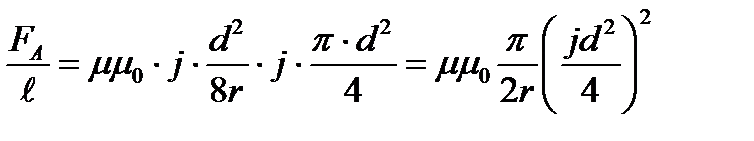Подставим в эту формулу числовые значения физических величин и произведём вычисления:

.

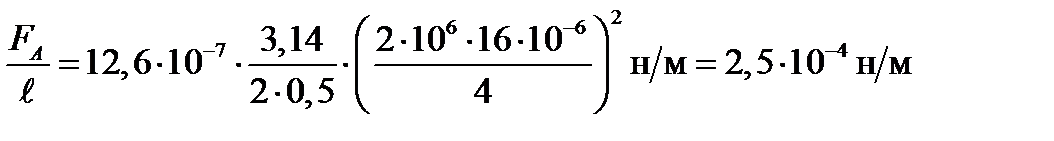Проверим единицу измерения полученной величины:

.

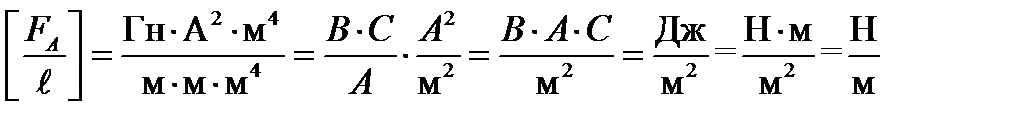Пример №5.Плоский квадратный контур со сторонойа=5см, по которому течёт ток силой I=70A, свободно установился в однородном магнитном поле (В=1Тл) (рисунок). Определить работуА, совершённую внешними силами при повороте контура относительно оси, 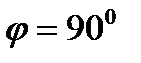. При повороте контура сила тока в нём поддерживается неизменной.

Решение:

На контур с током действует момент сил:

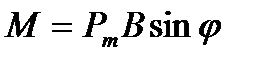, (1)

где 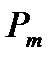− магнитный момент контура; 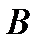− магнитная индукция; 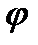− угол между 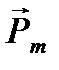и .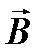

По условию задачи, в начальном положении контур установился в магнитном поле. При этом М=0, значит φ=0, т.е. вектора 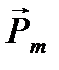и 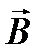совпадают по направлению.

Если внешние силы выведут контур из положения равновесия, то возникший момент сил, определяемый формулой (1), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами

Так как момент сил переменный, то для подсчёта работы применим формулу работы в дифференциальной форме dA=Mdφ. Подставив сюда выражение М по формуле (1) и учтя, что 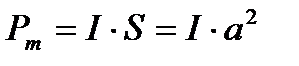, получим:

;

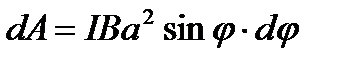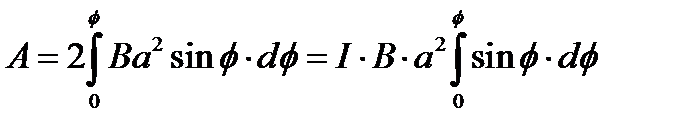. (2)

Работа при повороте на угол :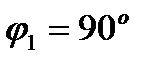

.

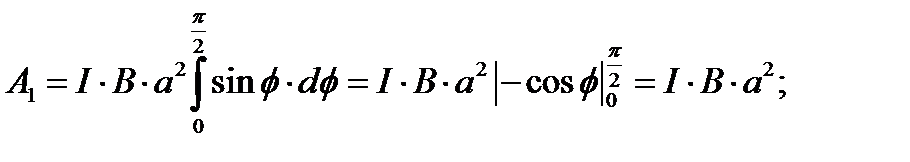
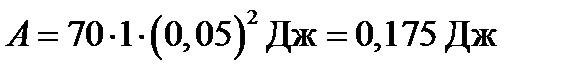Пример №6.Соленоид содержит N=4000 витков провода, по которому течёт ток силой I=20 A (рисунок). Определить магнитный поток Ф и потокосцепление ψ, если индуктивность L=0,4 Гн.

Решение:

Индуктивность связана с потокосцеплением ψ и силой тока соотношением

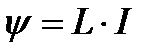. (1)

Потокосцепление, в свою очередь, может быть выражено через поток Ф и число витков N:

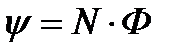. (2)

Из выражений (1) и (2) находим ψ: