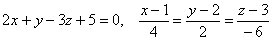Уравнение касательной плоскости и нормали к поверхности

Начнём с базовых вопросов: ЧТО ТАКОЕ касательная плоскость и ЧТО ТАКОЕ нормаль? Многие осознают эти понятия на уровне интуиции. Самая простая модель, приходящая на ум – это шар, на котором лежит тонкая плоская картонка. Картонка расположена максимально близко к сфере и касается её в единственной точке. Кроме того, в точке касания она закреплена торчащей строго вверх иголкой.

В теории существует довольно остроумное определение касательной плоскости. Представьте произвольную поверхность 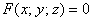и принадлежащую ей точку 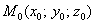. Очевидно, что через точку 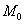проходит много пространственных линий, которые принадлежат данной поверхности. У кого какие ассоциации? =) …лично я представил осьминога. Предположим, что у каждой такой линии существуетпространственная касательная в точке .

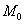Определение 1: касательная плоскость к поверхности в точке 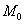– это плоскость, содержащая касательные ко всем кривым, которые принадлежат данной поверхности и проходят через точку .

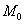Определение 2: нормаль к поверхности в точке 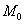– это прямая, проходящая через данную точку перпендикулярно касательной плоскости.

Просто и изящно. Кстати, чтобы вы не померли со скуки от простоты материала, чуть позже я поделюсь с вами одним изящным секретом, который позволяет РАЗ И НАВСЕГДА забыть о зубрёжке различных определений.

С рабочими формулами и алгоритмом решения познакомимся прямо на конкретном примере. В подавляющем большинстве задач требуется составить и уравнение касательной плоскости, и уравнения нормали:

Пример 1

Найти уравнения касательной плоскости и нормали к поверхности 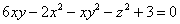в точке .

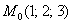Решение:если поверхность задана уравнением 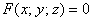(т.е. неявно), то уравнение касательной плоскости к данной поверхности в точке 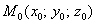можно найти по следующей формуле:

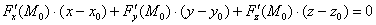
Особое внимание обращаю на необычные частные производные 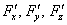– их не следует путать с частными производными неявно заданной функции (хотя поверхность задана неявно). При нахождении этих производных нужно руководствоваться правилами дифференцирования функции трёх переменных, то есть, при дифференцировании по какой-либо переменной, две другие буквы считаются константами:

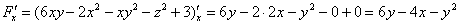
Не отходя от кассы, найдём частную производную в точке:

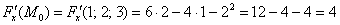
Аналогично:

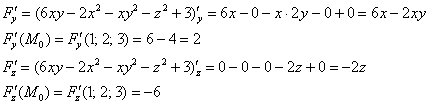
Это был самый неприятный момент решения, в котором ошибка если не допускается, то постоянно мерещится. Тем не менее, здесь существует эффективный приём проверки, о котором я рассказывал на уроке Производная по направлению и градиент.

Все «ингредиенты» найдены и теперь дело за аккуратной подстановкой с дальнейшими упрощениями:

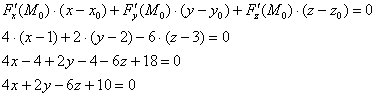
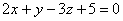– общее уравнение искомой касательной плоскости.

Настоятельно рекомендую проконтролировать и этот этап решения. Сначала нужно убедиться, что координаты точки касания 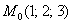действительно удовлетворяют найденному уравнению:

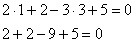
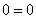– верное равенство.

Теперь «снимаем» коэффициенты 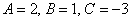общего уравнения плоскости и проверяем их на предмет совпадения либо пропорциональности с соответствующими значениями 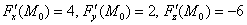. В данном случае пропорциональны. Как вы помните из курса аналитической геометрии, 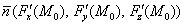– это вектор нормали касательной плоскости, и он же – направляющий вектор нормальной прямой. Составим канонические уравнения нормали по точке 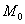и направляющему вектору :

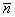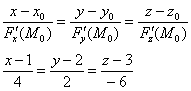
В принципе, знаменатели можно сократить на «двойку», но особой надобности в этом нет

Ответ: