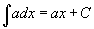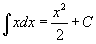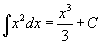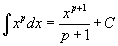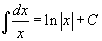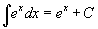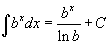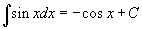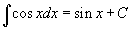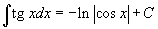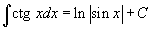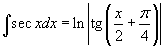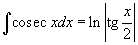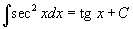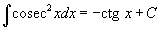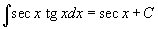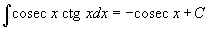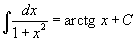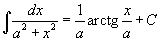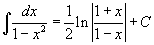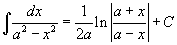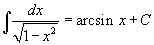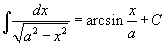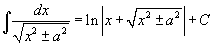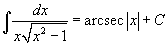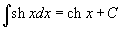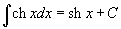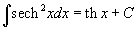Экстремумы функции нескольких переменных
О: Точка 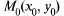 называется точкой максимума (минимума)
называется точкой максимума (минимума)
функции 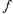 (х, у), если
(х, у), если 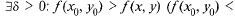
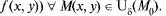
Максимумы и минимумы функции называются ее экстремумами (рис. 12.1).
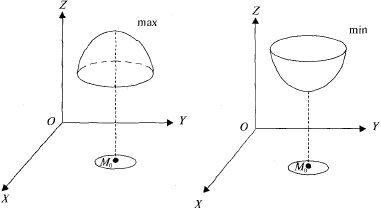
Рис. 12.1
Примеры: 1) 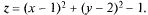
Очевидно т. (1, 2) является т. mm, так как все остальные значения х и у дадут z > -1
2) 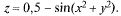 В данном случае т.
В данном случае т. 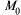 (0, 0) является т. max, так как
(0, 0) является т. max, так как 
Т: (необходимое условие экстремума)
Если функция г = 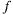 (х,у) имеет экстремум в т.
(х,у) имеет экстремум в т. 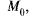 то
то
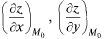 или обращаются в нуль, или не существуют
или обращаются в нуль, или не существуют
Пусть у = 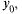 тогда
тогда 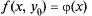 — функция одной переменной. Так как при х =
— функция одной переменной. Так как при х = 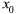 она имеет экстремум, то
она имеет экстремум, то
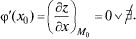
Доказательство при х = 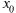 аналогично Эти условия не являются достаточными.
аналогично Эти условия не являются достаточными.
Пример: 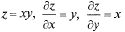 обращаются в нуль в т. О(0,0),
обращаются в нуль в т. О(0,0),
но ху> 0 при х > 0, у > 0, ху< 0 при х < 0, у > 0, т.е. определение экстремума не выполняется.
Приведем достаточные условия экстремума для стационарных
т. 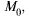 в которых
в которых 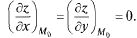
Т: (достаточные условия экстремума) Пусть в некоторой области, содержащей т. 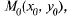 функция
функция 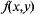 имеет непрерывные частные производные до третьего порядка включительно и эта точка является стационарной.
имеет непрерывные частные производные до третьего порядка включительно и эта точка является стационарной.
Пусть 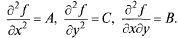
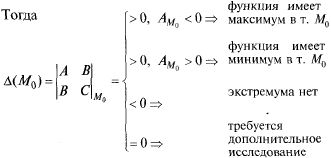
Доказательство см. в [11.С. 419].
Пример: Исследовать на экстремум 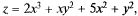
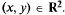
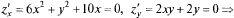
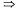
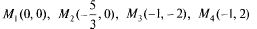 — стационарные точки,
— стационарные точки,
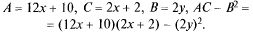
1) 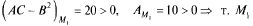 — точка минимума,
— точка минимума,
2)т. 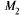 — точка
— точка
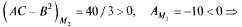 максимума,
максимума,
3) 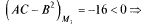 экстремума нет,
экстремума нет,
4) 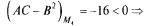 экстремума нет
экстремума нет
Для функции п переменных 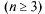 определение экстремума и
определение экстремума и
необходимые условия сохраняются. Необходимое условие в случае дифференцируемой функции 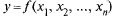 кратко запишется в виде:
кратко запишется в виде: 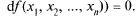
Сформулируем достаточные условия экстремума.
Т: Если в стационарной т. 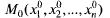 второй дифферен-
второй дифферен-
циал
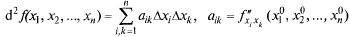
является положительно (отрицательно) определенной квадратичной формой, то 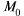 — точка min (max)
— точка min (max)
Доказательство см. в [11.С. 424].
Сформулированные ранее достаточные условия экстремума для функции 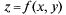 являются следствием данной теоремы
являются следствием данной теоремы
| Неопределенный интеграл и его свойства. Таблица интегралов. | ||||||||||||||||||||||||||||||||
Определение первообразной и неопределенного интеграла Функция F(x) называется первообразной функции f(x), если 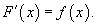 Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функцииf(x) и обозначается как Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функцииf(x) и обозначается как 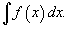 Таким образом, если F - некоторая частная первообразная, то справедливо выражение Таким образом, если F - некоторая частная первообразная, то справедливо выражение 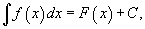 где С - произвольная постоянная. Свойства неопределенного интеграла В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины. · где С - произвольная постоянная. Свойства неопределенного интеграла В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины. · 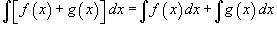 · · 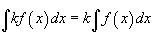 · · 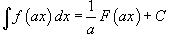 · · 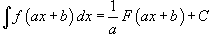 Таблица интегралов В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0). Таблица интегралов В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).
|
| Метод подстановки (замена переменной интегрирования) |
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов: а) 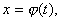 где где 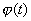 – монотонная, дифференцируемая функция; б) – монотонная, дифференцируемая функция; б) 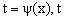 – новая переменная. В первом случае формула замены переменной имеет вид: – новая переменная. В первом случае формула замены переменной имеет вид: 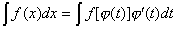 . (6.1) Во втором случае: . (6.1) Во втором случае: 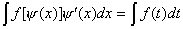 . (6.2) В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой. Пример 12. . (6.2) В обоих случаях после интегрирования следует возвращаться к старой переменной обратной подстановкой. Пример 12. 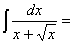 (положим (положим 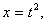 тогда тогда 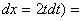 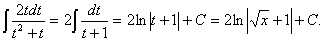 Пример 13. Пример 13. 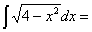 (положим (положим 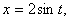 тогда тогда 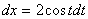 ) = ) = 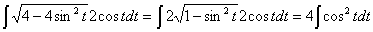 = (используем формулу = (используем формулу 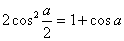 ) = = ) = = 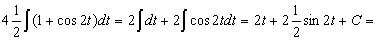 = = 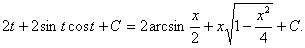 Возвращаясь к старой переменной, использовали выражение: Возвращаясь к старой переменной, использовали выражение: 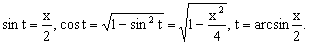 Замечание. В примерах 12 и 13 использовали подстановку вида: Замечание. В примерах 12 и 13 использовали подстановку вида: 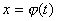 и формулу (6.1). Подстановку и формулу (6.1). Подстановку 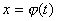 выбирают так, чтобы правая часть формулы (6.1) приобрела более удобный для интегрирования вид. Пример 14. выбирают так, чтобы правая часть формулы (6.1) приобрела более удобный для интегрирования вид. Пример 14. 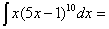 (положим (положим 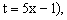 тогда тогда 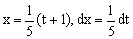 ) = ) = 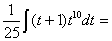 = = 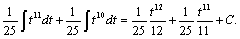 Пример 15. Пример 15. 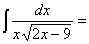 (положим (положим 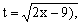 тогда тогда 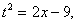 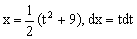 ) = ) = 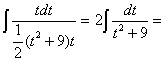 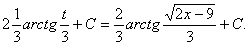 Замечание. Примеры, рассмотренные в п.4 можно было решить методом замены переменной, используя подстановку вида Замечание. Примеры, рассмотренные в п.4 можно было решить методом замены переменной, используя подстановку вида 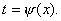 Так, например, Так, например, 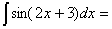 (положим (положим 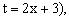 тогда тогда 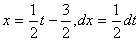 ) = ) = 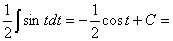 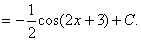 Вычислим Вычислим 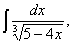 используя подстановку используя подстановку 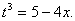 Имеем Имеем 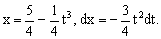 Тогда Тогда 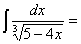 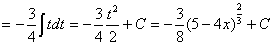 . . |