Эквивалентная схема оэм в осях x-y для установившегося режима работы

Принимаем переменные величины ОЭМ синусоидальными, тогда для установившегося режима работы имеем равенства

,

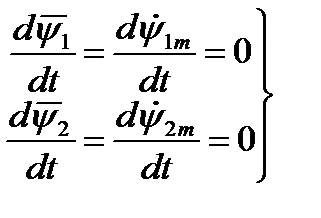где 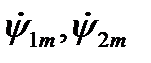- комплексные векторы синусоидальных потокосцеплений статора и ротора.

Для установившегося режима работы комплексно-векторные уравнения (2.142)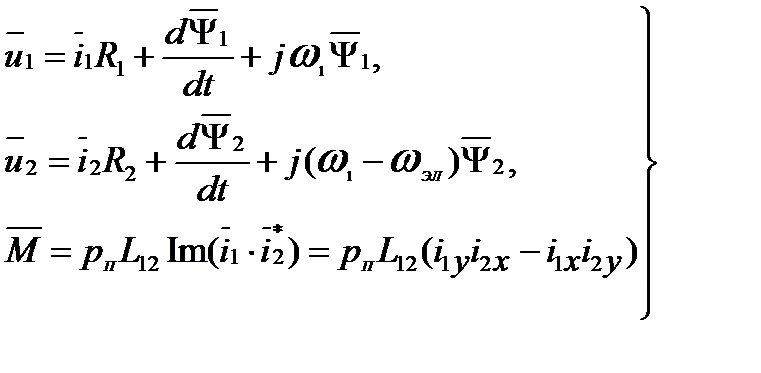

принимают вид:

,

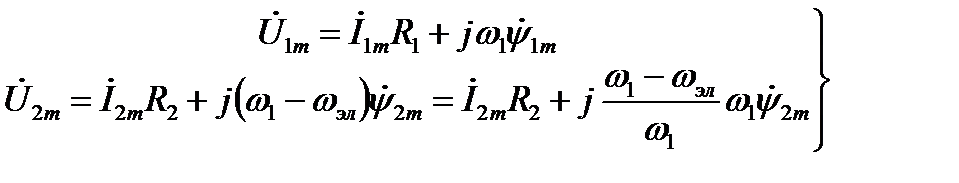где 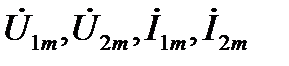- комплексные векторы напряжений и токов статора и ротора ОЭМ.

Отношение 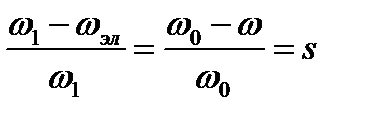, (2.147)

представляет собой скольжение относительно синхронной угловой скорости . Поэтому уравнения электрического равновесия совместно с уравнениями потокосцеплений можно записать таким образом:

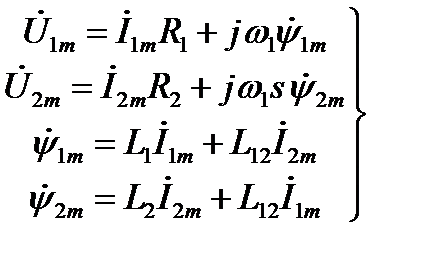, (2.148)

При синусоидальных переменных удобнее перейти от амплитудных к действующим значениям:

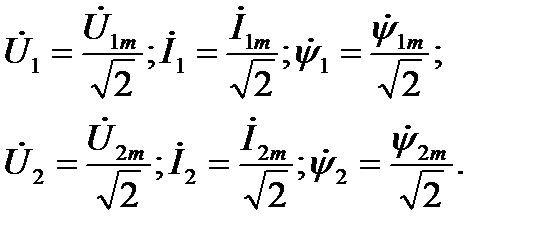
В результате получаем уравнения:

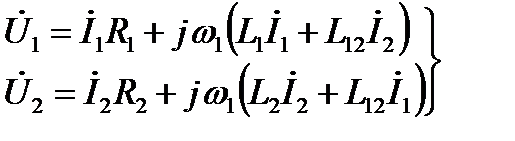, (2.149)

Полагая , разделим второе уравнение (2.149) на , в результате получаем

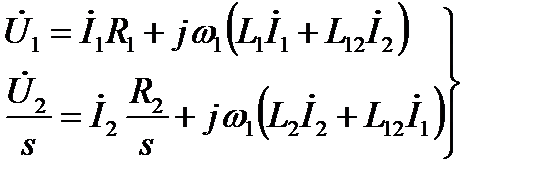, (2.150)

Уравнения (2.150) отличаются от уравнений (2.149) тем, что они описывают процессы при остановленном роторе ( 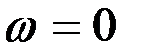), а это значит, что частота переменных ротора и статора одинакова. Инвариантность этого преобразования соблюдается, так как с остановкой ротора электромагнитная энергия не исчезла, а превратилась в эквивалентную энергию, которая выделяется в виде тепла на сопротивлении .

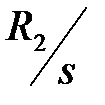Для удобства приведем параметры роторной цепи к параметрам статорной цепи, тогда

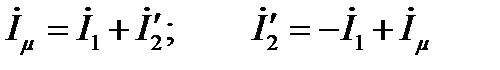, (2.151)

где 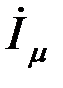- комплекс намагничивающего тока ОЭМ.

Уравнения электрического равновесия (2.150) принимают вид:

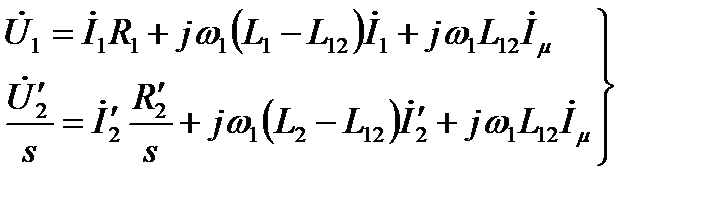, (2.152)

Поскольку

, (2.153)

то

, (2.154)

где - индуктивные сопротивления рассеяния статора, ротора (приведенное) и намагничивающего контура.

Уравнениям (2.154) соответствует эквивалентная схема ОЭМ, показанная на Рис.2.7, причем

(2.155)

- комплекс ЭДС, индуктированной потокосцеплением взаимоиндукции.

ФАЗНЫЕ ПРЕОБРАЗОВАНИЯ ПЕРЕМЕННЫХ

В связи с тем, что большинство электрических машин переменного тока выполняется трехфазными, возникает задача преобразования переменных (напряжений, токов, потокосцеплений) реальной трехфазной машины в переменные двухфазной обобщенной машины. Необходимо также производить и обратные преобразования переменных двухфазной машины в переменные трехфазной машины. При этом все преобразования должны быть инвариантными по мощности.

Рассмотрим сначала преобразование переменных трехфазной электрической машины в переменные двухфазной обобщенной машины. Будем полагать, что переменные и пропорциональны переменным и соответственно. Обозначим коэффициент пропорциональности .

Переменные по осям и могут иметь любую величину, соответственно и по осям .

Совместим ось обмотки статора с осью (Рис.2.8). Отметим углы оси по отношению к осям : и углы оси по отношению к осям : .

В результате можем составить матрицу поворота трехфазных осей к двухфазным:

, (2.156)

Теперь переменные статора двухфазной системы можно выразить через переменные трехфазной системы:

(2.157)

где , (2.158)